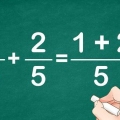Nel nostro esempio, il denominatore della frazione impilata (11/15)/(29/70) è la frazione 29/70. Per trovare l`inverso lo invertiamo e la frazione diventa 70/29. Nota che, se la frazione impilata ha un numero intero al denominatore, puoi trattarla come una frazione e trovare comunque il suo inverso. Ad esempio, supponiamo che la frazione impilata sia (11/15)/(29), quindi possiamo definire il denominatore come 29/1, con il reciproco 1/29. 
Nel nostro esempio moltiplichiamo 11/15 × 70/29. 70 × 11 = 770 e 15 × 29 = 435. Così è la nostra nuova frazione semplice 770/435. 
Un divisore comune di 770 e 435 è 5. Quindi se dividiamo il numeratore e il denominatore della nostra frazione per 5, otteniamo 154/87. 154 e 87 non hanno fattori comuni, quindi sappiamo di aver trovato la risposta finale! 

Questo è più facile da capire con un esempio. Proviamo a semplificare la frazione impilata che abbiamo menzionato sopra, (((1)/(x+3)) + x - 10)/(x +4 +((1)/(x - 5))). I termini di frazione in questa frazione composta sono (1)/(x+3) e (1)/(x-5). Il denominatore comune di queste due frazioni è il prodotto dei loro denominatori: (x+3)(x-5). 
Nel nostro esempio, moltiplichiamo la frazione impilata (((1)/(x+3)) + x - 10)/(x +4 +((1)/(x - 5))), per ((x+ 3 )(x-5))/((x+3)(x-5)). Dovremo moltiplicare per numeratore e denominatore della frazione impilata, moltiplicando ogni termine per (x+3)(x-5). Per prima cosa moltiplichiamo il numeratore: (((1)/(x+3)) + x - 10) × (x+3)(x-5) = (((x+3)(x-5)/(x+3)) + x((x+3)(x-5)) - 10((x+3)(x-5)) = (x-5) + (x(x - 2x - 15)) - (10(x - 2x - 15)) = (x-5) + (x - 2x - 15x) - (10x - 20x - 150) = (x-5) + x - 12x + 5x + 150 = x - 12x + 6x + 145 
Il denominatore della nostra frazione impilata, (((1)/(x+3)) + x - 10)/(x +4 +((1)/(x - 5))), è x +4 +(( 1)/(x-5)). Moltiplichiamo questo per il kgd che abbiamo trovato, (x+3)(x-5). (x +4 +((1)/(x - 5))) × (x+3)(x-5) = x((x+3)(x-5)) + 4((x+3)(x-5)) + (1/(x-5))(x+3)(x-5). = x(x - 2x - 15) + 4(x - 2x - 15) + ((x+3)(x-5))/(x-5) = x - 2x - 15x + 4x - 8x - 60 + (x+3) = x + 2x - 23x - 60 + (x+3) = x + 2x - 22x - 57 
Usando il numeratore e il denominatore che abbiamo trovato sopra, possiamo costruire una frazione uguale alla nostra frazione impilata iniziale, ma non contiene frazioni. Il numeratore che abbiamo ottenuto era x - 12x + 6x + 145 e il denominatore era x + 2x - 22x - 57, quindi la nuova frazione è: (x - 12x + 6x + 145)/(x + 2x - 22x - 57)
Semplifica le frazioni impilate
Contenuto
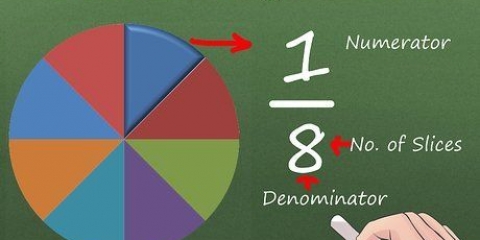
Le frazioni impilate sono quelle in cui il numeratore, il denominatore o entrambi contengono frazioni stesse. Per questo motivo potresti anche chiamarlo `frazioni in frazioni`. La semplificazione delle frazioni impilate è un processo che può variare da facile a difficile in base a quanti termini sono presenti nel numeratore e nel denominatore, se uno qualsiasi dei termini è variabile e, in tal caso, la complessità dei termini variabili. Vedere il passaggio 1 di seguito per iniziare!
Passi
Metodo 1 di 2: semplificazione delle frazioni impilate con la moltiplicazione inversa

1. Se necessario, semplifica il numeratore e il denominatore a poche frazioni. Le frazioni impilate non sono necessariamente difficili da risolvere. In effetti, le frazioni impilate in cui il numeratore e il denominatore contengono entrambi una singola frazione sono generalmente abbastanza facili da risolvere. Quindi, se il numeratore o il denominatore della tua frazione impilata (o entrambi) contiene più frazioni o frazioni e numeri interi, semplifica come desideri per ottenere una singola frazione sia nel numeratore che nel denominatore. Ciò potrebbe richiedere il minimo comune multiplo (LCM) per trovare due o più frazioni.
- Supponiamo di voler semplificare la frazione complessa (3/5 + 2/15)/(5/7 - 3/10). Per prima cosa possiamo quindi semplificare sia il numeratore che il denominatore della nostra frazione complessa in singole frazioni.
- Per semplificare il numeratore, prendiamo un LCF di 15, moltiplicando 3/5 per 3/3. Il nostro contatore diventa 9/15 + 2/15, che equivale a 11/15.
- Per semplificare il denominatore, prendiamo un lcm di 70, moltiplicando 5/7 per 10/10 e 3/10 per 7/7. Il nostro denominatore sarà 50/70 - 21/70, che equivale a 29/70.
- Quindi la nostra nuova frazione impilata lo è (15/11)/(29/70).

2. Capovolgi il denominatore e trova l`inverso. Per definizione, parti da un numero all`altro uguale al moltiplicando il primo numero per il reciproco del secondo. Ora che abbiamo ottenuto una frazione impilata con una singola frazione sia al numeratore che al denominatore, possiamo utilizzare questa proprietà di divisione per semplificare la nostra frazione impilata! Per prima cosa trova il reciproco del denominatore della frazione impilata. Fallo "invertendo" la frazione: il numeratore sostituisce il denominatore e viceversa.

3. Moltiplica il numeratore della frazione impilata per il reciproco del denominatore. Ora che hai ottenuto il reciproco del denominatore della tua frazione impilata, moltiplicalo per il numeratore per ottenere una singola frazione semplice! Ricorda, per moltiplicare due frazioni, non moltiplichiamo in modo incrociato: il numeratore della nuova frazione è il prodotto del numeratore delle due vecchie, e così anche il denominatore.

4. Semplifica la nuova frazione trovando il massimo comun divisore. Ora abbiamo una singola frazione semplice, quindi tutto ciò che resta è rappresentarla nei termini più semplici possibili. Particolare massimo comun divisore (MCD) del numeratore e del denominatore e dividi entrambi per questo numero per semplificare.
Metodo 2 di 2: semplificazione delle frazioni impilate con termini variabili

1. Quando possibile, utilizzare il metodo della moltiplicazione inversa come descritto sopra. Per essere chiari, quasi tutte le frazioni impilate possono essere semplificate riducendo il numeratore e il denominatore a singole frazioni e moltiplicando il numeratore per il reciproco del denominatore. Le frazioni impilate di variabili non fanno eccezione, ma più complicate sono le espressioni delle variabili nella frazione impilata, più è difficile e dispendioso in termini di tempo eseguire la moltiplicazione inversa. Per le frazioni impilate "semplici" con variabili, la moltiplicazione per l`inverso è una buona scelta, ma le frazioni impilate con più termini variabili nel numeratore e nel denominatore possono essere più facili da semplificare utilizzando il metodo alternativo descritto di seguito.
- Ad esempio: (1/x)/(x/6) è facile da semplificare con la moltiplicazione inversa. 1/x × 6/x = `6/x. Non è necessario utilizzare un metodo alternativo.
- Tuttavia, la frazione (((1)/(x+3)) + x - 10)/(x +4 +((1)/(x - 5))) è più difficile da semplificare con la moltiplicazione inversa. Ridurre il numeratore e il denominatore di questa frazione impilata a singole frazioni, moltiplicando inversamente e riducendo il risultato ai termini più semplici, è probabilmente un processo complicato. In questo caso, il metodo alternativo riportato di seguito potrebbe essere più semplice.

2. Se la moltiplicazione inversa non è pratica, inizia trovando il minimo comune divisore dei termini di divisione nella frazione impilata. Il primo passo in questo metodo alternativo di semplificazione è trovare il kgd di tutti i termini frazionari nella frazione impilata, sia al numeratore che al denominatore. Se uno o più termini della frazione hanno variabili al denominatore, il kgd è semplicemente il prodotto dei loro denominatori.

3. Moltiplicare il numeratore della frazione impilata per il kgd appena trovato. Successivamente, dobbiamo moltiplicare i termini nella nostra frazione impilata per il kgd dei termini della sua frazione. In altre parole, moltiplichiamo l`intera frazione impilata per (kgd)/(kgd). Possiamo farlo semplicemente perché (kgd)/(kgd) è uguale a 1. Per prima cosa moltiplica il numeratore per se stesso.

4. Moltiplica il denominatore della frazione impilata per kgd come hai fatto con il numeratore. Moltiplica la frazione impilata per il kgd che hai trovato andando al denominatore. Moltiplica ogni termine per kgd.

5. Forma una nuova frazione semplificata dal numeratore e dal denominatore che hai appena trovato. Dopo aver moltiplicato la tua frazione per la tua espressione (kgd)/(kgd) e averla semplificata cancellando termini simili, dovresti rimanere con una frazione semplice che non contiene termini di frazione. Come avrai notato, i denominatori di queste frazioni si annullano a vicenda (moltiplicando le frazioni nella frazione impilata originale per kgd), lasciando termini variabili e interi nel numeratore e nel denominatore della tua risposta, ma non frazioni.
Consigli
- Mostra ogni fase del tuo lavoro. Le frazioni possono creare confusione se vuoi andare troppo veloce o cercare di toglierle dalla testa.
- Cerca esempi di frazioni impilate online o nel tuo libro di testo. Segui ogni passaggio finché non lo padroneggi.
Articoli sull'argomento "Semplifica le frazioni impilate"
Condividi sui social network:
Popolare