24: 1, 2, 3, 4, 6, 8, 12, 24. 32: 1, 2, 4, 8, 16, 32. Il gcd di 24 e 32 è 8, perché 8 è il numero più grande per cui sia 24 che 32 sono divisibili. 
24/8 = 3 32/8 = 4 Quindi la frazione semplificata è 3/4. 
3 * 8 = 24 4 * 8 = 32 Questa è di nuovo la frazione originale, 24/32. Puoi anche indagare se la frazione non può essere ulteriormente semplificata. Poiché 3 è primo, può essere diviso solo per 1 e per se stesso, quindi questa frazione non può essere ulteriormente semplificata. 

24/2 = 12 32/2 = 16 La nuova frazione semplificata è 12/16. 
12/2 = 6 16/2 = 8 La nuova frazione è 6/8. 
6/2 = 3 8/2 = 4 La nuova frazione sarà 3/4. 
Ad esempio, se vuoi semplificare la frazione 10/40, inizi dividendo numeratore e denominatore per 5, lasciando 2/8. Non puoi dividere di nuovo per 5, ma puoi dividere per 2, rendendo la risposta finale ¼. 
3/4 * 2/2 = 6/8 8/6 * 2/2 = 16/12 16/12 * 2/2 = 32/24. Nota che hai diviso 24/32 per 2 * 2 * 2, che equivale a dividere per 8, il massimo comune divisore di 24 e 32. 

Ad esempio: abbiamo la frazione 24/60. Inizia con 24.Si nota: 24 -- 1, 2, 3, 4, 6, 8, 12, 24 Quindi continua con 60.Si nota: 60 -- 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 
Nel nostro esempio, il numero più grande è il divisore 12. Quindi dividiamo entrambi 24 e 60 per 12, rendendo la frazione 2/5, la nostra frazione semplificata! 

Quindi per 24 hai 2 x 2 x 2 x 3 = 24. E per 60 hai 2 x 2 x 3 x 5 = 60 
Quello che ci resta sono un 2 e un 5 – o 2/5! La stessa risposta che abbiamo ottenuto con il metodo precedente. Se sia il numeratore che il denominatore sono numeri pari, ricorda di dividere il numero a metà. Continua a farlo finché non sono troppo piccoli per dividersi ulteriormente.
Semplificare le frazioni
Contenuto
La matematica non deve essere per forza difficile, ma non è sempre facile ricordare tutti quei principi e metodi diversi. Anche le tecniche di base a volte possono essere dimenticate. Quindi, ecco altri due metodi per semplificare le frazioni.
Passi
Metodo 1 di 4: utilizzo del massimo comun divisore

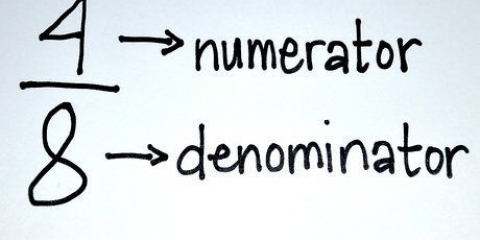
1. Elenca tutti i fattori del numeratore e del denominatore. I fattori di un dato numero sono quei numeri che moltiplicati insieme formano quel numero. Esempio, 3 e 4 sono entrambi fattori di 12, perché 3 x 4 = 12. Per elencare tutti i fattori di un numero, scopri quali numeri vanno fino in fondo in quel numero.
- Elenca i fattori dal più piccolo al più grande e non dimenticare l`1. Questa è la lista:
- 24: 1, 2, 3, 4, 6, 8, 12, 24.
- 32: 1, 2, 4, 8, 16, 32.

2. Trova il massimo comune divisore (gcd) del numeratore e del denominatore. Il gcd è il numero più grande per cui due numeri, in questo caso il numeratore e il denominatore, sono divisibili. Una volta che hai le due liste di fattori pronte, tutto quello che devi fare è trovare il numero più grande (il divisore) che compare in entrambe le liste.

3. Dividi numeratore e denominatore per gcd. Ora che hai trovato il gcd, tutto ciò che devi fare è dividere numeratore e denominatore per questo numero per semplificare il più possibile la tua frazione. Ecco come funziona:

4. Controlla il tuo lavoro. Se vuoi sapere se la tua semplificazione è corretta, moltiplica il numeratore e il denominatore della semplificazione per gcd per assicurarti di ottenere come risultato la frazione originale. Ecco come funziona:
Metodo 2 di 4: continua a dividere per un piccolo numero

1. Scegli un piccolo numero. Usando questo metodo, scegli un numero piccolo, come 2, 3, 4, 5 o 7, per iniziare. Guarda le frazioni per assicurarti che il numero sia divisibile almeno una volta per qualsiasi numero tu scelga. Ad esempio, se prendi la frazione 24/108, non scegliere 5, perché non si adatta a nessuno dei due numeri. Ma se stai studiando la frazione 25/60, allora 5 è un`ottima scelta.
- Nel caso della frazione 24/32, il numero 2 funziona benissimo. Poiché entrambi i numeri sono pari, sono anche divisibili per 2.

2. Dividi il numeratore e il denominatore di una frazione per quel numero per semplificarlo. Ecco come ha funzionato:

3. ripeti questo. Poiché entrambi i numeri sono ancora pari, puoi continuare a dividere per 2. Se uno dei due numeri diventa dispari, prova a usare un altro numero come divisore. Ecco come va avanti:

4. Continua a dividere per 2 finché non puoi andare oltre.

5. Assicurati che la frazione non possa essere ulteriormente semplificata. Come nell`esempio precedente: 3 è primo e quindi ¾ non può essere ulteriormente semplificato. Se il numeratore e il denominatore di una frazione non possono essere nuovamente divisi per il numero scelto, provare con un altro numero.

6. Controlla la tua risposta. Ritorna al punto di partenza moltiplicando 3/4 per 2/2 tre volte e controlla se la risposta è uguale a 24/32. Qui potete vedere questo elaborato:
Metodo 3 di 4: elenca i divisori

1. Scrivi la tua frazione. Lascia un ampio spazio sul lato destro del foglio: si tratta di annotare i fattori.

2. Elenca i fattori del numeratore e del denominatore. Mettili in elenchi separati. Potrebbe essere più semplice se gli elenchi sono allineati uno sopra l`altro. Inizia con 1 e poi vai dal più piccolo al più grande e scrivi le coppie.

3. Trova il massimo comun divisore (gcd).Qual è il numero più grande che è sia un divisore del numeratore che del denominatore?? Qualunque cosa sia, dividi entrambi i numeri per quel numero.
Metodo 4 di 4: Utilizzo di fattori primi

1. Trova i fattori primi del numeratore e del denominatore. UN "numero primo" è un numero che non può essere diviso per nessun altro intero tranne 1 e se stesso. 2, 3, 5, 7 e 11 sono esempi di numeri primi.
- Inizia con il contatore. Dividi 24 nei fattori 2 e 12. poiché 2 è un numero primo, hai finito immediatamente con quel ramo! Ora dividi 12 nei fattori 2 e 6. 2 è primo -- bene! Ora dividi il 6 nei fattori 2 e 3. Ora hai 2, 2, 2 e 3 come numeri primi.
- Continua con il denominatore. Dividi 60 nei fattori 2 e 30. Dividi 30 nei fattori 2 e 15. Dividi 15 in 3 e 5, entrambi primi. Ora hai il seguente elenco di numeri primi: 2, 2, 3 e 5.

2. Scrivi i fattori primi del numeratore e del denominatore. Prendi la serie di numeri primi che hai trovato moltiplicali insieme. Fallo per numeratore e denominatore. Questo rende più facile vedere cosa sta succedendo.

3. Ignora i fattori uguali. È possibile rimuovere qualsiasi coppia di numeri di entrambe le serie. In questo caso abbiamo due coppie di due e una coppia di tre. Quelli possono essere rimossi!
Consigli
- Se hai domande, chiedi al tuo insegnante; questo probabilmente può aiutarti.
Articoli sull'argomento "Semplificare le frazioni"
Condividi sui social network:
Popolare