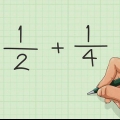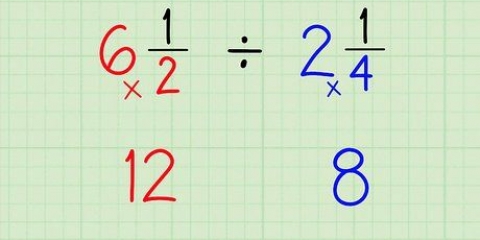Aggiungi e Sottrai Frazioni

Contenuto

Passi

L`aggiunta e la sottrazione di frazioni è un`abilità essenziale da apprendere. Ti imbatti in frazioni ovunque nella vita di tutti i giorni, specialmente a lezione di matematica, dalla scuola primaria all`università. Basta seguire i passaggi seguenti per imparare come aggiungere e sottrarre frazioni se sono frazioni uguali, disuguali, miste o improprie. Una volta che hai imparato un modo, tutto il resto è molto più semplice!

Passi

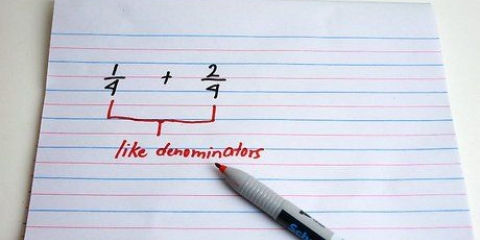
Metodo 1 di 3: addizione e sottrazione di frazioni con lo stesso denominatore

Immagine intitolata Aggiungi e sottrai frazioni Step 1

1. Scrivi l`equazione. Se il denominatore delle due frazioni che aggiungi/sottrai è lo stesso, includi anche questo denominatore nella tua risposta.

In altre parole, non devi scrivere 1/5 e 2/5 come 1/5 + 2/5 = ? Questo può essere notato come (1+2)/5 = ?. Il denominatore è lo stesso e quindi deve essere menzionato solo una volta. Entrambi i numeratori sono sopra la linea del punteggio.

Immagine titolata Aggiungi e sottrai frazioni Step 2

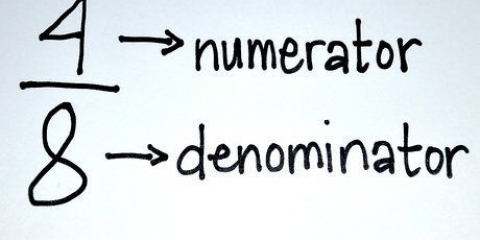
2. Aggiungi i contatori insieme. Il numeratore è il numero sopra la linea di frazione. Prendi il seguente esempio: 1/5 e 2/5; ecco 1 e 2 i nostri contatori.

Sia che tu scriva 1/5 + 2/5 o 1+2/5, la risposta è la stessa: 3! Infine, 1 + 2 = 3.

Immagine titolata Aggiungi e sottrai frazioni Step 3

3. Lascia invariato il denominatore. Niente da aggiungere, sottrarre, ecc, ma invariato.

Quindi, seguendo lo stesso esempio, il denominatore è 5. È tutto! Questo è il numero più basso della frazione e metà della risposta!

Immagine titolata Aggiungi e sottrai frazioni Step 4

4. Scrivi la risposta. Ora non ti resta che scrivere la risposta! Vedrai che secondo l`esempio precedente, la risposta è 3/5.

Qual era il contatore? 3. E il denominatore? 5. Quindi, 1/5 + 2/5, o 1+2/5, è uguale 3/5.

Metodo 2 di 3: addizione e sottrazione di frazioni con denominatori diversi

Immagine titolata Aggiungi e sottrai frazioni Step 5

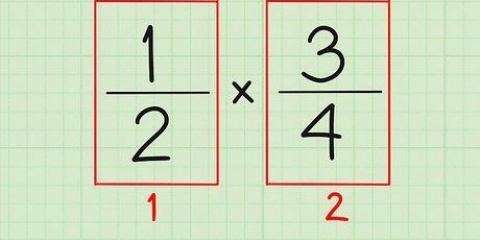
1. Trova il minimo comune multiplo (LCM) dei denominatori. Questo è il numero più piccolo che entrambi i denominatori hanno in comune. Prendi le frazioni 2/3 e 3/4. Quali sono i denominatori? 3 e 4. Per trovare l`LCF di entrambi, utilizzare uno dei seguenti 3 modi:

Annota i multipli. I multipli di 3 sono 3, 6, 9, 12, 15, 18...e così via. I multipli di 4? 4, 8, 12, 16, 20, ecc. Qual è il numero più basso che si verifica in entrambi i set?? 12! Questo è il tuo multiplo minimo comune o il tuo kgv.
Fattorizzazione in fattori primi. Se sai cosa sono i fattori primi, puoi usare la fattorizzazione. Qui determini con quali numeri primi puoi moltiplicare un certo numero mediante moltiplicazione "produrre". Per 3, i fattori sono 3 e 1. Per 4, i fattori primi sono 2 e 2. Quindi moltiplichi questi insieme, quindi 3 x 2 x 2 = 12. il tuo kgf!

Moltiplica entrambi i numeri per ottenere ilpoco numeri. In alcuni casi, come questo, puoi semplicemente moltiplicare entrambi i numeri insieme – 3 x 4 = 12. Ma se i tuoi denominatori sono numeri grandi, questo non può semplicemente accadere! Non puoi semplicemente fare 56 x 44 e passare a 2464 come risposta! Non è sbagliato, ma è imbarazzante.

Immagine titolata Aggiungi e sottrai frazioni Step 6

2. moltiplica il denominatore per il numero che ti serve per ottenere lcg. In altre parole, vuoi che ogni denominatore sia lo stesso numero: il kgv. Per il nostro esempio, questo deve essere 12. 4 x 3 = 12. Questo è il denominatore della nostra risposta finale.

Quindi 2/3 diventa 2/3 x 4 e 3/4 diventa 3/4 x 3. Ciò significa che ora abbiamo 2/12 e 3/12. Ma non abbiamo ancora finito!

Noterai che in questo caso i denominatori sono stati moltiplicati insieme. Funziona in questa situazione, ma non sempre. A volte dovrai cercare numeri più piccoli per trovare l`LCF.

E in altri casi, con numeri piccoli, tutto ciò che devi fare è moltiplicare insieme i denominatori.

Immagine titolata Aggiungi e sottrai frazioni Step 7

3. Moltiplica anche il numeratore per quel numero. Se moltiplichi il denominatore di una frazione per un numero, dovrai moltiplicare anche il numeratore per lo stesso numero. Quello che abbiamo fatto nell`ultimo passaggio è stato solo una parte della moltiplicazione necessaria.

Avevamo 2/3x4 e 3/4x3 come primo passaggio: per aggiungere il secondo passaggio è in realtà 2 x 4/3 x 4 e 3 x 3/4 x 3. Ciò significa che 8/12 e 9/12 sono i nostri nuovi numeri. Perfetto!

Immagine titolata Aggiungi e sottrai frazioni Step 8

4. Aggiungi (o sottrai) i numeratori per ottenere la tua risposta. Per sommare 8/12 a 9/12, basta sommare i numeratori. Non dimenticare: lasci in pace il denominatore. Il numero che hai ottenuto con l`LCF è il tuo denominatore finale.

In questo esempio vale: 8+9/12 = 17/12. Per convertirlo in un numero misto, sottrai il denominatore dal numeratore e guarda cosa ti rimane. Cioè, in questo caso, 17/12 = 1 5/12

Metodo 3 di 3: addizione e sottrazione di frazioni miste e improprie

Immagine titolata Aggiungi e sottrai frazioni Step 9

1. Converti le tue frazioni miste in frazioni improprie. Una frazione mista è un numero intero seguito da una frazione, come nell`esempio sopra (1 5/12). Una frazione impropria è una frazione con un numeratore maggiore del denominatore. Un esempio di questo è 17/12.

Come esempio prendiamo 13/12 e 17/8.

Immagine intitolata Aggiungi e sottrai frazioni Step 10

2. Trova il denominatore comune. Ricorda i tre modi per trovare l`lcg dei denominatori? Determinando i multipli, utilizzando fattori primi o moltiplicando insieme i denominatori.

Determiniamo quali sono i multipli di 12 e 8. Qual è il numero più piccolo in cui rientrano entrambi i numeri?? 24. 8, 16, 24 e 12, 24 – bingo!

Immagine titolata Aggiungi e sottrai frazioni Step 11

3. Moltiplica i numeratori per i denominatori per ottenere la frazione uguale. Entrambi i denominatori devono ora essere convertiti in 24. Come fare 24 di 12? Moltiplicalo per 2. Dalle 8 alle 24? Moltiplicalo per 3. Ma non dimenticare che devi anche moltiplicare i numeratori!

Quindi 13 x 2/12 x 2 = 26/24. E 17 x 3/8 x 3 = 51/24. Abbiamo fatto molta strada per risolvere il problema!

Immagine titolata Aggiungi e sottrai frazioni Step 12

4. Somma e sottrazione di frazioni. Ora che entrambe le frazioni hanno lo stesso denominatore, puoi facilmente sommare o sottrarre entrambe le frazioni. Ricorda, lascia stare il denominatore!

26/24 + 51/24 = 77/24. Questa è la pausa che stavi cercando! Ma il bancone è abbastanza grande....

Immagine titolata Aggiungi e sottrai frazioni Step 13

5. Trasforma la tua risposta in una frazione mista. Un numeratore così grande è un po` strano e rende difficile avere un`idea della dimensione della tua frazione. Tutto quello che devi fare per risolvere è dividere il numeratore per il denominatore e usare il resto come numeratore per la tua nuova frazione composta.

Per questo esempio: 24 va in 77. 3 volte.Quindi, 24 x 3 = 72. Quindi rimane un resto di 5! Allora qual è la tua risposta finale? 3 5/24. È tutto!