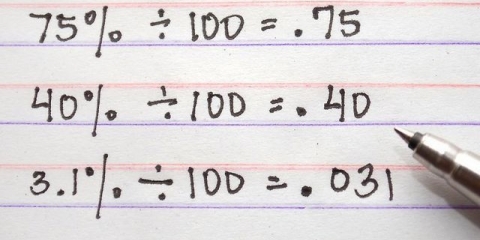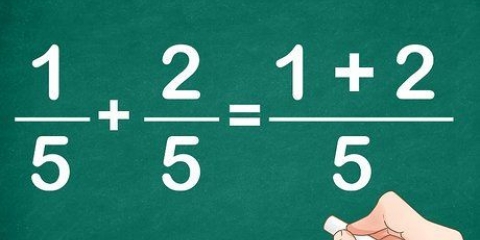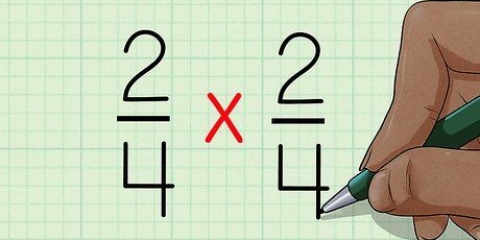Quindi supponiamo di avere 1/2 x 3/4, quindi moltiplichiamo come segue: 1 x 3 e 2 x 4.La risposta è quindi 3/8. 


Se il problema era 8/15 ÷ 3/4, ora questo sarà 8/15 x 4/3. 
8 x 4 = 32 e 15 x 3 = 45, quindi la risposta è 32/45. 

Nel nostro esempio questo diventa: 3 x 5 = 15.

Nel nostro esempio: 15 + 2 = 17 
Nel nostro caso questo diventa: 17/5. 

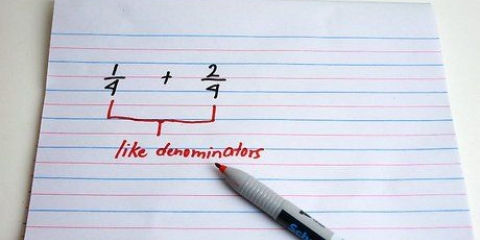
Determina quante volte il denominatore presente va nel minimo comune multiplo. Per 1/4, 4 x 3 = 12. Per 1/6, 6 x 2 = 12. Moltiplica il numeratore e il denominatore della frazione per quel numero. Per ¼, moltiplichi sia 1 che 4 per 3, ottenendo 3/12. 1/6 x 2 = 2/12. Ora questa affermazione è simile a questa: 3/12 + 2/12 o 3/12 - 2/12. 
Quindi per 3/12 + 2/12 la risposta è 5/12. Per il 3/12 - 2/12, è 1/12 Converti le frazioni miste in frazioni improprie prima di iniziare. Chiedi al tuo insegnante se dovresti semplificare o meno le risposte. Ad esempio, 2/5 non può essere ulteriormente semplificato, ma 16/40 sì.
Risolvere le frazioni
Contenuto
Le frazioni a volte sembrano un po` difficili da risolvere, ma con un po` di pratica e qualche conoscenza in più diventa molto più facile. Una volta comprese le basi, scoprirai che risolvere le frazioni è in realtà un gioco da ragazzi.
Passi
Metodo 1 di 4: moltiplicazione delle frazioni

1. Assicurati di avere a che fare con due frazioni. Queste istruzioni funzionano solo con due frazioni.Se hai a che fare con una frazione mista, convertila prima in una frazione impropria...

2. Moltiplica il numeratore 1 per il numeratore 2 e moltiplica il denominatore 1 per il denominatore 2.
Metodo 2 di 4: Dividere le frazioni

1. Assicurati di avere a che fare con due frazioni. Ancora una volta, questo processo funziona SOLO se hai convertito le frazioni miste in frazioni improprie.

2. Invertire la seconda frazione. Non importa quale frazione, a patto di non invertire entrambe le frazioni.

3. Cambia il segno di divisione in una moltiplicazione.

4. Moltiplica entrambi i numeratori ed entrambi i denominatori.
Metodo 3 di 4: Conversione di frazioni miste in frazioni improprie

1. Converti le frazioni miste in frazioni improprie. Le frazioni improprie sono quelle frazioni il cui numeratore è maggiore del denominatore.(Ad esempio, 17/5.) Se stai moltiplicando e dividendo, devi convertire le frazioni miste in frazioni improprie prima di continuare a risolvere il problema.
- Supponiamo di avere la frazione mista 3 2/5.

2. Prendi il numero intero (il numero prima della frazione) e moltiplicalo per il denominatore.


3. Aggiungi quella risposta al contatore.

4. Metti questo numero come nuovo numeratore sopra la linea di frazione e avrai una frazione impropria.
Metodo 4 di 4: addizione e sottrazione di frazioni

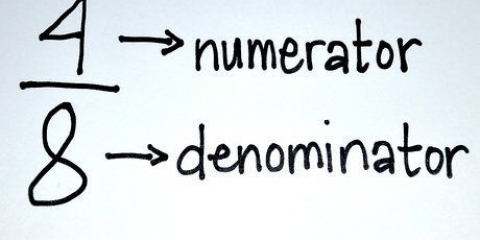
1. Trova il minimo comune multiplo dei denominatori (il numero in basso). Sia per l`aggiunta che per la sottrazione di frazioni, inizi con lo stesso. Trova il numero più piccolo che combacia con entrambi i denominatori.
- Ad esempio, se prendi le frazioni 1/4 e 1/6, il minimo comune multiplo è 12. (4x3=12, 6x2=12)

2. Moltiplica le frazioni in base al multiplo minimo comune. Ricorda, non stai cambiando la frazione, ma solo come viene espressa. Pensa a una pizza: 1/2 o 2/4 di una pizza sono la stessa quantità di pizza, solo espressa in modo diverso.

3. Somma o sottrai i due numeratori (numero superiore) ma NON i denominatori.Questo non è consentito perché vuoi calcolare quanto di questa frazione hai in totale. Se includi anche i denominatori, le frazioni cambieranno.
Consigli
- Assicurati di padroneggiare bene le abilità matematiche di base (addizioni, sottrazioni, moltiplicazioni e divisioni), in modo che i calcoli non richiedano troppo tempo e siano difficili.
- Il reciproco di un intero sta mettendo quel numero come denominatore in una frazione, con un 1 come numeratore. Ad esempio, 5 diventa 1/5.
- Puoi moltiplicare e dividere frazioni miste senza prima convertirle in frazioni improprie. Ma poi hai bisogno di altre abilità matematiche e il calcolo diventa molto più complesso. Quindi è generalmente meglio seguire il percorso delle frazioni improprie.
- Ricorda: dividere equivale a moltiplicare per il reciproco.
- Quando prendi l`inverso di un numero negativo, il segno meno rimane al numeratore.
Avvertenze
- Chiedi al tuo insegnante se devi convertire le frazioni improprie in frazioni miste.
- Ad esempio, 3 1/4 invece di 13/4.
Articoli sull'argomento "Risolvere le frazioni"
Condividi sui social network:
Popolare