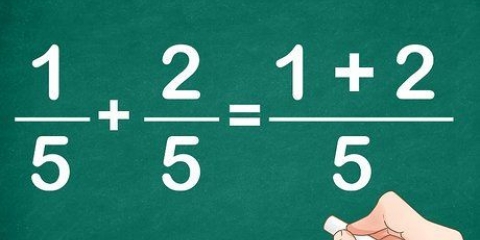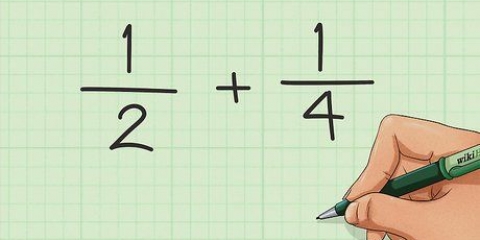La tua risposta è una frazione composta dal nuovo numeratore e dal nuovo denominatore. La tua risposta è 4/16. 
4/4 = 1 16/4 = 4 La nuova frazione e la risposta finale sono 1/4. 

2/2 = 1 4/2 = 2 La nuova frazione è 1/2. È equivalente a 2/4, il che significa che ha lo stesso valore. Puoi anche trovare il numero più grande di cui il numeratore e il denominatore sono divisibili determinando il massimo comune divisore (gcd) di entrambi i numeri. Per fare ciò, elenca semplicemente tutti i fattori di quei numeri e scegli il numero più grande per cui entrambi sono divisibili. Lo fai come segue: 2: 1, 2. 4: 1, 2, 4. 2 è il numero più grande che rientra sia in 2 che in 4. 
2/4 = 1/2 
1 * 1 = 1. 
2 * 2 = 4. 
1/2 * 1/2 = 1/4.
Moltiplica le frazioni
Contenuto
Moltiplicare le frazioni è una delle abilità di base che chiunque abbia a che fare con le frazioni dovrebbe conoscere. Per moltiplicare le frazioni, moltiplica insieme i numeratori e i denominatori, quindi semplifica la risposta (se possibile). Con un po` di pratica chiunque può imparare a moltiplicare le frazioni come un vero matematico.
Passi
Metodo 1 di 2: Moltiplica e poi semplifica

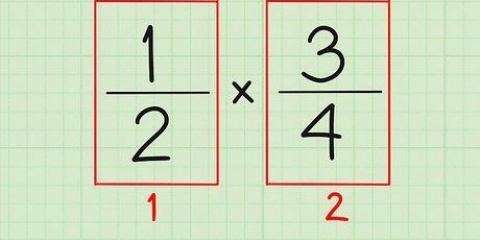
1. Nota il compito. Le due frazioni dovrebbero essere scritte in modo che i numeratori siano allineati con i loro denominatori.
- Per esempio.: 2/4 * 2/4

2. Moltiplica i numeratori delle due frazioni. Poiché i numeratori sono entrambi 2, moltiplica 2 * 2 = 4.

3. Moltiplica i denominatori delle due frazioni. Poiché i denominatori sono entrambi 4, moltiplica 4 * 4 = 16.

4. Semplificare. Per semplificare una frazione, dividi il numeratore e il denominatore per il numero più grande che rientri in entrambi i numeri. A 4/16, 4 è il numero più grande che si adatta a entrambi i numeri, quindi dividi sia il numeratore che il denominatore per 4. Lo fai come segue:
Metodo 2 di 2: semplifica e poi moltiplica

1. Scrivi il compito. I numeratori e denominatori delle due frazioni dovrebbero essere in fila.
- Per esempio.: 2/4 * 2/4

2. Semplifica la prima frazione. Per semplificare la prima frazione, 2/4, dividi numeratore e denominatore per il numero più grande che rientra in entrambi. Questo numero è 2, quindi dividi 2 e 4 per 2. Lo fai come segue:

3. Semplifica la seconda frazione. Per completare questa procedura non devi far altro che semplificare la seconda frazione proprio come la prima. Poiché la seconda frazione, 2/4, è uguale alla prima, anche la tua risposta sarà la stessa.

4. Moltiplica i numeratori di entrambe le frazioni. Moltiplica i numeratori delle frazioni 1/2 e 1/2, quindi 1 e 1.

5. Moltiplica i denominatori di entrambe le frazioni. Moltiplica i denominatori delle frazioni 1/2 e 1/2, quindi 2 e 2.

6. Posiziona il nuovo numeratore sopra il nuovo denominatore. Dato che hai già fatto la semplificazione all`inizio del problema, hai trovato la risposta finale.
Consigli
- a moltiplicando un numero intero per una frazione, scrivi il problema come una frazione con 1 al denominatore (es., se vuoi moltiplicare 36, scrivi questo come 36/1) e moltiplica ulteriormente come indicato sopra.
- Sebbene le frazioni vengano tradizionalmente moltiplicate moltiplicando i numeratori e poi i denominatori, puoi anche moltiplicare prima i denominatori senza modificare la risposta.
- Moltiplicando un numero per un numero inferiore a 1, il prodotto sarà più piccolo di entrambi i numeri nella moltiplicazione.
Articoli sull'argomento "Moltiplica le frazioni"
Condividi sui social network:
Popolare