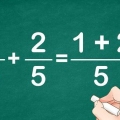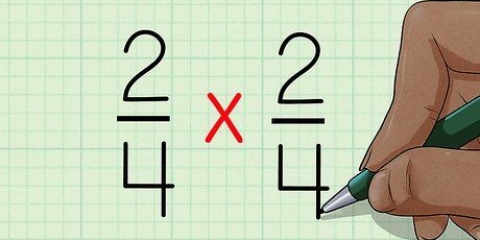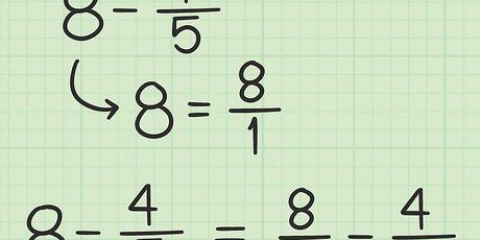(/2) = /2 × /2 o (/2). Al quadrato di ogni numero si ottiene (/4). 
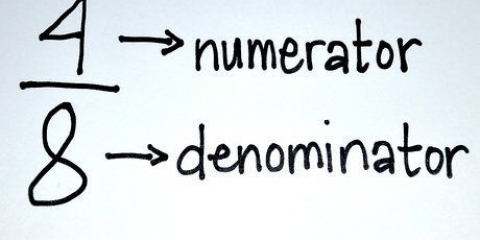
Il numeratore sta sopra la frazione e il denominatore sta in basso. Ad esempio: (/2) = (/2x2) = (/4). 
Per convertirlo in un numero misto, dividi 25 per 4. Questo è 6 (6 x 4 = 24), con un resto di 1. Pertanto, il numero misto è 6/4. 

Ad esempio: (-/4) = (–/4) X (-/4) 
Ad esempio: (-2) x (-8) = (+16) 
Continuando con l`esempio, la frazione risultante sarà un numero positivo. (–/4) X (-/4) = (+/16) L`usanza è di omettere il segno più dai numeri positivi. 
Ad esempio: (/16) ha un fattore comune di quattro. Dividi la frazione per 4: 4/4 = 1, 16/4= 4 Riscrivi la frazione semplificata: (/4) 

Ad esempio: 16 × (/16) Al quadrato le parentesi ed elimina il fattore comune di 16: 16 * /16 * /16 Dato che hai a che fare qui con un 16 come intero e due volte un 16 al denominatore, puoi eliminarne uno. Riscrivi l`equazione semplificata: 12 × /16 semplificare /16 dividendo per 4: /4 Moltiplica: 12 × /4 = 36/4 Parte: 36/4 = 9 
Ad esempio: 16 * (/16) Riscrivi con numeratore e denominatore al quadrato: 16 * (/16) Sottrarre l`esponente al denominatore: 16 * /16 Immagina i primi 16 come esponenti di 1:16. Usando le regole per la sottrazione di potenze/esponenti, sottrai gli esponenti l`uno dall`altro. 16/16, dà 16 = 16 o 1/16. Ora procedi con /16 Riscrivi e semplifica la frazione: /16 =* /4. Semplifica: 12 × /4 = 36/4 Parte: 36/4 = 9
Frazioni al quadrato
Contenuto
La quadratura delle frazioni è una delle operazioni più semplici che puoi eseguire sulle frazioni. È molto simile alla quadratura di interi in quanto puoi semplicemente moltiplicare sia il numeratore che il denominatore per se stessi. Ci sono alcuni casi in cui la semplificazione della frazione prima della quadratura rende la procedura più semplice. Se non hai ancora appreso questa abilità, questo articolo fornisce una breve panoramica per migliorare la tua comprensione.
Passi
Parte 1 di 3: quadratura delle frazioni

1. Impara come quadrare gli interi. Quando vedi un numero elevato alla seconda potenza, sai di quadrare il numero. Questo equivale a moltiplicare il numero per se stesso. Ad esempio:
- 5 = 5 × 5 = 25

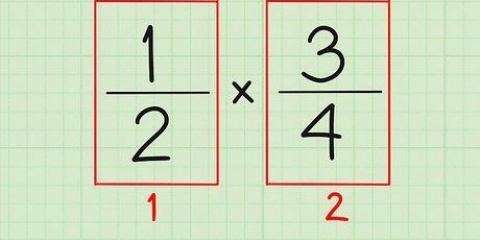
2. Ti rendi conto di quella quadraturafrazioni funziona allo stesso modo. Per quadrare una frazione, moltiplica la frazione per se stessa. Un altro modo per pensare a questo è moltiplicare il numeratore per se stesso e il denominatore per se stesso. Ad esempio:

3. Moltiplica il numeratore per se stesso e il denominatore per se stesso. L`ordine effettivo in cui moltiplichi questi numeri per se stessi non ha importanza, a patto di quadrare entrambi i numeri. Per semplificare le cose, inizia con il numeratore: basta moltiplicarlo per se stesso. Quindi moltiplica il denominatore per se stesso.

4.Semplificare la frazione per concludere. Quando si tratta di frazioni, l`ultimo passaggio è sempre semplificare la frazione nella sua forma più semplice o convertire una frazione impropria in un numero misto. Il nostro esempio, /4 è una frazione impropria perché il numeratore è maggiore del denominatore.
Parte 2 di 3: quadratura delle frazioni con numeri negativi

1. Cerca un segno meno davanti alla frazione. Se hai a che fare con una frazione negativa, c`è un segno meno davanti ad essa. È consigliabile mettere sempre le parentesi attorno a un numero negativo in modo da sapere che il segno meno si riferisce al numero e non è inteso come una somma negativa.
- Ad esempio: (-/4)

2. Moltiplica la frazione per se stessa. Quadra la frazione come faresti normalmente, moltiplicando il numeratore per se stesso e poi moltiplicando il denominatore per se stesso. Puoi anche semplicemente moltiplicare la frazione per se stessa.

3. Comprendi che moltiplicando insieme due numeri negativi si ottiene un numero positivo. Quando è presente un segno meno, l`intera frazione diventa negativa. Quando elevi al quadrato la frazione, moltiplichi due numeri negativi. Quando due numeri negativi vengono moltiplicati insieme, il prodotto è sempre positivo.

4. Rimuovere il segno meno dopo la quadratura. Se hai quadrato la frazione, hai moltiplicato due numeri negativi. Ciò significa che la frazione al quadrato è positiva. Non dimenticare di omettere il segno meno nella risposta finale.

5. Semplifica il più possibile la frazione. Il passaggio finale per eseguire i calcoli delle frazioni è semplificare. Le frazioni improprie devono prima essere semplificate a numeri misti e poi ulteriormente semplificate.
Parte 3 di 3: Utilizzo di semplificazioni e soluzioni rapide

1. Controlla se riesci a fare la frazionesemplificare prima di piazzarlo. Di solito è più facile semplificare le frazioni prima della quadratura. Ricorda, per semplificare una frazione devi dividerla per un fattore comune fino a quando 1 è l`unico numero rimasto che può essere diviso sia per il numeratore che per il denominatore. Semplificare prima una frazione significa che non devi semplificarla di nuovo alla fine, quando i numeri sono più grandi.
- Ad esempio: (/16)
- 12 e 16 possono essere divisi entrambi per 4. 12/4 = 3 e 16/4 = 4; così puoi/16 semplificare a /4.
- Ora puoi fare la frazione /4 al quadrato.
- (/4) = /16, che non puoi più semplificare.
- Per dimostrarlo, rendiamo al quadrato la frazione originale senza semplificare:
- (/16) = (/16x16) = (/256)
- (/256) ha un fattore comune di 16. Dividendo sia il numeratore che il denominatore per 16 semplifica la frazione in (/16), la stessa frazione che abbiamo ottenuto semplificando prima.

2. Impara quando evitare di semplificare una frazione. Hai a che fare con più complessi equazioni, allora potrebbe essere possibile eliminare uno dei fattori. In tal caso è quindi più conveniente attendere semplificando la frazione. L`aggiunta di un fattore aggiuntivo all`esempio sopra lo rende più chiaro.

3. Comprendi come farlo rapidamente con ilesponente. Un altro modo per risolvere lo stesso problema è innanzitutto semplificare l`esponente. Il risultato sarà lo stesso, ottenuto solo attraverso un percorso diverso.
Necessità
- Carta o computer
- Matita/penna (se si utilizza la carta)
Articoli sull'argomento "Frazioni al quadrato"
Condividi sui social network:
Popolare