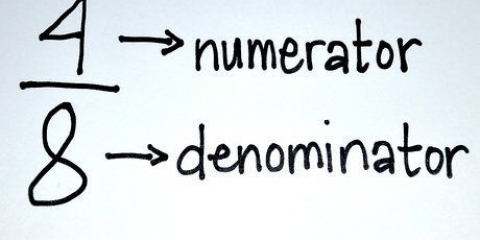
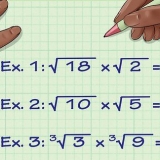Risolvere Equazioni Trigonometriche: 8 Passaggi (con Immagini)

Un`equazione trigonometrica è un`equazione con una o più funzioni trigonometriche della curva trigonometrica variabile x. Risolvere per x significa trovare i valori delle curve trigonometriche le cui funzioni trigonometriche rendono vera l`equazione trigonometrica.

Risposte o valori delle curve di soluzione, sono espressi in gradi o radianti. Esempi:

x = Pi/3 ; x = 5Pi/6 ; x = 3Pi/2 ; x = 45 gradi; x = 37,12 gradi; x = 178,37 gradi

Nota: sul cerchio unitario, le funzioni trigonometriche di qualsiasi curva sono uguali alle funzioni trigonometriche dell`angolo corrispondente. Il cerchio unitario definisce tutte le funzioni trigonometriche della variabile curva x. Viene anche usato come prova quando si risolvono equazioni e disuguaglianze trigonometriche di base.
Esempi di equazioni trigonometriche:

sin x + sin 2x = 1/2; tan x + lettino x = 1.732;
cos 3x + sin 2x = cos x; 2sin 2x + cos x = 1 .

Il cerchio unitario.
Questo è un cerchio con Raggio = 1, dove O è l`origine. Il cerchio unitario definisce 4 funzioni principali trigonometriche della variabile curva x, che ruota attorno ad essa in senso antiorario.
Quando la curva di valore x varia sulla circonferenza unitaria, vale:
L`asse orizzontale OAx definisce la funzione trigonometrica f(x) = cos x.
L`asse verticale OBy definisce la funzione trigonometrica f(x) = sin x.
L`asse verticale AT definisce la funzione trigonometrica f(x) = tan x.
L`asse orizzontale BU definisce la funzione trigonometrica f(x) = lettino x.

Il cerchio unitario viene utilizzato anche per risolvere equazioni trigonometriche di base e disuguaglianze trigonometriche standard, considerando le varie posizioni della curva x sul cerchio.

Passi

Immagine titolata Risolvi le equazioni trigonometriche Step 1

1. Comprendi il metodo di soluzione.

Per risolvere un`equazione trigonometrica, convertila in una o più equazioni trigonometriche di base. La risoluzione di equazioni trigonometriche alla fine porta a risolvere 4 equazioni trigonometriche di base.

Immagine titolata Risolvi le equazioni trigonometriche Step 2

2. Saper risolvere le equazioni trigonometriche di base.

Esistono 4 equazioni trigonometriche di base:

peccato x = a; cos x = a

abbronzatura x = a; lettino x = a

La risoluzione delle equazioni trigonometriche di base avviene studiando le varie posizioni della curva x sul cerchio trigonometrico e utilizzando una tabella di conversione trigonometrica (o calcolatrice). Per comprendere appieno come risolvere queste e simili equazioni trigonometriche di base, leggi il seguente libro:"Trigonometria: risoluzione di equazioni trigonometriche e disuguaglianze" (Ebook Amazon 2010).

Esempio 1. Risolvi per sin x = 0,866. La tabella di conversione (o calcolatrice) fornisce la risposta: x = Pi/3. Il cerchio trigonometrico fornisce un`altra curva (2Pi/3) con lo stesso valore per il seno (0,866). Il cerchio trigonometrico fornisce anche un`infinità di risposte chiamate risposte estese.

x1 = Pi/3 + 2k.Pi e x2 = 2Pi/3.(Risposte entro un periodo (0, 2Pi))

x1 = Pi/3 + 2k Pi e x2 = 2Pi/3 + 2k Pi.(Risposte dettagliate).

Esempio 2. Risolvi: cos x = -1/2. Le calcolatrici danno x = 2 Pi/3. Il cerchio trigonometrico fornisce anche x = -2Pi/3.

x1 = 2Pi/3 + 2k.Pi e x2 = - 2Pi/3.(Risposte per il periodo (0, 2Pi))

x1 = 2Pi/3 + 2k Pi e x2 = -2Pi/3 + 2k.pi.(Risposte dettagliate)

Esempio 3. Risolvi: tan (x - Pi/4) = 0.

x = Pi/4 ;(Risposta)

x = Pi/4 + k Pi;(Risposta estesa)

Esempio 4. Risolvi: lettino 2x = 1.732. Le calcolatrici e il cerchio trigonometrico danno:

x = Pi/12 ;(Risposta)

x = Pi/12 + k Pi ;(Risposte dettagliate)

Immagine titolata Risolvi le equazioni trigonometriche Step 3

3. Impara le trasformazioni usate per risolvere le equazioni trigonometriche.

Per convertire una data equazione trigonometrica in equazioni trigonometriche standard, utilizzare le conversioni algebriche standard (fattorizzare, fattore comune, polinomi...), definizioni e proprietà delle funzioni trigonometriche e delle identità trigonometriche. Sono circa 31, di cui 14 identità trigonometriche, da 19 a 31, dette anche identità detrasformate, perché utilizzate nella conversione di equazioni trigonometriche. Vedi il libro sopra.

Esempio 5: L`equazione trigonometrica: sin x + sin 2x + sin 3x = 0 può essere convertita in un prodotto di equazioni trigonometriche di base utilizzando identità trigonometriche: 4cos x*sin (3x/2)*cos (x/2) = 0. Le equazioni trigonometriche di base da risolvere sono: cos x = 0 ; sin(3x/2) = 0 ; e cos(x/2) = 0.

Immagine titolata Risolvi le equazioni trigonometriche Step 4

4. Trova le curve di cui si conoscono le funzioni trigonometriche.

Prima di poter imparare a risolvere le equazioni trigonometriche, devi sapere come trovare rapidamente le curve le cui funzioni trigonometriche sono note. I valori di conversione delle curve (o angoli) possono essere determinati con tabelle trigonometriche o calcolatrice.

Esempio: risolvere per cos x = 0.732. La calcolatrice fornisce la soluzione x = 42,95 gradi. Il cerchio unitario fornisce altre curve con lo stesso valore per il coseno.

Immagine titolata Risolvi le equazioni trigonometriche Step 5

5. Disegna l`arco della risposta sul cerchio unitario.

Puoi creare un grafico per illustrare la soluzione del cerchio unitario. I punti finali di queste curve sono costituiti da normali poligoni sul cerchio trigonometrico. Qualche esempio:

I punti finali della curva x = Pi/3 + k.Pi/2 è un quadrato sulla circonferenza unitaria.

Le curve di x = Pi/4 + k.Pi/3 sono rappresentati dalle coordinate di un esagono sul cerchio unitario.

Immagine titolata Risolvi le equazioni trigonometriche Step 6

6. Impara a risolvere le equazioni trigonometriche.

Se l`equazione trigonometrica data contiene solo una funzione trigonometrica, risolvila come un`equazione trigonometrica standard. Se l`equazione data contiene due o più funzioni trigonometriche, allora ci sono 2 metodi di soluzione a seconda delle opzioni per convertire l`equazione.

un.Metodo 1.

Converti l`equazione trigonometrica in un prodotto della forma: f(x).g(x) = 0 o f(x).g(x).h(x) = 0, dove f(x), g(x) e h(x) sono equazioni trigonometriche di base.

Esempio 6. Risolvi: 2cos x + sin 2x = 0.(0 < X < 2Pi)

Soluzione. Sostituisci sin 2x nell`equazione usando l`identità: sin 2x = 2*sin x*cos x.

cos x + 2*peccato x*cos x = 2cos x*( sin x + 1)= 0. Quindi risolvi 2 funzioni trigonometriche standard: cos x = 0 e (sin x + 1) = 0.

Esempio 7. Risolvi: cos x + cos 2x + cos 3x = 0.(0 < X < 2Pi)

Soluzione: convertilo in un prodotto, utilizzando le identità trigonometriche: cos 2x(2cos x + 1 ) = 0. Ora risolvi le 2 equazioni trigonometriche di base: cos 2x = 0 e (2cos x + 1) = 0.

Esempio 8. Risolvi: sin x - sin 3x = cos 2x.(0 < X < 2Pi)

Soluzione: convertilo in un prodotto, utilizzando le identità trigonometriche: -cos 2x*(2sin x + 1) = 0. Ora risolvi le 2 equazioni trigonometriche di base: cos 2x = 0 e (2sin x + 1) = 0.

B.Approccio 2.

Converti l`equazione trigonometrica in un`equazione trigonometrica con una sola funzione trigonometrica univoca come variabile. Ci sono alcuni suggerimenti su come scegliere una variabile adatta. Le variabili comuni sono: sin x = t; cos x = t; cos 2x = t, tan x = t e tan (x/2) = t.

Esempio 9. Risolvi: 3peccato^2 x - 2cos^2 x = 4peccato x + 7(0 < X < 2Pi).

Soluzione. Nell`equazione, sostituisci (cos^2 x) con (1 - sin^2 x) e semplifica l`equazione:

3peccato^2 x - 2 + 2peccato^2 x - 4peccato x - 7 = 0. Ora usa sin x = t. L`equazione diventa: 5t^2 - 4t - 9 = 0. Questa è un`equazione quadratica con 2 radici: t1 = -1 e t2 = 9/5. Possiamo rifiutare il secondo t2 perché > 1. Ora risolvi per: t = sin = -1 --> x = 3Pi/2.

Esempio 10. Risolvi: tan x + 2 tan^2 x = lettino x + 2.

Soluzione. Usa tan x = t. Converti l`equazione data in un`equazione con t come variabile: (2t + 1)(t^2 - 1) = 0. Risolvi per t da questo prodotto, quindi risolvi l`equazione trigonometrica standard tan x = t per x.

Immagine titolata Risolvi le equazioni trigonometriche Step 7

7. Risolvi equazioni trigonometriche speciali.

Ci sono alcune equazioni trigonometriche speciali che richiedono alcune conversioni specifiche. Esempi:

a*peccato x+ b*cos x = c ; a(peccato x + cos x) + b*cos x*peccato x = c ;

a*peccato^2 x + b*peccato x*cos x + c*cos^2 x = 0

Immagine titolata Risolvi le equazioni trigonometriche Step 8

8. Impara le proprietà periodiche delle funzioni trigonometriche.

Tutte le funzioni trigonometriche sono periodiche, nel senso che ritornano allo stesso valore dopo una rotazione su un periodo. Esempi:

La funzione f(x) = sin x ha 2Pi come periodo.

La funzione f(x) = tan x ha Pi come periodo.

La funzione f(x) = sin 2x ha Pi come periodo.

La funzione f(x) = cos (x/2) ha 4Pi come periodo.

Se il periodo è specificato negli esercizi/test, devi solo trovare la/e curva/e x all`interno di questo periodo.

ATTENZIONE: Risolvere equazioni trigonometriche è complicato e spesso porta a errori ed errori. Pertanto le risposte dovrebbero essere controllate attentamente. Dopo aver risolto è possibile verificare le risposte utilizzando una calcolatrice grafica, per una rappresentazione diretta dell`equazione trigonometrica data R(x) = 0. Le risposte (come radice quadrata) sono date in decimali. Ad esempio, Pi ha un valore di 3,14