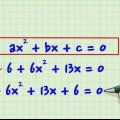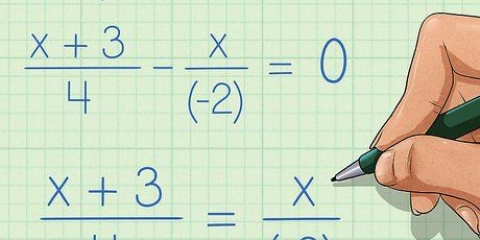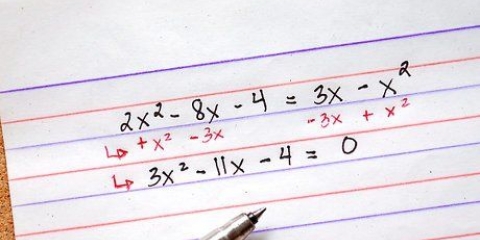Ad esempio, la variabile 12y può essere riscritta come il prodotto dei fattori di 12 e y. Possiamo scrivere 12y come 3(4y), 2(6y), ecc., utilizzando i fattori di 12 che sono più convenienti. Possiamo anche arrivare fino a 12 anni parecchie volte sciogliere. In altre parole, non dobbiamo fermarci a 3(4y) o 2(6y) - possiamo calcolare 4y e 6y in 3(2(2y) e 2(3(2y) rispettivamente). Apparentemente queste due espressioni si equivalgono. 
Proviamo un problema di esempio. Per fattorizzare l`equazione 12x + 6, cerchiamo prima il gcd di 12x e 6. 6 è il numero più grande che divide sia 12x che 6, quindi possiamo semplificare l`equazione in 6(2x + 1). Questo processo si applica anche alle equazioni che coinvolgono numeri e frazioni negativi. x/2 + 4, ad esempio, può essere semplificato in 1/2(x + 8) e -7x + -21 può essere scomposto in -7(x + 3). 

Ad esempio, prendi l`equazione quadratica x + 5x + 6 = 0. Poiché 3 x 2 = 6 e 3 + 2 = 5, l`equazione semplificata diventa (x + 3)(x + 2). Lievi variazioni su questa semplice soluzione rapida possono essere trovate nell`equazione stessa: Se l`equazione quadratica è nella forma x-bx+c, la tua risposta sarà simile a questa: (x - _)(x - _). Se della forma x+bx+c, la tua risposta sarà simile a questa: (x + _)(x + _). Se della forma x-bx-c, la tua risposta sarà simile a questa: (x + _)(x - _). Nota: gli spazi vuoti possono essere frazioni o decimali. Ad esempio, l`equazione x + (21/2)x + 5 = 0 fattori in (x + 10)(x + 1/2). 
Elaboriamo un compito di esempio. 3x - 8x + 4 sembra un po` intimidatorio all`inizio. Ma se ci rendiamo conto che 3 ha solo due fattori (3 e 1), allora diventa molto più facile, perché sappiamo che la nostra risposta deve essere della forma (3x +/- _)(x +/- _). In questo caso, inserendo -2 negli spazi vuoti si otterrà la risposta corretta. -2 × 3x = -6x e -2 × x = -2x. -6x + -2x = -8x. -2 × -2 = 4, quindi vediamo che i termini calcolati tra parentesi moltiplicati insieme, hanno l`equazione originale come prodotto. 
Ad esempio, l`equazione x + 6x + 9 soddisfa questa forma. 3 fa 9 e 3 × 2 fa 6. Quindi sappiamo che i fattori di questa equazione sono uguali a (x + 3)(x + 3) o (x + 3). 
Torniamo all`equazione x + 5x + 6 = 0. L`equazione risolta è (x + 3)(x + 2) = 0. Se uno di questi fattori è uguale a 0, l`intera equazione è 0, quindi le possibili risposte per x sono quei numeri in cui (x + 3) e (x + 2) sono uguali a 0. Questi numeri sono rispettivamente -3 e -2. 
Applichiamo -2 e -3 a x + 5x + 6 = 0. Primo: -2: (-2) + 5(-2) + 6 = 0 4 + -10 + 6 = 0 0 = 0. Questo è corretto, quindi -2 è una risposta valida. Ora proviamo -3: (-3) + 5(-3) + 6 = 0 9 + -15 + 6 = 0 0 = 0. Anche questo è corretto, quindi -3 è anche una risposta valida. 

L`equazione 4x + 8xy + 4y può essere riscritta come 4x + (2 × 2 × 2)xy + 4y. Ora diventa chiaro che è nella forma corretta, quindi possiamo affermare con una certa sicurezza che la nostra equazione può essere scomposta in (2x + 2y). 
Ad esempio: 8x - 27y possono essere calcolati in (2x - 3y)(4x + ((2x)(3y)) + 9y).
Equazioni fattorizzanti
Contenuto
In matematica lo è fattorizzare determinare numeri o espressioni che, quando moltiplicati insieme, producono un valore o un`equazione particolare. Il factoring è un`abilità utile da apprendere quando si risolvono semplici problemi di matematica; la capacità di fattorizzare correttamente diventa quasi essenziale quando si tratta di equazioni quadratiche e altri polinomi. Il factoring può essere utilizzato per semplificare semplici equazioni matematiche per risolverle più facilmente. Il factoring può permetterti di escludere tu stesso possibili risposte molto più velocemente che se dovessi controllare ognuna di esse.
Passi
Metodo 1 di 3: Fattorizzazione di numeri ed equazioni semplici

1. Comprendere la definizione di factoring in numeri. Il factoring è semplice in linea di principio, ma in pratica può essere piuttosto impegnativo quando si risolvono equazioni complesse. Pertanto, l`approccio più semplice è iniziare con numeri piccoli e poi semplici equazioni prima di passare ad applicazioni più avanzate. Il fattori di un dato numero sono i numeri che, moltiplicati tra loro, danno quel singolo numero. Ad esempio, i fattori di 12 sono 1, 12, 2, 6, 3 e 4, perché 1 × 12, 2 × 6 e 3 × 4 hanno tutti 12 come prodotto.
- Un altro modo di pensare a questo è che i fattori di un dato numero sono quei numeri che compongono il numero può essere condiviso nella sua interezza.
- Riesci a trovare tutti i fattori di 60? Usiamo il numero 60 per varie applicazioni (il numero di minuti in un`ora, secondi in un minuto, ecc.) perché è divisibile per un grande insieme di numeri.
- I fattori di 60 sono 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 e 60.

2. Comprendere che le equazioni possono anche essere fattorizzate. Proprio come i numeri, anche le variabili con coefficienti possono essere fattorizzate. Lo fai trovando i fattori del coefficiente della variabile. Sapere come fattorizzare le variabili è utile per semplificare le equazioni di cui fanno parte le variabili.

3. Applicare la proprietà distributiva della moltiplicazione alla fattorizzazione di equazioni matematiche. Utilizzando la tua conoscenza di come fattorizzare sia i numeri regolari che le variabili con i coefficienti, puoi anche semplificare le equazioni matematiche determinando i fattori comuni ai numeri e alle variabili in un`equazione matematica. Di solito semplificheremo l`equazione il più possibile, cercando il massimo comun divisore (gcd). Questo processo di semplificazione è possibile grazie alla proprietà distributiva della moltiplicazione, che afferma che per qualsiasi numero a, b e c, a(b + c) = ab + ac.
Metodo 2 di 3: Fattorizzazione di equazioni di secondo grado

1. Assicurati che l`equazione sia in forma quadratica (ax + bx + c = 0). le equazioni quadratiche sono della forma ax + bx + c = 0, dove a, b e c sono costanti numeriche e a non è uguale a 0 (notare che a è uguale a potere sono su 1 o -1). Se hai a che fare con un`equazione con una variabile (x) e uno o più termini di x al quadrato, di solito puoi scambiare i termini dell`equazione usando un`operazione matematica standard per ottenere 0 su un lato dell`equazione. segno e ascia, ecc. d`altro canto.
- Ad esempio, hai la seguente equazione matematica: 5x + 7x - 9 = 4x + x - 18 che può essere semplificata in x + 6x + 9 = 0, nella forma quadratica.
- Equazioni con potenze maggiori di x, come x, x, ecc. non sono equazioni quadratiche. Queste sono equazioni cubiche o superiori, a meno che l`equazione non possa essere semplificata in modo da eliminare i termini con potenze maggiori di x(rispetto ai quadrati).

2. Nelle equazioni quadratiche in cui a = 1, si calcola in (x+d )(x+e), dove d × e = c e d + e = b. Se la tua equazione quadratica è nella forma x + bx + c = 0 (in altre parole, se il coefficiente di x = 1), allora è possibile (ma non certo) che una scorciatoia relativamente semplice possa essere utilizzata per fattorizzare l`equazione. Trova due numeri che hanno entrambi c come prodotto e sommali insieme per ottenere b come somma. Se hai questi due numeri d ed e, inseriscili nella seguente espressione: (x+d)(x+e). Questi due termini, quando moltiplicati, ti danno l`equazione quadratica - in altre parole, sono i fattori della tua equazione quadratica.

3. Se possibile puoi anche dissolvere i fattori semplicemente osservando da vicino. Che tu ci creda o no, puoi risolvere semplici equazioni quadratiche semplicemente osservando attentamente il problema e poi soppesando le possibili risposte fino a trovare quella giusta. In altre parole, scomponi in fattori provando. Se l`equazione è della forma ax+bx+c e a>1, allora i termini saranno della forma (dx +/- _)(ex +/- _), dove d ed e sono costanti maggiori di zero che moltiplicate tra loro hanno come prodotto. Sia d che e (o entrambi) potere uguale a 1, ma non è sempre così. Se entrambi sono 1, allora hai essenzialmente utilizzato il metodo rapido descritto sopra.

4. Risolvilo quadrando. In alcuni casi le equazioni quadratiche possono essere fattorizzate rapidamente e facilmente utilizzando una speciale proprietà matematica. Qualsiasi equazione quadratica della forma x + 2xh + h = (x + h). Quindi se nella tua equazione il valore di b è il doppio di quello della radice quadrata di c, allora la tua equazione può essere scomposta in (x + (sqrt(c))).

5. Usa i fattori per risolvere le equazioni quadratiche. Indipendentemente da come si fattorizza un`equazione quadratica; una volta calcolato, puoi trovare le possibili risposte per il valore di x impostando ogni fattore uguale a zero e risolvendolo. Dal momento che stai cercando valori per x dove la tua equazione è zero, un valore per x che rende uno dei due fattori uguale a zero sarà la possibile risposta della tua equazione quadratica.

6. Controlla le tue risposte: alcune di esse potrebbero non essere corrette! Una volta trovate le possibili risposte per x, riapplicale all`equazione originale per vedere se sono valide. A volte le risposte che trovi saranno l`equazione originale non rendi uguale a zero quando li applichi. Queste risposte sono errato e li ignoriamo.
Metodo 3 di 3: Fattorizzazione di altre forme di equazioni

1. Se l`equazione è della forma a-b, allora i termini fattorizzati sono (a+b)(a-b). Le equazioni di due variabili vengono risolte in modo diverso rispetto alle equazioni quadratiche. Per ogni equazione a-b dove a e b non sono uguali a 0, i fattori dell`equazione sono (a+b)(a-b).
- Ad esempio, l`equazione 9x - 4y = (3x + 2y)(3x - 2y).

2. Se l`equazione è della forma a+2ab+b, scomponila in(a+b). Nota: per a il trinomio della forma a-2ab+b, la forma disciolta è leggermente diversa: (a-b).

3. Se l`equazione è della forma a-b, allora la scomponi in (a-b)(a+ab+b). Infine, va menzionato che anche le equazioni cubiche e i polinomi superiori possono essere fattorizzati, sebbene questo processo diventi rapidamente impraticabilmente complicato.
Consigli
- a-b può essere scomposto, ma a+b no.
- Impara come fattorizzare le costanti: questo può aiutare.
- Fai attenzione alle frazioni durante la fattorizzazione ed elaborale correttamente e con attenzione.
- Se hai un trinomio della forma x+bx+ (b/2), allora la forma fattorizzata è (x+(b/2)) (puoi incontrarlo con una formula quadrata).
- Ricorda che a x 0 = 0.
Necessità
- Carta
- Matita
- Libro di matematica (se necessario)
Articoli sull'argomento "Equazioni fattorizzanti"
Condividi sui social network:
Popolare