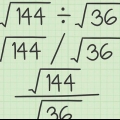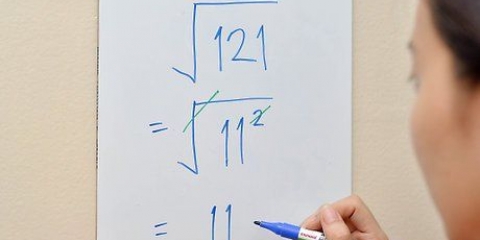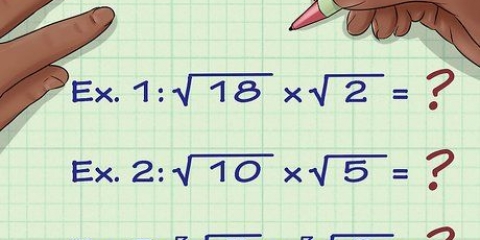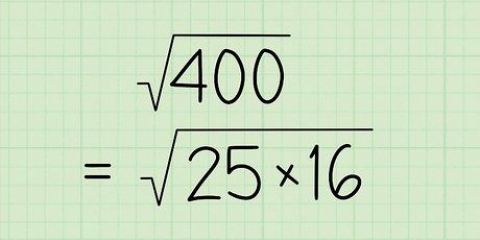Un altro esempio: vogliamo trovare la radice quadrata di 25 (√(25)). Ciò significa che dobbiamo trovare il numero che moltiplicato per se stesso ha 25 come prodotto. Poiché 5 = 5 × 5 = 25, possiamo dire che √(25) = 5. Puoi anche pensare a questo come "annullare" un quadrato (o numero di potenza). Ad esempio, se vogliamo trovare la radice quadrata di 64 (√64), consideriamo 64 come 8. prima. Poiché un radicale in linea di principio `elimina` un quadrato, possiamo dire che √(64) = √(8) = 8. 
D`altra parte, vengono chiamati i numeri che non danno numeri interi dopo la radice quadrata, quadrato imperfetto. Quando prendi la radice quadrata di uno di questi numeri, di solito ottieni un decimale o una frazione. A volte i decimali coinvolti possono diventare davvero disordinati. Ad esempio, √(13) = 3.605551275464… 
1 = 1 × 1 = 1 2 = 2 × 2 = 4 3 = 3 × 3 = 9 4 = 4 × 4 = 16 5 = 5 × 5 = 25 6 = 6 × 6 = 36 7 = 7 × 7 = 49 8 = 8 × 8 = 64 9 = 9 × 9 = 81 10 = 10 × 10 = 100 11 = 11 × 11 = 121 12 = 12 × 12 = 144 
Supponiamo di voler calcolare la radice quadrata di 900. A prima vista sembra molto difficile! Tuttavia, non è difficile se calcoliamo 900. I "fattori" sono quei numeri che possono moltiplicarsi insieme per formare un altro numero. Ad esempio, poiché 6 è il prodotto di 1 × 6 e 2 × 3, i fattori di 6 sono i numeri 1, 2, 3 e 6. Invece di calcolare con il numero 900, che è un po` scomodo, lo scriviamo come 9 × 100. Ora, poiché 9 è un quadrato perfetto e separato da 100, possiamo prendere la sua radice quadrata. √(9 × 100) = √(9) × √(100) = 3 × √(100). In altre parole, √(900) = 3√(100). Possiamo semplificare ulteriormente questi due passaggi dividendo 100 nei fattori 25 e 4. √(100) = √(25 × 4) = √(25) × √(4) = 5 × 2 = 10. Quindi possiamo dire che √(900) = 3(10) = 30. 
Nota: sebbene i numeri immaginari non possano essere rappresentati con numeri regolari, possono comunque essere trattati come numeri regolari in molti modi. Ad esempio, le radici dei numeri negativi possono essere quadrate per dare quei numeri negativi proprio come qualsiasi altra radice quadrata. Ad esempio: io = -1. 

Nel nostro esempio dividiamo 6,45 in coppie come questa: 6-,45-00. Nota che c`è un numero "rimanente" sulla sinistra &mdash questo è il punto. 
Nel nostro esempio, il primo gruppo in 6-,45-00 è il 6. Il numero più grande minore o uguale a 6 è 2 — 2 = 4. Scrivi un `2` sopra il 6 sotto il radicale. 
Nel nostro esempio, inizieremo con il doppio di 2, la prima cifra della nostra risposta. 2 × 2 = 4. Quindi sottraiamo 4 da 6 (il nostro primo `gruppo`) e otteniamo 2 come risposta. Quindi spostiamo il gruppo successivo (45) di una riga per ottenere 245. Infine, ne scriveremo altri 4 a sinistra, lasciando un po` di spazio da aggiungere alla fine, in questo modo: 4_. 
Nel nostro esempio, stiamo cercando il numero per riempire lo spazio vuoto in 4_ × _; ciò rende la risposta il più ampia possibile, ma comunque inferiore o uguale a 245. In questo caso la risposta è 5. 45 × 5 = 225, mentre 46 × 6 = 276. 
Continuiamo con il nostro esempio e continuiamo con 225 - 245 = 20. Quindi abbassiamo la coppia di cifre successiva, 00, per fare 2000. Se raddoppiamo il numero sopra il radicale, otteniamo 25 × 2 = 50. Risolviamo l`incognita in 50_ × _ =/< 2000, poi arriviamo 3 come risposta. A questo punto abbiamo `253` sopra il radicale — ripetendolo ancora, 9 è la cifra successiva. 
Nel nostro esempio, il numero sotto il segno radicale è 6,45, quindi spostiamo semplicemente il punto decimale in alto e lo posizioniamo tra 2 e 5 della nostra risposta, che ci dà 2.539 rendimenti. 

Nel nostro problema di esempio, una stima ragionevole per la radice quadrata di 40 è forse 6.4, perché da quanto sopra sappiamo che la risposta è probabilmente leggermente più vicina a 6 che a 7. 
Moltiplica 6,4 per se stesso, quindi 6,4 × 6,4 = 40.96, che è leggermente più grande del numero originale. Quindi moltiplichiamo il numero per un decimo inferiore alla nostra stima sopra (perché la nostra risposta era troppo alta) e otteniamo 6,3 × 6,3 = 39.69. Questo è leggermente inferiore al nostro numero originale. Ciò significa che la radice quadrata di 40 è da qualche parte tra 6.3 e 6.4 bugie. Inoltre, poiché 39,69 è più vicino a 40 che a 40,96, sai che la radice quadrata è più vicina a 6,3 che a 6,4. 
Nel nostro esempio, scegliamo 6,33 per la nostra ipotesi in due cifre decimali. Piazza 6.33 e ottieni 6.33 × 6.33 = 40.0689. Poiché questo è leggermente al di sopra del nostro numero originale, proveremo un numero leggermente inferiore, ad esempio 6,32. 6,32 × 6,32 = 39,9424. Questo è leggermente inferiore al nostro numero originale, quindi sappiamo che l`esatta radice quadrata tra 6.33 e 6.32 bugie. Se volessimo andare oltre, possiamo continuare a utilizzare lo stesso approccio per ottenere una risposta sempre più precisa.
Risolvi le radici quadrate
Contenuto
Mentre la vista intimidatoria di un simbolo di radice quadrata può far rabbrividire le persone con ansia per la matematica, i problemi di radice quadrata non sono così difficili da risolvere come sembrano a prima vista. Semplici problemi di radice quadrata possono spesso essere risolti con la stessa facilità dei semplici problemi di moltiplicazione e divisione. Problemi di radice quadrata più complessi, invece, potrebbero richiedere un po` più di lavoro, ma con il giusto approccio anche questi problemi possono essere risolti facilmente. Inizia oggi stesso a esercitarti sui problemi con la radice quadrata per apprendere questa abilità matematica che potrebbe essere nuova per te!
Passi
Parte 1 di 3: Capire poteri e radici

1. Quadra un numero moltiplicandolo per se stesso. Per capire le radici, è meglio iniziare con i quadrati. I quadrati sono facili: quadrare un numero equivale a moltiplicarlo per se stesso. Ad esempio: 3 al quadrato equivale a 3 × 3 = 9 e 9 al quadrato equivale a 9 × 9 = 81. I quadrati sono indicati da un piccolo "2" sopra ea destra del numero al quadrato, in questo modo: 3, 9, 100, ecc.
- Prova tu stesso a quadrare alcuni numeri per testare questo concetto. Ricorda che quadrare un numero non è altro che moltiplicare quel numero per se stesso. Puoi farlo anche con numeri negativi. In tutti i casi, la risposta sarà sempre positiva. Ad esempio: -8 = -8 × -8 = 64.

2. Per trovare la radice di un numero, trova l`inverso di un quadrato. Il simbolo della radice quadrata (√, noto anche come `segno radicale`) è sostanzialmente l``opposto` del simbolo quadrato (). Se vedi un segno radicale, puoi chiederti: `Quale numero posso moltiplicare per se stesso in modo da ottenere il numero sotto il segno radicale??` Ad esempio: se vedi la radice quadrata √(9), allora stai cercando il numero che moltiplicato per se stesso ha nove come prodotto. In questo caso è così tre, perché 3 = 9.

3. Conosci la differenza tra quadrati perfetti e imperfetti. Finora, le risposte ai problemi della radice quadrata erano belle, numeri rotondi. Non è sempre così, infatti ci sono risposte alle radici quadrate che sono numeri decimali molto lunghi e scomodi. Vengono chiamati i numeri radice che sono numeri interi (in altre parole, numeri che non sono frazioni o decimali) piazze. Tutti gli esempi precedenti (9, 25 e 64) sono quadrati (chiamati anche quadrati perfetti), perché prendendo le radici quadrate, otteniamo come risultato numeri interi (3, 5 e 8).

4. Memorizza i primi 10-12 quadrati. Come probabilmente avrai notato, le radici quadrate o i quadrati sono spesso molto facili! Poiché questi problemi di matematica sono così semplici, vale la pena dedicare del tempo a imparare le radici dei primi 12 o più quadrati. Incontrerai molto questi numeri, quindi puoi risparmiare molto tempo a lungo termine imparandoli presto. I primi 12 quadrati sono:

5. Semplifica le radici rimuovendo i quadrati ove possibile. Trovare le radici dei quadrati imperfetti a volte può essere complicato, specialmente se non usi una calcolatrice (i paragrafi seguenti ti danno dei trucchi per rendere più facile questo processo). Tuttavia, è spesso possibile semplificare i numeri sotto il segno radicale, per facilitare il lavoro con essi. Per fare ciò, devi solo scomporre il numero sotto il radicale, quindi prendere la radice quadrata dei fattori quadrati e scrivere la risposta al di fuori del radicale. È più facile di quanto sembri: continua a leggere per saperne di più!

6. Usa numeri immaginari per le radici dei numeri negativi. Quale quadrato è -16? Non è 4 o -4 — quadrando entrambi dà 16 (positivo). Non sai? In effetti, non c`è modo di scrivere la radice quadrata di -16 o qualsiasi numero negativo con numeri regolari. In questi casi è necessario utilizzare numeri immaginari (solitamente sotto forma di lettere o simboli) per sostituire la radice quadrata del numero negativo. Ad esempio, la variabile `i` viene solitamente utilizzata per la radice quadrata di -1. Come regola generale, la radice quadrata di un numero negativo sarà sempre un numero immaginario (o ne conterrà uno).
Parte 2 di 3: Utilizzo di algoritmi di divisione lunga

1. Ordina il tuo problema con la radice quadrata come la divisione lunga. Anche se può richiedere un po` di tempo, è possibile calcolare le radici di quadrati imperfetti difficili senza una calcolatrice. Per fare ciò, utilizziamo un metodo risolutivo (o algoritmo) che è simile a — ma non esattamente uguale a — una lunga divisione.
- Per prima cosa scrivi la radice quadrata allo stesso modo della divisione lunga. Ad esempio, supponiamo di voler calcolare la radice quadrata di 6,45, che non è certamente un quadrato perfetto conveniente. Per prima cosa scriviamo un normale simbolo radicale (√), quindi scriviamo il numero sotto di esso. Successivamente, tracciamo una linea sopra il numero in modo che sia in una piccola "scatola", proprio come una divisione lunga. Quando abbiamo finito, abbiamo notato un "√" allungato con 6,45 sotto di esso.
- Scriviamo i numeri sopra il problema, quindi lascia un po` di spazio.

2. Raggruppa i numeri a coppie. Per risolvere il tuo problema, raggruppa le cifre del numero sotto il segno del radicale a coppie, partendo dal punto decimale. Puoi aggiungere piccoli punti salienti (come punti, barre, virgole, ecc.) tra le tue coppie per distinguerle.

3. Trova il numero più grande il cui quadrato è minore o uguale al primo `gruppo`. Inizia con il primo numero o coppia a sinistra. Scegli il numero più grande con un quadrato minore o uguale al `gruppo`. Ad esempio, se il gruppo è 37, sceglieresti il 6, perché 6 = 36 (meno di 37), ma 7 = 49 (maggiore di 37). Scrivi questo numero sopra il primo gruppo. Questa è la prima cifra della tua risposta.

4. Raddoppia il numero che hai appena annotato, scrivilo sotto il primo gruppo e sottrailo. Prendi la prima cifra della tua risposta (il numero che hai appena trovato) e raddoppiala. Scrivi questo sotto il tuo primo gruppo e sottrailo per trovare la differenza. Posiziona la coppia di numeri successiva accanto alla risposta di seguito. Infine, scrivi l`ultima cifra del doppio della prima cifra della tua risposta a sinistra, lasciando uno spazio accanto ad essa.

5. Riempi lo spazio vuoto. Successivamente, l`intenzione è aggiungere una cifra a destra del numero che hai scritto a sinistra. Scegli un numero che moltiplica per il tuo nuovo numero produce il prodotto più grande possibile, ma è inferiore o uguale al numero "estratto". Ad esempio, se il tuo numero "ridotto" è 1700 e il numero a sinistra è 40_, dovresti riempire lo spazio vuoto con "404" perché 404 × 4 = 1616 (meno di 1700), mentre 405 × 5 = 2025. Il numero che trovi in questo passaggio è la seconda cifra della tua risposta, quindi puoi aggiungerla sopra il radicale.

6. Continua a usare i tuoi numeri "vuoti" per la tua risposta. Continua con questa divisione lunga modificata finché non ottieni zeri quando sottrai il numero "disegna verso il basso" o hai raggiunto la precisione desiderata. Quando hai finito, i numeri che hai usato per riempire gli spazi vuoti ad ogni passaggio (più il primo numero che hai usato) sono le cifre della tua risposta.

7. Sposta in alto il punto decimale del tuo "divisore" originale. Per arrotondare la tua risposta, devi mettere la virgola (il punto decimale) al posto giusto. Fortunatamente, questo è facile: tutto ciò che devi fare è allinearlo con il punto decimale nel tuo numero originale. Se il numero sotto il radicale è 49,8, sposta il punto decimale in alto tra i due numeri sopra 9 e 8.
Parte 3 di 3: Stimare rapidamente i quadrati imperfetti

1. Trova i quadrati imperfetti stimando. Una volta che hai memorizzato i tuoi quadrati, trovare le radici dei quadrati imperfetti diventa molto più facile. Poiché conosci già una dozzina di quadrati, qualsiasi numero che rientri tra due di questi quadrati perfetti può essere trovato stimando tra questi valori. Per iniziare, trova i due quadrati in cui si trova il tuo numero. Quindi determina quale di questi due quadrati è più vicino al numero.
- Ad esempio, supponiamo di dover trovare la radice quadrata di 40. Dato che abbiamo memorizzato i nostri quadrati, possiamo dire che 40 cade tra 6 e 7, oppure 36 e 49. Poiché 40 è maggiore di 6, la sua radice quadrata sarà maggiore di 6 e poiché è minore di 7, la sua radice quadrata sarà minore di 7. Il numero 40 è un po` più vicino a 36 che a 49, quindi la risposta sarà probabilmente un po` più vicina a 6. Nei prossimi passi renderemo la nostra risposta più accurata.

2. Stimare la radice quadrata con una cifra decimale. Una volta che hai scelto due caselle tra le quali si trova il tuo numero, è solo una questione di stima finché non trovi una risposta di cui sei soddisfatto. Più vai avanti, più precisa sarà la tua risposta. Per iniziare, scegli un dieci per la tua risposta: non deve essere corretto, ma risparmierai tempo se usi il buon senso scegliendo un numero vicino alla risposta corretta.

3. Moltiplica la stima per se stessa. Quindi quadra la stima. A meno che tu non sia fortunato, probabilmente non otterrai il tuo numero originale: finirai leggermente più alto o più basso. Se la tua risposta è troppo alta, riprova con una stima leggermente inferiore (e viceversa se è troppo bassa).

4. Continuare a stimare se necessario. Se sei soddisfatto delle tue risposte, potresti voler usare solo una delle tue prime ipotesi. Tuttavia, se vuoi una risposta più accurata, tutto ciò che devi fare è scegliere una stima per il tuo "centesimo" che metta questa stima tra le prime due. Se continui con questo schema, puoi ottenere una risposta in tre, quattro o più cifre decimali: dipende solo da quanto lontano vuoi andare.
Consigli
- Per soluzioni rapide, usa una calcolatrice. La maggior parte dei moderni calcolatori può calcolare direttamente le radici quadrate. Solitamente basta inserire il proprio numero e poi premere il pulsante con il radicale della seconda potenza (la radice quadrata). Ad esempio, per trovare la radice quadrata di 841, premere i seguenti tasti: 8, 4, 1, (√) e ottenere il risultato corretto 29 su come risposta.
Articoli sull'argomento "Risolvi le radici quadrate"
Condividi sui social network:
Popolare