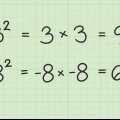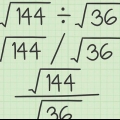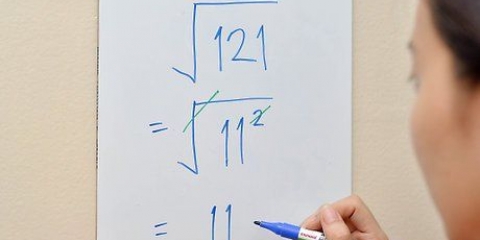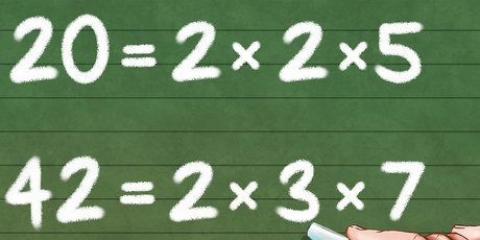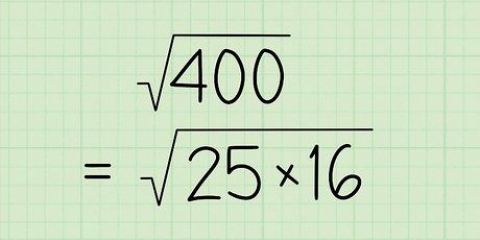Semplificare le Radici Quadrate

Contenuto

Passi
Consigli
Avvertenze

Semplificare una radice quadrata non è così difficile come sembra. Per semplificare una radice quadrata devi solo scomporre il numero della radice quadrata e provare a prendere la radice quadrata di uno o entrambi i fattori. Una volta che conosci alcuni numeri quadrati comuni e sai come dividere un numero in fattori, sei sulla buona strada per semplificare una radice quadrata. Ecco come puoi impararlo rapidamente.

Passi

Metodo 1 di 4: semplificare la radice quadrata di un numero

Immagine titolata Simplify a Square Root Step 1

1. Impara alcuni numeri quadrati e le loro radici. La quadratura, moltiplicando un numero per se stesso, fa un numero al quadrato (perfettamente quadrato). Ad esempio: 25 è un numero al quadrato perché 5 x 5, o 5, è uguale a 25. Conoscere almeno i primi 10 dieci numeri al quadrato può aiutare a riconoscere e semplificare le radici quadrate. Ecco i primi dieci numeri al quadrato:

1 = 1
2 = 4
3 = 9
4 = 16
5 = 25
6 = 36
7 = 49
8 = 64
9 = 81
10 = 100

2. Trova la radice quadrata di un numero quadrato. Se vedi un numero quadrato sotto un radicale, devi solo rimuovere il radicale (√ ) e scrivere la radice quadrata del numero quadrato. Se l`avevi già imparato a memoria, allora hai finito. Se il numero è troppo grande e non sei sicuro che sia un numero quadrato, prova a trovare la radice quadrata con la calcolatrice per verificare se produce un bel numero tondo. Ad esempio: a √25 sai che la risposta è uguale a 5 perché 25 è un numero al quadrato.

Metodo 2 di 4: semplificazione di una radice quadrata mediante factoring

Immagine titolata Simplify a Square Root Step 4

1. Se il numero è pari, dividilo per 2. Trovare i fattori di un numero implica trovare tutti i numeri che moltiplicati insieme producono quel numero, rendendo più facile determinarne la radice quadrata. Se è un numero pari, la prima cosa che puoi fare è dividere il numero per 2. In questo esempio puoi dividere √98 in √(2x49), perché 98 : 2 =49. Se il numero non è divisibile per 2, prova 3, 4, 5 e così via, finché non trovi la combinazione giusta.

Immagine titolata Simplify a Square Root Step 5

2. Dividi nuovamente questi fattori in fattori per trovare ulteriori numeri quadrati. Vedi se riesci a continuare a dividere il numero in fattori. 2 è primo e ha solo se stesso e 1 come divisore. Ma 49, l`altro fattore, può ancora essere diviso in 7 x 7, perché è un numero quadrato. Quindi puoi riscrivere la radice √(2x49) come √(2x7x7), o √[2(7)], il che significa che abbiamo già trovato il numero quadrato che stavamo cercando.

Immagine titolata Simplify a Square Root Step 6

3. Semplifica la radice quadrata. Poiché √98= √[2(7)], è possibile porre un 7 al di fuori del radicale e semplificare la risposta a 7√2. Quindi √49 o anche (7 x 7), poi diventa 7 non appena lo metti al di fuori del radicale. Se rimetti di nuovo il 7, diventa di nuovo un numero quadrato e quindi 49. Quindi, √98 = 7√2.

Metodo 3 di 4: Altri metodi per semplificare una radice quadrata

1. Se non riesci immediatamente a trovare un numero quadrato, dividi ulteriormente il numero. Ad esempio, se il problema è √48, continui a dividere finché non puoi andare oltre 2x2, in modo che 4 diventi un coefficiente del radicale e 3 rimanga all`interno del radicale. Ecco come funziona:

√48 = √(2 x 24)
√(2 x 24) = √(2 x 12 x 2)
√(2 x 12 x 2) = √(2 x 6 x 2 x 2)
√(2 x 6 x 2 x 2) = √(2 x 3 x 2 x 2 x 2)
√(2 x 3 x 2 x 2 x 2) = √(2 x 3)
√(2 x 3)= 4√3
√48 = 4√3

2. Ricorda che non puoi semplificare un numero primo. Questo perché i fattori qui sono 1 e il numero primo stesso. Ad esempio: √17 non può essere semplificato perché 17 è primo.

3. Dividere in fattori di più di un numero al quadrato. Se i fattori del numero contengono più di un numero quadrato, portali tutti al di fuori del radicale. Se hai trovato più quadrati durante la semplificazione, portali tutti al di fuori del radicale e moltiplicali. Ad esempio: supponiamo di voler semplificare il numero √32, quindi dividerlo nei fattori 4 x 4 x 2, notando che il numero quadrato 4 ricorre due volte. Fai questo 16√2 che alla fine produrrà 4√2.

4. Non confondere il coefficiente con una radice di potenza più alta. 3√125, per esempio, è uguale a 3 x √125, ma √125 è la radice cubica di 125. (perché 5 x 5 x 5 = 125, √125 = 5.)

Metodo 4 di 4: Conoscere la terminologia

1. Ricorda che il radicale (√) è il simbolo della radice quadrata. Ad esempio, nel problema √25, "√" il segno radicale.

2. Ricorda che il radicale è il numero sotto il radicale. Trova la radice quadrata di questo numero. Ad esempio: a √25 è "25" il numero di radice.

3. Ricorda che il coefficiente è il numero al di fuori del radicale. Questo numero moltiplica la radice quadrata; Questo può essere trovato a sinistra del segno radicale, il simbolo √. Ad esempio: a 7√2, "7" il coefficiente.

4. Ricorda che un fattore è un numero che va completamente in un altro numero. Ad esempio: 2 è un fattore 8 perché 8 ÷ 4 = 2, ma 3 non è un fattore 8 perché 8÷3 non risponde a un numero intero. Ad esempio: 5 è un fattore di 25 perché 5 x 5 = 25.

5. Comprendere il significato di semplificare una radice quadrata. Semplificare una radice quadrata implica semplicemente dividere un quadrato di una radice quadrata in fattori, quindi spostarlo a sinistra del radicale, lasciando l`altro fattore all`interno del radicale. Se il numero è un numero quadrato, puoi rimuovere il segno radicale non appena hai scritto la sua radice quadrata. Ad esempio: √98 può essere semplificato a 7√2.

Consigli

Un modo per trovare i quadrati per dividere i numeri al quadrato è cercare i quadrati nell`elenco che iniziano con il numero più piccolo dopo il numero al quadrato. Ad esempio: se stai cercando il numero quadrato di 27, inizia da 25 e fermati a 9, perché hai trovato il massimo divisore che è un numero quadrato.

Avvertenze

Non utilizzare calcolatrici tranne nel passaggio in cui stai cercando di capire quante volte il quadrato va nella radice quadrata.
Semplificare non è come inserire valori in un`equazione.Da nessuna parte nell`intero processo può apparire un numero decimale da nessuna parte!