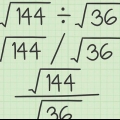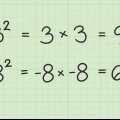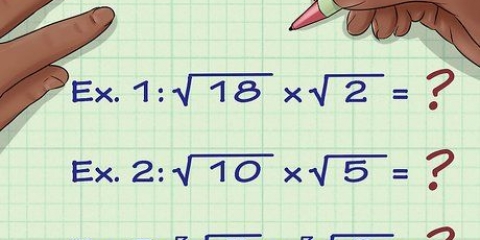Moltiplicare le Radici Quadrate: 8 Passaggi (con Immagini)

Contenuto

Passi
- Metodo 1 di 2: Moltiplicare le radici quadrate senza coefficienti
- Metodo 2 di 2: Moltiplicare le radici quadrate con i coefficienti
Consigli
Necessità

Proprio come moltiplicando interi, puoi anche moltiplicare le radici quadrate (un`equazione radice quadrata) insieme. A volte le radici quadrate hanno coefficienti (un intero prima del radicale), ma questo aggiunge solo un passaggio alla moltiplicazione e non cambia il processo. La parte più complicata della moltiplicazione della radice quadrata è semplificare l`espressione per ottenere la risposta finale, ma anche questo passaggio è facile se conosci i tuoi quadrati perfetti.

Passi

Metodo 1 di 2: Moltiplicare le radici quadrate senza coefficienti

Immagine titolata Multiply Square Roots Step 1

1. Moltiplica le radici insieme. Un radicando (inglese) è un numero sotto il radicale. Moltiplica le radici allo stesso modo degli interi. Assicurati che il prodotto rimanga al di sotto del segno radicale.

Ad esempio, se calcoli $\sqrt{15} \times \sqrt{5}$ ${sqrt{15}}volte {sqrt{5}}$ , allora ottieni $15 \times 5 = 75$ $15volte 5=75$ . così, $\sqrt{15} \times \sqrt{5} = \sqrt{75}$ ${sqrt{15}}times {sqrt{5}}={sqrt{75}}$ .

Immagine titolata Multiply Square Roots Step 2

2. Ricava qualsiasi quadrato perfetto dalla radice quadrata. Puoi farlo controllando se un quadrato perfetto è un fattore del numero sotto il radicale. Se non riesci a ricavare un quadrato perfetto, la tua risposta è già stata semplificata e non devi fare nient`altro.

Un quadrato perfetto è il risultato della moltiplicazione di un numero (intero positivo o negativo) per se stesso. Ad esempio: 25 è un quadrato perfetto perché

5 \times 5 = 25

$5volte 5=25$ .

Ad esempio,

\sqrt{75}

${sqrt{75}}$ può essere scomposto nel quadrato perfetto 25:

\sqrt{75}

${sqrt{75}}$
=

\sqrt{25 \times 3}

${sqrt{25volte 3}}$

Immagine titolata Multiply Square Roots Step 3

3. Metti la radice quadrata prima del radicale. Lascia l`altro fattore sotto il radicale. Ora hai l`espressione semplificata.

Ad esempio,

\sqrt{75}

${sqrt{75}}$ può essere sciolto

\sqrt{25 \times 3}

${sqrt{25volte 3}}$ , per la radice quadrata di 25 (che è 5):

\sqrt{75}

${sqrt{75}}$
=

\sqrt{25 \times 3}

${sqrt{25volte 3}}$
=

5 \sqrt{3}

$5{sqrt{3}}$

Immagine titolata Multiply Square Roots Step 4

4. Calcola il quadrato di una radice quadrata. In alcuni casi è necessario moltiplicare una radice quadrata per se stessa. La quadratura di un numero e la radice quadrata di un numero sono operazioni opposte; quindi si annullano a vicenda. Il risultato del quadrato di una radice quadrata è semplicemente il numero sotto il radicale.

Ad esempio,

\sqrt{25} \times \sqrt{25} = 25

${sqrt{25}}times {sqrt{25}}=25$ . Ottieni questo risultato perché

\sqrt{25} \times \sqrt{25} = 5 \times 5 = 25

${sqrt{25}}volte {sqrt{25}}=5volte 5=25$ .

Metodo 2 di 2: Moltiplicare le radici quadrate con i coefficienti

Immagine titolata Multiply Square Roots Step 5

1. Moltiplica i coefficienti. Un coefficiente è un numero per il radicale. Ignora semplicemente il radicale e il numero sotto di esso e moltiplica i due numeri interi insieme. Metti il loro prodotto prima del primo radicale.

Fare attenzione ai segni più e meno quando si moltiplicano i coefficienti. Ricorda che un numero negativo moltiplicato per un numero positivo produce un risultato negativo e un numero negativo moltiplicato per un numero negativo produce un risultato positivo.
Ad esempio, durante il calcolo $3 \sqrt{2} \times 2 \sqrt{6}$ $3{sqrt{2}}volte 2{sqrt{6}}$ , calcola prima $3 \times 2 = 6$ $3volte 2=6$ . Ora il compito è il seguente: $6 \sqrt{2} \times \sqrt{6}$ $6{sqrt{2}}volte {sqrt{6}}$ .

Immagine titolata Multiply Square Roots Step 6

2. Moltiplica i numeri sotto i radicali. Per fare ciò, moltiplica i numeri come se fossero interi. Assicurati che il prodotto rimanga sotto il segno radicale.

Ad esempio, per una dichiarazione come

6 \sqrt{2} \times \sqrt{6}

$6{sqrt{2}}volte {sqrt{6}}$ , calcola il prodotto dei numeri sotto i radicali usando

2 \times 6 = 12

$2volte 6=12$ , così che

\sqrt{2} \times \sqrt{6} = \sqrt{12}

${sqrt{2}}times {sqrt{6}}={sqrt{12}}$ . L`attività ora si presenta così:

6 \sqrt{12}

$6{sqrt{12}}$ .

Immagine titolata Multiply Square Roots Step 7

3. Se possibile, scomponi i quadrati sotto il segno radicale. Devi farlo per semplificare la tua risposta. Se non riesci a risolvere un quadrato, la tua risposta è già stata semplificata e puoi saltare questo passaggio.

Un quadrato è il risultato della moltiplicazione di un intero (positivo o negativo) per se stesso. Ad esempio: 4 è un quadrato, perché

2 \times 2 = 4

$2volte 2=4$ .

Ad esempio:

\sqrt{12}

${sqrt{12}}$ può essere scomposto in modo che il quadrato di 4 sia posto prima del radicale:

\sqrt{12}

${sqrt{12}}$
=

\sqrt{4 \times 3}

${sqrt{4volte 3}}$

Immagine titolata Multiply Square Roots Step 8

4. Moltiplica la radice del quadrato per il coefficiente. Lascia l`altro fattore sotto il radicale. Questo produce un`espressione semplificata.

Ad esempio,

6 \sqrt{12}

$6{sqrt{12}}$ può essere sciolto

6 \sqrt{4 \times 3}

$6{sqrt{4volte 3}}$ , dopo di che puoi prendere la radice quadrata di 4 (che è 2) dopo di che lo moltiplichi per 6:

6 \sqrt{12}

$6{sqrt{12}}$
=

6 \sqrt{4 \times 3}

$6{sqrt{4volte 3}}$
=

6 \times 2 \sqrt{3}

$6volte 2{sqrt{3}}$
=

12 \sqrt{3}

$12{sqrt{3}}$

Consigli

Conosci i tuoi quadrati, perché questo rende questo processo molto più semplice!
Segui le normali regole per il segno di un numero per determinare se il nuovo coefficiente sarà positivo o negativo. Un coefficiente positivo moltiplicato per un coefficiente negativo dà un numero negativo. Due coefficienti positivi moltiplicati insieme o due coefficienti negativi moltiplicati insieme danno un numero positivo.
Tutti i termini sotto il radicale sono sempre positivi, quindi non devi preoccuparti del segno quando moltiplichi i numeri sotto un radicale.