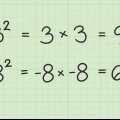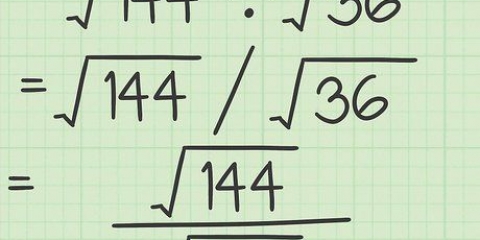In questo esempio, il primo insieme di tre numeri moltiplicati insieme è uguale a 10. Determina il cubo più grande che è inferiore a 10. Questo è 8 e la sua radice cubica è 2. Scrivi il numero 2 sopra il segno del radicale, sopra il numero 10. Annota il valore di  , uguale a 8, al di sotto del numero 10; traccia una linea e sottrai i numeri come nella divisione lunga. Il risultato è 2.
, uguale a 8, al di sotto del numero 10; traccia una linea e sottrai i numeri come nella divisione lunga. Il risultato è 2. Dopo questa somma meno hai la prima cifra della tua risposta. Dovrai verificare se questo numero è sufficientemente esatto. Nella maggior parte dei casi non sarà così. Puoi verificarlo alzando il numero al cubo e vedendo se è abbastanza vicino al risultato desiderato. In questo caso  è uguale a 8, e non è molto vicino a 10, quindi devi andare avanti.
è uguale a 8, e non è molto vicino a 10, quindi devi andare avanti. 
A sinistra della linea verticale, annota la soluzione del divisore successivo, come somma di tre numeri separati. Indica gli spazi vuoti per questi numeri sottolineando tre spazi vuoti con il segno più sotto di essi. 


Ora calcola 3 volte 10 volte ciascuno dei due numeri che esistono nella tua soluzione sopra il radicale. Per questo semplice problema, ciò significa 3*10*2*1, che è uguale a 60. Aggiungi questo ai 1200 che già avevi e otterrai 1260. Infine, aggiungi il quadrato dell`ultima cifra. In questo esempio, è 1; e 1^2 è ancora 1. Quindi il divisore totale è 1200+60+1, o 1261. Nota questo a sinistra della linea verticale. 

Puoi controllare la precisione di questo risultato usando il cubo: 2.1*2.1*2.1. Il risultato è 9.261. Se pensi che il risultato sia abbastanza esatto, puoi fermarti. Se vuoi una risposta più precisa, devi passare attraverso un altro round. 
Prendi il prossimo gruppo di tre numeri verso il basso. In questo caso si tratta di tre zeri, che vengono dopo il resto 739 e quindi 739.000 forme. Inizia il divisore a 300 volte il quadrato del numero attualmente sopra il radicale. Questo è  , e quindi 132.300.
, e quindi 132.300. Seleziona la cifra successiva della tua soluzione in modo da poterla moltiplicare per 132.300 e meno dal 739.000 del tuo resto. Una buona scelta sarebbe 5, perché 5*132.300=661.500. Scrivi il numero 5 nello spazio successivo sopra la linea dei radicali. Trova 3 volte il numero precedente sopra la linea del radicale, 21, per l`ultima cifra che hai appena annotato, 5, per 10. Questo da  .
. Infine, quadra l`ultima cifra. Questo è 
Somma i termini del tuo divisore e ottieni 132.300+3150+25=135.475. 
Moltiplica il divisore per l`ultima cifra della tua soluzione. 135.475*5=677.375. sottrarre. 739.000-677.375=61.625. Considera se la soluzione 2.15 è sufficientemente esatta. Calcola il suo cubo e ottieni  .
. 


Nel problema di esempio, 600 (il tuo numero target) cade a metà strada tra i numeri limite 512 e 729. Quindi scegli il tuo 5 come prossimo numero. 
In questo esempio, moltiplichi 

Ad esempio, in questo problema,  maggiore del target (600). Quindi riduci la stima a 8,4. Prendi il cubo di questo numero e confrontalo con il tuo obiettivo. lo vedrai
maggiore del target (600). Quindi riduci la stima a 8,4. Prendi il cubo di questo numero e confrontalo con il tuo obiettivo. lo vedrai  . Questo è ora inferiore al tuo obiettivo. Questo ti dice che la radice cubica di 600 deve essere almeno 8,4, ma inferiore a 8,5.
. Questo è ora inferiore al tuo obiettivo. Questo ti dice che la radice cubica di 600 deve essere almeno 8,4, ma inferiore a 8,5. 
In questo problema di esempio, il tuo ultimo ciclo di calcoli lo mostra  , mentre
, mentre  . Il target (600) è leggermente più vicino a 592 che a 614. Quindi stimi il numero successivo un po` meno della metà tra 0 e 9. Una buona scelta è 4, che ti darà una stima della radice cubica di 8,44.
. Il target (600) è leggermente più vicino a 592 che a 614. Quindi stimi il numero successivo un po` meno della metà tra 0 e 9. Una buona scelta è 4, che ti darà una stima della radice cubica di 8,44. 
Per questo problema di esempio, inizia osservandolo  . Questo è appena sopra il target, quindi rilasciane un po` e prova 8.43. Questo da
. Questo è appena sopra il target, quindi rilasciane un po` e prova 8.43. Questo da  come risultato. Quindi sai che la radice cubica di 600 è un po` più di 8,43 e un po` meno di 8,44.
come risultato. Quindi sai che la radice cubica di 600 è un po` più di 8,43 e un po` meno di 8,44. 
Per l`esempio della radice cubica di 600, assumendo due numeri decimali, 8,43 è inferiore a 1 dal numero target. Se continui a tre cifre dopo il punto decimale, lo vedrai  se il risultato è 0,1 in meno rispetto alla risposta effettiva.
se il risultato è 0,1 in meno rispetto alla risposta effettiva. 

Per saperne di più sul binomio di Newton e ottenere questo risultato, leggi di più sulla moltiplicazione dei binomi su wikiHow. Se vuoi una versione più approfondita e veloce, leggi di più sul Triangolo di Pascal. 

Il primo termine contiene un plurale di 1000. Per prima cosa scegli un numero che potrebbe essere elevato al cubo e rimanere ancora nell`intervallo della divisione lunga come prima cifra. Questo produce il termine 1000A^3 nel binomio. Il secondo termine del binomio di Newton ha un coefficiente di 300. (Questo è da  .) Ricorda che quando si calcola la radice cubica, la prima cifra in ogni passaggio è stata moltiplicata per 0300.
.) Ricorda che quando si calcola la radice cubica, la prima cifra in ogni passaggio è stata moltiplicata per 0300. La seconda cifra in ogni passaggio del calcolo della radice cubica deriva dal terzo termine del binomio di Newton. Nel binomio di Newton vedi il termine 30AB^2. L`ultima cifra di ogni passaggio è il termine B^3. 
Calcolo delle radici del cubo a mano
Contenuto
Usando una calcolatrice, calcolare la radice cubica di qualsiasi numero è solo premendo alcuni tasti. Ma forse non hai una calcolatrice o vuoi impressionare i tuoi amici con la tua capacità di calcolare una radice cubica a mano libera. C`è un metodo che a prima vista sembra un po` difficile, ma funziona molto facilmente con un po` di pratica. È utile avere alcune conoscenze pronte nel campo delle abilità aritmetiche e del calcolo dei numeri cubi.
Passi
Parte 1 di 3: Elaborazione di un compito di esempio

1. Prepara il compito. Risolvere la radice cubica di un numero sembrerà come risolvere la divisione lunga, con alcune differenze qua e là. Il primo passo è scrivere correttamente il problema.
- Annota il numero di cui vuoi trovare la radice cubica. Scrivi i numeri in gruppi di tre, dove la virgola è il punto di partenza. In questo esempio troverai la radice cubica di 10. Scrivilo come 10.000000. Gli zeri sono necessari per l`accuratezza della risposta.
- Disegna un radicale del cubo sopra il numero. Questo serve allo stesso scopo della linea di divisione lunga. L`unica differenza è la forma del simbolo.
- Metti una virgola sopra la riga, direttamente sopra la virgola decimale nel numero originale.

2. Conosci i cubi delle unità. Lo userai nei tuoi calcoli. Si tratta dei seguenti terzi poteri:











3. Trova la prima cifra della tua risposta. Seleziona un numero che, al cubo, dia il risultato più grande possibile inferiore al primo insieme di tre numeri.
 , uguale a 8, al di sotto del numero 10; traccia una linea e sottrai i numeri come nella divisione lunga. Il risultato è 2.
, uguale a 8, al di sotto del numero 10; traccia una linea e sottrai i numeri come nella divisione lunga. Il risultato è 2. è uguale a 8, e non è molto vicino a 10, quindi devi andare avanti.
è uguale a 8, e non è molto vicino a 10, quindi devi andare avanti.
4. Fai la scaletta per la cifra successiva. Scrivi il prossimo gruppo di tre numeri nel resto e traccia una breve linea verticale a sinistra del numero risultante. Questo sarà il numero che usiamo per determinare la cifra successiva nella tua soluzione di radice cubica. In questo esempio, questo sarà 2000, che viene creato dal resto 2 della precedente somma meno, con il gruppo di tre zeri che hai cancellato.

5. Trova l`inizio del prossimo divisore. Per la prima parte del divisore, scrivi trecento volte il quadrato di qualunque cosa sia al di sopra del radicale. In questo caso, sono 2; 2^2 è 4 e 4*300=1200. Quindi scrivi 1200 nel primo spazio vuoto. Il divisore per questo passaggio della soluzione sarà 1200, più qualcos`altro che calcolerai tra un minuto.

6. Trova il numero successivo nella tua radice cubica. Trova la cifra successiva della tua soluzione selezionando ciò che puoi moltiplicare per il divisore (1200 e qualcosa), quindi sottrai dal resto di 2000. Questo può essere solo 1, perché 2 per 1200 equivale a 2400, che è maggiore di 2000. Scrivi il numero 1 nello spazio successivo sopra il radicale.

7. Trova il resto del divisore. Il divisore in questo passaggio della soluzione è composto da tre parti. La prima parte sono i 1200 che hai già. Ora dovrai aggiungere due termini extra per completare il divisore.

8. Moltiplica e sottrai. Arrotonda questa parte della soluzione moltiplicando l`ultima cifra della tua soluzione - in questo caso il numero 1 - per il divisore che hai appena calcolato (1261). 1*1261 =1261. Scrivi questo sotto 2000 e sottrai 1261 da esso per ottenere 739.

9. Decidi che dovresti andare oltre per una risposta più accurata. Dopo aver completato la somma meno di ogni passaggio, devi verificare se la tua risposta è sufficientemente esatta. Per la radice cubica di 10: dopo la prima somma meno, la radice cubica era solo 2, e non è proprio esatto. Ora, dopo il secondo round, la soluzione è 2.1.

10. Determina il dealer per il prossimo round. In questo caso, per una maggiore pratica e una risposta più precisa, ripetere i passaggi per un altro round, come segue:
 , e quindi 132.300.
, e quindi 132.300. .
.

11. Moltiplica il divisore per il risultato. Dopo aver calcolato il divisore in questo round successivo e aver espanso la tua soluzione di un`altra cifra, procedi come segue:
 .
.
12. Scrivi la tua risposta finale. Il risultato sopra il radicale è la radice cubica, con una precisione di tre cifre significative. In questo esempio, la radice cubica di 10 è uguale a 2,15. Verificalo calcolando 2,15^3=9,94 che può essere arrotondato a 10. Se hai bisogno di una risposta più precisa, continua finché non sei soddisfatto.
Parte 2 di 3: Trovare la radice cubica attraverso la stima ripetuta

1. Usa i numeri cubi per impostare i limiti superiore e inferiore. Quando ti viene richiesta una radice cubica di un certo numero, inizia scegliendo un cubo che sia il più vicino possibile ad esso senza essere più grande del tuo numero target.
- Ad esempio, se vuoi trovare la radice cubica di 600, ricorda (o usa una tabella dei cubi) che
e
. Pertanto, la soluzione alla radice cubica di 600 sarà compresa tra 8 e 9. Usa i numeri 512 e 729 come limiti superiore e inferiore per la tua soluzione.

2. Indovina il prossimo numero. Conoscevi la prima cifra grazie alla tua conoscenza di determinati numeri cubi. Per la cifra successiva, stima un numero compreso tra 0 e 9 in base a dove il tuo numero di destinazione cade tra i due numeri limite.

3. Metti alla prova la tua ipotesi determinando il suo cubo. Prova a moltiplicare la stima con cui stai lavorando ora per vedere quanto sei vicino al numero target.


4. Modifica la tua stima ove necessario. Dopo aver rilanciato al cubo della tua ultima ipotesi, confronta il risultato con il tuo numero target. Se il risultato è maggiore dell`obiettivo, la stima dovrebbe essere inferiore. Se il risultato è inferiore all`obiettivo, devi regolarlo verso l`alto fino a raggiungere l`obiettivo.
 maggiore del target (600). Quindi riduci la stima a 8,4. Prendi il cubo di questo numero e confrontalo con il tuo obiettivo. lo vedrai
maggiore del target (600). Quindi riduci la stima a 8,4. Prendi il cubo di questo numero e confrontalo con il tuo obiettivo. lo vedrai  . Questo è ora inferiore al tuo obiettivo. Questo ti dice che la radice cubica di 600 deve essere almeno 8,4, ma inferiore a 8,5.
. Questo è ora inferiore al tuo obiettivo. Questo ti dice che la radice cubica di 600 deve essere almeno 8,4, ma inferiore a 8,5.
5. Stimare il numero successivo per una risposta più accurata. Continua questa procedura di stima dei numeri da 0 a 9, finché la tua risposta non è accurata come desideri. Per ogni giro di stima, inizia controllando la posizione del tuo ultimo calcolo tra i numeri limite.
 , mentre
, mentre  . Il target (600) è leggermente più vicino a 592 che a 614. Quindi stimi il numero successivo un po` meno della metà tra 0 e 9. Una buona scelta è 4, che ti darà una stima della radice cubica di 8,44.
. Il target (600) è leggermente più vicino a 592 che a 614. Quindi stimi il numero successivo un po` meno della metà tra 0 e 9. Una buona scelta è 4, che ti darà una stima della radice cubica di 8,44.
6. Continua a stimare e aggiustare Fallo tutte le volte che è necessario, aumenta la tua stima al cubo e guarda come si confronta con il numero target. Cerca i numeri che sono appena sotto o appena sopra il numero target.
 . Questo è appena sopra il target, quindi rilasciane un po` e prova 8.43. Questo da
. Questo è appena sopra il target, quindi rilasciane un po` e prova 8.43. Questo da  come risultato. Quindi sai che la radice cubica di 600 è un po` più di 8,43 e un po` meno di 8,44.
come risultato. Quindi sai che la radice cubica di 600 è un po` più di 8,43 e un po` meno di 8,44.
7. Continua fino a raggiungere la precisione desiderata. Continua a stimare, confrontare e ristimare, per tutto il tempo necessario, fino a quando la tua soluzione non sarà accurata come desideri. Nota che con ogni decimale, i tuoi numeri target si avvicinano sempre di più al numero effettivo.
 se il risultato è 0,1 in meno rispetto alla risposta effettiva.
se il risultato è 0,1 in meno rispetto alla risposta effettiva.Parte 3 di 3: Capire come funziona questo calcolo

1. Ripassa di nuovo il binomio di Newton. Per capire perché questo algoritmo funziona per determinare le radici del cubo, devi prima ripensare a come appare il cubo come binomio. Probabilmente l`hai imparato al liceo di matematica (e come la maggior parte delle persone, probabilmente te ne sei dimenticato abbastanza rapidamente). Seleziona due variabili  e
e  per rappresentare le unità. Quindi calcoli il binomio di
per rappresentare le unità. Quindi calcoli il binomio di  per le decine.
per le decine.
 e
e  per rappresentare le unità. Quindi calcoli il binomio di
per rappresentare le unità. Quindi calcoli il binomio di  per le decine.
per le decine. - Usa il termine
per crearne una dozzina. Qualunque sia il grado per cui scegli
,
formeranno una dozzina. Ad esempio, se
è 2 e
è 6, quindi diventa
pari a 26.

2. Scrivi il binomio in un cubo. Ora lavoriamo a ritroso, determinando prima il cubo e poi vedendo perché la soluzione delle radici del cubo funziona. Abbiamo bisogno dei valori di  trovare. Lo fai allenandoti
trovare. Lo fai allenandoti  . Questo è un calcolo troppo lungo per essere mostrato qui, ma il risultato finale lo è
. Questo è un calcolo troppo lungo per essere mostrato qui, ma il risultato finale lo è  .
.
 trovare. Lo fai allenandoti
trovare. Lo fai allenandoti  . Questo è un calcolo troppo lungo per essere mostrato qui, ma il risultato finale lo è
. Questo è un calcolo troppo lungo per essere mostrato qui, ma il risultato finale lo è  .
.
3. Conosci il significato di lunga divisione. Si noti che il metodo per calcolare la radice cubica funziona proprio come la divisione lunga. Nella divisione lunga vedi che due fattori moltiplicati insieme, dai il numero con cui hai iniziato. In questo calcolo, il numero che stai cercando (il numero che finisce sopra il radicale) è la radice cubica. Ciò significa che è uguale al termine (10A+B). Gli effettivi A e B sono irrilevanti ora, purché tu capisca la relazione con la risposta.

4. Visualizza la versione estesa. Quando guardi il binomio di Newton, vedi perché l`algoritmo della radice cubica è corretto. Guarda come il divisore in ogni passaggio dell`algoritmo è uguale alla somma dei quattro termini che devi calcolare e sommare. Questi termini sorgono come segue:
 .) Ricorda che quando si calcola la radice cubica, la prima cifra in ogni passaggio è stata moltiplicata per 0300.
.) Ricorda che quando si calcola la radice cubica, la prima cifra in ogni passaggio è stata moltiplicata per 0300.
5. Guarda Crescere la precisione. Elaborando una lunga divisione, ogni passaggio che completi fornisce una grande precisione alla tua risposta. Ad esempio, il problema di esempio elaborato in questo articolo riguarda la determinazione della radice cubica di 10. Nel primo passaggio, la soluzione è 2, perché  si avvicina, ma è inferiore a 10. Di fatto,
si avvicina, ma è inferiore a 10. Di fatto,  . Dopo il secondo round, la tua soluzione è 2.1. Una volta che avrai risolto questo problema, otterrai
. Dopo il secondo round, la tua soluzione è 2.1. Una volta che avrai risolto questo problema, otterrai , e questo è molto più vicino al risultato desiderato (10). Dopo il terzo round hai 2.15, e questo ti dà
, e questo è molto più vicino al risultato desiderato (10). Dopo il terzo round hai 2.15, e questo ti dà  . Continua a lavorare in gruppi di tre numeri e otterrai una risposta precisa quanto desideri.
. Continua a lavorare in gruppi di tre numeri e otterrai una risposta precisa quanto desideri.
 si avvicina, ma è inferiore a 10. Di fatto,
si avvicina, ma è inferiore a 10. Di fatto,  . Dopo il secondo round, la tua soluzione è 2.1. Una volta che avrai risolto questo problema, otterrai
. Dopo il secondo round, la tua soluzione è 2.1. Una volta che avrai risolto questo problema, otterrai , e questo è molto più vicino al risultato desiderato (10). Dopo il terzo round hai 2.15, e questo ti dà
, e questo è molto più vicino al risultato desiderato (10). Dopo il terzo round hai 2.15, e questo ti dà  . Continua a lavorare in gruppi di tre numeri e otterrai una risposta precisa quanto desideri.
. Continua a lavorare in gruppi di tre numeri e otterrai una risposta precisa quanto desideri.Consigli
- Come ogni cosa, le tue abilità matematiche miglioreranno con la pratica. Più ti eserciti, meglio sarai in grado di fare questo tipo di calcoli.
Avvertenze
- È facile sbagliare qui. Controlla attentamente il tuo lavoro e ripeti l`elaborazione.
Necessità
- Penna o matita
- Carta
- Governate
- Gomma
Articoli sull'argomento "Calcolo delle radici del cubo a mano"
Condividi sui social network:
Popolare