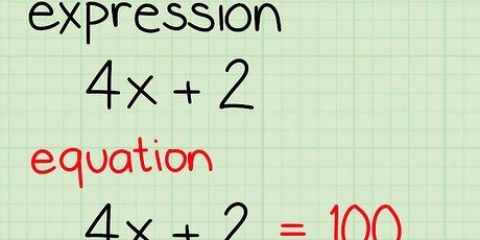Esempio: la seguente espressione 2x + 4(5 + 2) + 3 - (3 + 4/2). Per prima cosa risolvi i termini tra parentesi, quindi 5 + 2 e 3 + 4/2. 5 + 2 = 7. 3 + 4/2 = 3 + 2 = 5. Il termine tra la seconda coppia di parentesi diventa 5 perché prima dobbiamo calcolare 4/2 e solo dopo calcolare l`addizione. Se dovessimo semplicemente lavorare da sinistra a destra, la somma sarebbe 3 + 4: 2, per cui verrebbero calcolati prima 3 + 4 e poi 7 / 2, risultando nella risposta sbagliata 7/2. Nota: se sono nidificate più parentesi (parentesi tra parentesi), dissolvi prima quella interna e procedi verso le parentesi esterne. 
Dopo aver risolto le parentesi, l`esempio era simile a questo. 2x + 4(7) + 3 - 5. L`unica potenza nel nostro esempio è 3, e questo è uguale a 9. L`espressione ora diventa 2x + 4(7) + 9 - 5. 
Ci sono due moltiplicazioni nel problema: 2x (2x è 2 × x) e 4(7). Non conosciamo il valore di x, quindi lasciamolo come 2x. 4(7) = 4 × 7 = 28. Possiamo scriverlo diversamente come 2x + 28 + 9 - 5. 
Poiché abbiamo già risolto un problema di divisione che era tra parentesi, non ci sono più problemi di divisione nel nostro problema, quindi possiamo saltare questo passaggio. Ciò solleva un punto importante: se un`operazione non si verifica in un`espressione, procedere all`operazione successiva come indicato nelle regole delle regole matematiche. 
La nostra espressione è ora parzialmente semplificata in "2x + 28 + 9 - 5". Ora sommiamo il più possibile, da sinistra a destra. Non possiamo aggiungere 2x agli altri numeri, perché non conosciamo il valore di x, quindi saltiamo questo. 28 + 9 = 37, quindi possiamo riscrivere l`espressione come "2x + 37 - 5". 
Nella nostra espressione, "2x + 37 - 5", c`è solo una sottrazione,37 - 5 = 32 
La nostra risposta finale è "2x + 32". Non possiamo risolvere l`addizione senza conoscere il valore di x, ma una volta fatto, è molto più facile da risolvere rispetto all`espressione originale. 

Ad esempio, supponiamo di dover risolvere la frazione 36/60. Se abbiamo una calcolatrice a portata di mano, la risposta (6) viene calcolata in questo modo. Se non abbiamo questo, possiamo fare molto eliminando fattori simili. Un altro modo di pensare a 36/60 è come (6 × 6)/(6 × 10). Questo può essere nuovamente riscritto come 6/6 × 6/10. 6/6 = 1, quindi la nostra espressione diventa 1 × 6/10 = 6/10. Ma non ci siamo ancora: sia 6 che 10 hanno lo stesso fattore 2. Ripetendo la procedura sopra, manteniamo3/5 di. 
Supponiamo di avere l`espressione (3x + 3x)/(-3x + 15x).Questa frazione può essere riscritta come (x + 1)(3x)/(3x)(5 - x), 3x si trova sia al numeratore che al denominatore. La rimozione di questi fattori dall`equazione dà (x + 1)/(5 - x). Allo stesso modo, questo è il caso dell`equazione (2x + 4x + 6)/2. Poiché ogni termine è divisibile per 2, possiamo riscriverlo come (2(x + 2x + 3))/2 e quindi semplificare x + 2 x + 3. Intendiamoci, non puoi eliminare tutti i termini, solo quei fattori che sono sia nel numeratore che nel denominatore. Ad esempio, l`espressione (x(x + 2))/x, dove il "X" può essere rimosso dalla frazione, lasciando (x + 2)/1 = (x + 2). Ma (x + 2)/x non è per semplificare a 2/1 = 2. 
Ad esempio, l`espressione 3(x + 8 può essere semplificata in3x + 24, mentre 3x(x + 8) può essere semplificato in 3x + 24x. Si noti che in alcuni casi, come con le frazioni variabili, la costante fuori dalle parentesi può essere utilizzata nella semplificazione e quindi non deve essere moltiplicata. Ad esempio, nella frazione (3(x + 8))/3x, il fattore 3 è sia al numeratore che al denominatore, quindi possiamo cancellarlo e semplificare l`espressione in (x + 8)/x. Questo è più semplice e facile da lavorare rispetto a (3x + 24x)/3x, che sarebbe stata la risposta se avessimo moltiplicato. 
Dai un`altra occhiata all`espressione x - 5x + 6. Questo può essere risolto in (x - 3)(x - 2). Quindi se x - 5x + 6 è il numeratore di un`equazione con uno di questi fattori al denominatore (come in (x - 5x + 6)/(2(x - 2))), allora possiamo scomporrlo in fattori come che possiamo eliminare il denominatore. In altre parole, a (x - 3)(x - 2)/(2(x - 2)), (x - 2) cade, lasciandoci(x - 3)/2 rimasto. Come indicato sopra, puoi anche risolvere un`equazione con la fattorizzazione, soprattutto se posta uguale a zero. Ad esempio: prendi l`equazione x - 5x + 6 = 0. Il factoring ci dà (x - 3)(x - 2) = 0. Poiché un numero per zero è uguale a zero, possiamo porre entrambi i termini uguali a zero, per trovare la risposta a questo problema. Quindi la risposta all`equazione è x=3 e x= 2.
Semplificare le espressioni matematiche
Contenuto
I problemi di matematica spesso richiedono una risposta "il più semplice possibile" scrivere, in altre parole, dare una risposta nel modo più elegante possibile. Mentre un`espressione lunga e goffa e una versione più breve ed elegante di essa tecnicamente significano la stessa cosa, una risposta spesso non viene accettata finché non è stata semplificata il più possibile.Inoltre, è anche più facile lavorare con le risposte semplificate. `Ecco perché imparare a semplificare è un`abilità essenziale per i futuri matematici.
Passi
Metodo 1 di 2: L`ordine delle operazioni matematiche

1. L`ordine delle operazioni. Quando semplifichi le espressioni matematiche, non puoi semplicemente valutare da sinistra a destra. Alcune operazioni hanno la precedenza su altre e devono quindi essere eseguite per prime. Se non lo fai, potresti ottenere la risposta sbagliata. L`ordine delle operazioni in matematica è il seguente: parentesi, esponenziale e rooting, moltiplicazione e divisione, addizione e sottrazione. Un mnemonico per ricordare questa sequenza è "Come dovremmo sbarazzarci dell`inadeguato " o "HMWVDOA".
- Si noti che mentre una conoscenza di base delle operazioni è sufficiente per risolvere la maggior parte delle espressioni standard, sono necessarie tecniche speciali per risolvere espressioni contenenti variabili, inclusa la maggior parte dei polinomi. Guarda il Metodo Due per ulteriori informazioni.

2. Inizia risolvendo tutti i termini tra parentesi. In matematica, le parentesi significano che tutti i termini che racchiudono devono essere risolti separatamente dall`espressione circostante. Indipendentemente dalle operazioni, assicurati di risolvere prima tutti i termini tra parentesi se desideri semplificare un`espressione. Tieni presente che le regole di calcolo per l`ordine delle operazioni si applicano anche tra parentesi. Quindi anche qui prima le parentesi, poi l`esponenziazione, ecc.

3. Ora dissolvi i poteri. Dopo aver elaborato le parentesi, ora puoi passare all`esponenziazione. Risolvili uno per uno.

4. Ora risolvi le moltiplicazioni. Ricorda che una moltiplicazione può essere scritta in diversi modi. Con un punto, senza un punto o con un simbolo ×. Ma anche qualcosa di simile 4(x)) indica una moltiplicazione.

5. Continua con i problemi di divisione. Se stai cercando problemi di divisione, ricorda che anche questi possono essere scritti in modi diversi. Il semplice simbolo ÷ , con due punti o una barra (come 3/4) indicano tutti una divisione.

6. Addizionare. Ora somma i diversi termini. Risolvilo da sinistra a destra, come è nell`espressione e qualunque sia il più conveniente. Ad esempio, nella somma 49 + 29 + 51 +71, è più facile dividere il problema nei seguenti blocchi: 49 + 51 = 100, 29 + 71 = 100 e 100 + 100 = 200. Questo è più facile di 49 + 29 = 78, 78 + 51 = 129 e 129 + 71 = 200.

7. sottrarre. L`ultimo passaggio delle operazioni consiste nel sottrarre i termini rimanenti. Elabora il resto della tua espressione, da sinistra a destra. Puoi aggiungere numeri negativi in questo o nel passaggio precedente, non importa per la tua risposta.

8. Guarda la tua espressione. Dopo aver elaborato la sequenza delle operazioni, ti rimangono una serie di termini nella forma più semplificata. Se sono presenti una o più variabili nell`espressione, rimangono sostanzialmente invariate. Semplificare le espressioni con le variabili richiede di risolvere ulteriormente queste equazioni per le incognite o di utilizzare metodi speciali (vedi passaggio successivo).
Metodo 2 di 2: Semplificare le espressioni complesse

1. Somma potenze variabili uguali insieme. Quando si tratta di espressioni che contengono variabili, è importante ricordare che i termini con la stessa variabile e lo stesso esponente (o "Condizioni uguali") possono essere sommati (o sottratti) come numeri regolari. I termini dovere non solo hanno la stessa variabile, ma anche lo stesso esponente. Ad esempio, 7x e 5x possono essere sommati, ma 7x e 5x no.
- Questa regola può essere estesa anche a termini multivariati. Ad esempio, 2xy può essere aggiunto a -3xy, ma non -3xy o -3y.
- Prendi le seguenti espressioni:x + 3x + 6 - 8x. In questa espressione, possiamo sommare i termini 3x e -8x perché sono uguali tra loro. La nostra espressione diventa quindi semplificata: x - 5 x + 6.

2. Semplifica le frazioni eliminando o dividendo i fattori. Le frazioni che consistono solo di numeri (e non di variabili) possono essere semplificate in diversi modi. Una frazione è solo una somma di divisione e dovrebbe essere trattata come tale. Inoltre, se la stessa moltiplicazione si verifica al numeratore o al denominatore, può essere eliminata, perché danno già risposta 1 quando condivisa. In altre parole, se numeratore e denominatore hanno entrambi lo stesso fattore, allora può essere rimosso dalla frazione, semplificando il risultato.

3. Se hai a che fare con frazioni che contengono variabili, prova ad eliminare le variabili. Queste espressioni offrono possibilità uniche di semplificazione. Come le frazioni regolari, le frazioni variabili consentono di rimuovere i fattori che si trovano sia nel numeratore che nel denominatore. Ma in quest`ultimo caso, questi fattori possono essere numeri oltre che variabili.

4. Moltiplica i termini tra parentesi per le loro costanti. Quando si tratta di termini variabili tra parentesi più una costante, la moltiplicazione di qualsiasi termine tra parentesi per la costante al di fuori delle parentesi può risultare in un`espressione più semplice.Questo vale sia per le costanti numeriche che per le costanti con variabili.

5. Semplificare con il factoring. Questa è una tecnica che può semplificare alcune equazioni. Quando fai il factor, pensa a qualcosa che è l`opposto di "moltiplicando le parentesi" – a volte un`equazione può essere rappresentata più semplicemente come due termini moltiplicati insieme che come un`unica equazione. Ciò è particolarmente vero se puoi eliminare parte dell`equazione con esso. In alcuni casi (come con le equazioni di secondo grado) puoi anche risolvere l`equazione stessa con la fattorizzazione.
Articoli sull'argomento "Semplificare le espressioni matematiche"
Condividi sui social network:
Simile
Popolare