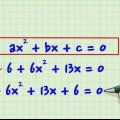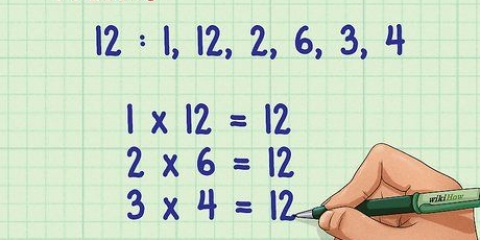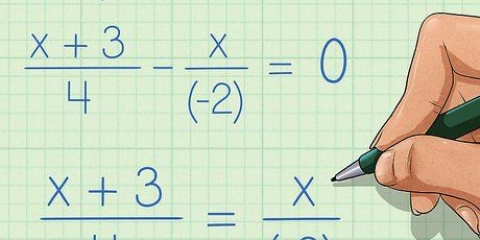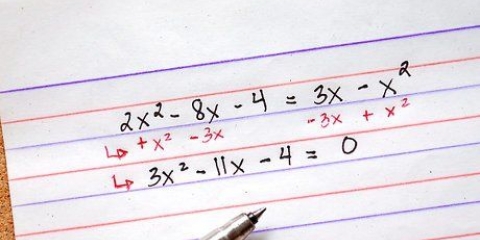Ad esempio: se vuoi dividere 20 in fattori, puoi scriverlo come 4×5. Si noti che i termini variabili possono anche essere scritti come fattori. - Ad esempio, 20x può essere scritto come 4(5x). I numeri primi non possono essere scritti come fattori perché sono divisibili solo per se stessi e per 1. 
ehpipistrelli malza otto wcontrazione Vmoltiplicare Delena ocontare unsottrarre 

Per esempio, troviamo i termini simili nella nostra equazione 1 + 2x - 3 + 4x. 2x e 4x hanno entrambi la stessa variabile elevata alla stessa potenza (in questo caso, le variabili x non hanno alcun esponente). Inoltre, 1 e -3 sono termini uguali, perché nessuno dei due ha una variabile. Quindi in questa equazione sono 2x e 4x e 1 e-3 Condizioni uguali. 
Aggiungiamo insieme i termini uguali nel nostro esempio. 2x + 4x = 6x 1 + -3 = -2 
Nel nostro esempio, i termini semplificati erano 6x e -2, quindi la nuova espressione diventa 6x - 2. Questa espressione semplificata è equivalente all`originale (1 + 2x - 3 + 4x), ma è più breve e più facile da calcolare con. È più facile scomporre, che, come vedremo di seguito, è un`abilità importante per poter semplificare. 
Ad esempio, supponiamo di avere l`equazione 5(3x-1) + x((2x)/(2)) + 8 - 3x. Quindi non sarebbe corretto considerare immediatamente 3x e 2x come termini uguali e combinarli, perché le parentesi nell`espressione indicano che dobbiamo prima fare altre operazioni. Per prima cosa, eseguiamo le operazioni aritmetiche nell`espressione secondo l`ordine delle operazioni, per ottenere i termini che abbiamo bene poter usare. Vedi sotto: 5(3x-1) + x((2x)/(2)) + 8 - 3x 15x - 5 + x(x) + 8 - 3x 15x - 5 +x + 8 - 3x. passaggio Ora poiché le uniche operazioni rimaste sono addizione e sottrazione, possiamo combinare i termini simili. x + (15x - 3x) + (8 - 5) x + 12 x + 3 

Analizziamo la nostra equazione usando il massimo comun divisore, 3. Lo facciamo dividendo ogni termine per 3. 9x/3 = 3x 27x/3 = 9x -3/3 = -1 Quindi la nuova espressione è 3x + 9x - 1. 
Per la nostra espressione di esempio, 3x + 9x - 1, mettiamo l`espressione tra parentesi e moltiplichiamo questo termine per il massimo comun divisore dell`equazione originale da convertire 3(3x + 9x - 1) ottenere. Questa equazione è equivalente all`originale, 9x + 27x - 3. 
Supponiamo che la nostra espressione di esempio originale, 9x + 27x - 3, sia uguale al numeratore di una frazione maggiore con 3 come denominatore. Questa frazione si presenta così: (9x + 27x - 3)/3. Possiamo usare la fattorizzazione per semplificare questa frazione. Aggiungi la forma fattorizzata della nostra espressione originale al numeratore: (3(3x + 9x - 1))/3 Si noti che sia il numeratore che il denominatore hanno 3 come coefficiente. Se dividi numeratore e denominatore per 3, ottieni: (3x + 9x - 1)/1. Perché una frazione con "1" al denominatore è uguale ai termini al numeratore, possiamo dire che la nostra frazione originaria può essere semplificata in 3x + 9x - 1. 

Facciamo un semplice esempio: √(90). Se prendiamo il numero 90 come prodotto dei due fattori, 9 e 10, possiamo calcolare la radice quadrata di 9 per ottenere 3 e metterlo davanti al radicale. In altre parole: (90) √(9×10) (√(9) × √(10)) 3 × √(10) 3√(10) 
Ad esempio, supponiamo di avere l`espressione 6x × 8x + (x/x). In ogni caso dove è necessario moltiplicare o dividere esponenti, sottraiamo o aggiungiamo rispettivamente gli esponenti, per risolvere velocemente un termine semplificato. Vedi sotto: 6x × 8x + (x/x) (6×8)x + (x) 48x+x Per una spiegazione, vedere di seguito: Moltiplicare termini esponenziali equivale essenzialmente a moltiplicare lunghe serie di termini senza esponenti. Ad esempio, perché x = x × x × x e x= x × x × x × x × x, x × x = (x × x × x) × (x × x × x × x × x) o x. Allo stesso modo, dividere termini esponenziali equivale a dividere lunghe sequenze di termini senza esponenti. x/x = (x × x × x × x × x)/(x × x × x). Poiché qualsiasi termine al numeratore può essere cancellato rispetto allo stesso termine al denominatore, ci rimane il doppio di una x al numeratore e nessuno al denominatore, lasciandoci con x come risposta.
Semplificare le equazioni matematiche
Contenuto
Essere in grado di semplificare le equazioni algebriche è una parte essenziale della padronanza delle basi dell`algebra e uno strumento estremamente prezioso per tutti i matematici. La semplificazione consente a un matematico di cambiare un`espressione complessa, lunga e/o goffa in una forma più semplice o più conveniente ma equivalente. Le basi della semplificazione sono abbastanza facili da imparare, anche per chi odia la matematica. Seguendo alcuni semplici passaggi è possibile semplificare molte delle più comuni espressioni algebriche senza particolari conoscenze matematiche.
Passi
Metodo 1 di 4: Comprensione dei concetti chiave

1. Determinare "Condizioni uguali" secondo le loro variabili e poteri. Possedere in algebra "Condizioni uguali" sulle stesse variabili, elevato alla stessa potenza. In altre parole, due termini sono "simile", quando hanno le stesse variabili, o nessuna, e quando ogni variabile ha la stessa potenza, o nessuna. L`ordine delle variabili all`interno di un termine non ha importanza.
- Ad esempio, 3x e 4x sono termini uguali perché ogni termine ha una variabile x elevata alla seconda potenza. Le variabili x e x non sono termini uguali, perché x ha una potenza diversa in ogni termine. Allo stesso modo, -3yx e 5xz non sono termini uguali, perché ogni termine è composto da variabili diverse.

2. Fattorizza scrivendo i numeri come il prodotto di due fattori. La fattorizzazione è un modo per scrivere un dato numero come prodotto di due fattori. I numeri possono essere costituiti da più fattori, ad esempio il numero 12, che può essere formato da 1 × 12, 2 × 6 e 3 × 4, in modo che possiamo dire che 1, 2, 3, 4, 6, e 12 sono tutti fattori di 12. Un altro modo di vederlo è che i fattori di un numero sono i numeri per i quali è divisibile.

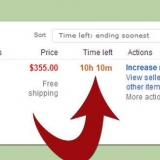
3. Usa il mnemonico `Come dovremmo sbarazzarci delle inadeguatezze` (o come acronimo HMWVDOA) per ricordare l`ordine delle operazioni. A volte semplificare un`espressione significa semplicemente eseguire le operazioni nell`espressione finché non è possibile fare altro. In tal caso è importante conoscere l`ordine delle operazioni, per evitare errori di calcolo. Questo mnemonico può aiutarti a ricordare l`ordine delle modifiche: le lettere corrispondono al tipo di modifiche che devi eseguire e in quale ordine. Se ci sono moltiplicazioni e divisioni nello stesso problema, dovrai eseguire quelle operazioni da sinistra a destra quando arrivi a quel punto. Lo stesso vale per addizione e sottrazione. L`immagine sopra dà una risposta che non è corretta. L`ultimo passaggio non ha funzionato addizione e sottrazione da sinistra a destra. Per prima cosa è stato aggiunto. Dovrebbero esserci 25 - 20 = 5 e poi 5 + 6 = 11.
Metodo 2 di 4: Combinazione di termini simili

1. Scrivi le tue equazioni. Le equazioni matematiche più semplici (quelle con poche variabili e coefficienti come numeri interi, senza frazioni, radici quadrate, ecc.) spesso possono essere risolti in pochi passaggi. Come per la maggior parte dei problemi di matematica, il primo passo per semplificare un`equazione è scrivere l`equazione!
- Per i prossimi passi prendiamo l`espressione 1 + 2x - 3 + 4x come esempio.

2. Determina quali sono i termini simili. Ora cerca i termini simili nella tua equazione. Ricorda che termini simili hanno entrambi le stesse variabili ed esponenti.

3. Combina termini simili. Ora che hai determinato i termini simili, puoi iniziare a combinarli per semplificare la tua equazione. Somma i termini insieme (o sottraili nel caso di termini negativi) per semplificare ogni insieme di termini (con le stesse variabili ed esponenti) in un termine.

4. Fai un`espressione semplificata dei tuoi termini semplificati. Dopo aver combinato i tuoi termini simili, costruisci un`espressione dal tuo nuovo insieme più piccolo di termini. Ora dovresti avere un`espressione più semplice con un termine per ogni insieme di variabili ed esponenti nell`espressione originale. Questa nuova espressione è equivalente alla prima.

5. Rispettare l`ordine delle operazioni quando si combinano termini simili. In espressioni molto semplici come quelle di cui ci siamo occupati negli esercizi precedenti, riconoscere i termini simili è facile. Nelle espressioni più complesse, come quelle con termini tra parentesi, frazioni e radici, la combinazione di termini simili non sarà immediatamente evidente. In questi casi, segui la sequenza delle operazioni ed esegui le operazioni sui termini nella tua espressione finché non ti rimangono solo addizioni e sottrazioni.
Metodo 3 di 4: Factoring

1. Trova il massimo comun divisore nell`espressione. Il factoring è un modo per semplificare le espressioni rimuovendo i fattori che appaiono in tutti i termini dell`espressione. Per iniziare, trova il massimo comun divisore di tutti i termini nell`espressione, in altre parole, il numero massimo per cui tutti i termini nell`espressione sono divisibili per.
- Supponiamo di prendere l`equazione 9x + 27x - 3. Nota che ogni termine in questa equazione è divisibile per 3. Perché no dei termini è completamente divisibile per un altro numero più grande, possiamo dirlo 3 è il massimo comune denominatore della nostra espressione.

2. Dividi i termini dell`espressione per il massimo comun divisore. Quindi dividi ogni termine nella tua equazione per il massimo comun divisore che hai appena trovato. I termini risultanti avranno tutti coefficienti più piccoli rispetto a quelli dell`espressione originale.

3. Scrivi la tua espressione come il prodotto del massimo comun divisore e dei termini rimanenti. La tua nuova espressione non è la stessa di quella vecchia, quindi non è corretto dire che è la versione semplificata. Per rendere la nuova espressione uguale alla vecchia, dovremo tenere conto che è divisa per il massimo comun divisore. Metti la tua nuova espressione tra parentesi e scrivi il massimo comun divisore dell`equazione originale come coefficiente dell`espressione anche tra parentesi.

4. Fattore per semplificare le frazioni. Ti starai ora chiedendo perché la fattorizzazione è utile se la nuova espressione deve essere moltiplicata di nuovo dopo aver rimosso il massimo comun divisore. Il factoring consente a un matematico di utilizzare una serie di trucchi per semplificare un`espressione. Uno dei più semplici di questi trucchi utilizza il fatto che moltiplicando il numeratore e il denominatore di una frazione per lo stesso numero si ottiene una frazione con le stesse proporzioni. Vedi sotto:
Metodo 4 di 4: Applica semplifica

1. Semplifica le frazioni dividendo per fattori uguali. Come accennato in precedenza, se numeratore e denominatore di un`espressione hanno gli stessi fattori, questi fattori possono essere rimossi dalla frazione. A volte ciò richiede che il numeratore, il denominatore o entrambi siano fattorizzati (come nel caso dell`esempio sopra), mentre in altri casi i fattori condivisi sono immediatamente evidenti. Si noti che è anche possibile dividere i singoli termini al numeratore per l`espressione al denominatore, per ottenere un`espressione semplificata.
- Affrontiamo un esempio che non richiede necessariamente di scriverli per semplificare. Supponiamo di avere la frazione (5x + 10x + 20)/10, puoi dividere ogni termine al numeratore per il 10 al denominatore, per semplificare il tutto, anche se il "5" in 5x non maggiore di 10 e non è possibile scegliere 10 come fattore.
- In questo modo otteniamo ((5x)/10) + x + 2. Se vogliamo, possiamo riscrivere il primo termine come (1/2)x per ottenere (1/2)x + x + 2.

2. Usa le radici quadrate per semplificare le radici. Le espressioni sotto il segno di una radice quadrata sono dette equazioni di radice quadrata. Puoi semplificarlo determinando le radici quadrate (fattori che a loro volta formano una seconda potenza di un intero), dopodiché sottrai la radice quadrata di questi fattori per rimuoverli dal segno radicale.

3. Somma gli esponenti quando moltiplichi due termini esponenziali e sottraili quando dividi. Alcune equazioni algebriche richiedono la moltiplicazione o la divisione di termini esponenziali. Non elabori ogni termine esponenziale e non moltiplichi o dividi manualmente, ma contare si sommano gli esponenti di ogni termine moltiplicandoli insieme e li tiri? quando li condividi, risparmiando molto tempo. Puoi anche applicare questo concetto per semplificare le equazioni con più variabili.
Consigli
- Ricorda che devi considerare questi numeri come positivi o negativi. Molte persone si bloccano con questo e pensano, "Che segno dovrei mettere qui?"
- Chiedi aiuto se ne hai bisogno!
- Semplificare le equazioni matematiche non è facile, ma una volta presa la mano, puoi usarla per il resto della tua vita.
Avvertenze
- Fai attenzione a non aggiungere accidentalmente alcuni numeri, esponenti o operazioni extra che non appartengono a questo.
- Presta sempre attenzione alla parità di condizioni e non lasciarti ingannare dagli esponenti.
Articoli sull'argomento "Semplificare le equazioni matematiche"
Condividi sui social network:
Popolare