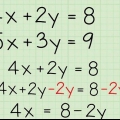2x - 2x = 0 4 anni - 2 anni = 2 anni 8 - 2 = 6 2x + 4a = 8-(2x + 2a = 2)=0 +2a = 6 
2 anni = 6 Dividi 2y e 6 per 2 e ottieni y = 3 
Inserisci y = 3 nell`equazione 2x + 2y = 2 e risolvi per x. 2x + 2(3) = 2 2x + 6 = 2 2x = -4 x = - 2 Hai risolto il sistema di equazioni per sottrazione. (x, y) = (-2, 3) 
Completa (-2, 3) per (x, y) nell`equazione 2x + 4y = 8. 2(-2) + 4(3) = 8 -4 + 12 = 8 8 = 8 Completa (-2, 3) per (x, y) nell`equazione 2x + 2y = 2. 2(-2) + 2(3) = 2 -4 + 6 = 2 2 = 2 

3x + x = 4x 6 anni + -6 anni = 0 8 + 4 = 12 Se combini questo ottieni un nuovo prodotto: 3x + 6 anni = 8 +(x - 6y = 4) = 4x + 0 = 12 
4x + 0 = 12 4x = 12 Dividi 4x e 12 per 3 per ottenere x = 3 
Inserisci x = 3 nell`equazione x - 6y = 4 per trovare y. 3 - 6 anni = 4 -6 anni = 1 Dividi -6y e 1 per -6 per ottenere y = -1/6. Hai risolto il sistema di equazioni con l`addizione. (x, y) = (3, -1/6) 
Completa (3, -1/6) per (x, y) nell`equazione 3x + 6y = 8. 3(3) + 6(-1/6) = 8 9 - 1 = 8 8 = 8 Completa (3, -1/6) per (x, y) nell`equazione x - 6y = 4. 3 - (6 * -1/6) =4 3 - - 1 = 4 3 + 1 = 4 4 = 4 

2 (2x - y = 2) 4x - 2 anni = 4 
3x + 2 anni = 10 + 4x - 2 anni = 4 7x + 0 = 14 7x = 14 

x = 2 ---> 2x - y = 2 4 - y = 2 -y = -2 y = 2 Hai risolto il sistema di equazioni usando la moltiplicazione. (x, y) = (2, 2) 
Completa (2, 2) per (x, y) nell`equazione 3x + 2y = 10. 3(2) + 2(2) = 10 6 + 4 = 10 10 = 10 Completa (2, 2) per (x, y) nell`equazione 2x - y = 2. 2(2) - 2 = 2 4 - 2 = 2 2 = 2 

x = 2 - 4 anni --> 2x + 3 anni = 9 2(2 - 4 anni) + 3 anni = 9 4 - 8 anni + 3 anni = 9 4 - 5 anni = 9 -5 anni = 9 - 4 -5 anni = 5 -y = 1 y = - 1 
y = -1 --> x = 2 - 4 anni x = 2 - 4(-1) x = 2 - -4 x = 2 + 4 x = 6 Hai risolto il sistema di equazioni usando la sostituzione. (x, y) = (6, -1) 
Completa (6, -1) per (x, y) nell`equazione 2x + 3y = 9. 2(6) + 3(-1) = 9 12 - 3 = 9 9 = 9 Completa (6, -1) per (x, y) nell`equazione x + 4y = 2. 6 + 4(-1) = 2 6 - 4 = 2 2 = 2
Risolvere un sistema di equazioni
Contenuto
La risoluzione di un sistema di equazioni richiede di trovare il valore di più variabili in più equazioni. Puoi risolvere un sistema di equazioni usando addizioni, sottrazioni, moltiplicazioni o sostituzioni. Se desideri imparare a risolvere un sistema di equazioni, tutto ciò che devi fare è seguire questi passaggi.
Passi
Metodo 1 di 4: Risolvi per sottrazione

1. Scrivi un`equazione sull`altra. Risolvere queste equazioni con la sottrazione è un metodo ideale se vedi che entrambe le equazioni hanno la stessa variabile con lo stesso coefficiente e segno. Ad esempio, se entrambe le equazioni hanno la variabile -2x, puoi utilizzare la sottrazione per trovare il valore di entrambe le variabili.
- Scrivi un`equazione sopra l`altra in modo che le variabili xey di entrambe le equazioni e dei numeri siano una sotto l`altra. Metti il segno meno accanto al numero in basso.
- Ad esempio: se hai le seguenti due equazioni: 2x + 4y = 8 e 2x + 2y = 2, sarebbe simile a questa:
- 2x + 4 anni = 8
- -(2x + 2y = 2)

2. Sottrai termini simili. Ora che le due equazioni sono allineate, tutto ciò che devi fare è sottrarre i termini simili. Fallo con un termine alla volta:

3. Risolvi per il termine rimanente. Rimuovi qualsiasi zero dall`equazione che è stata creata, non cambia il valore e risolvi l`equazione rimanente.

4. Immettere il valore trovato della variabile in una delle equazioni. Ora che sai che y = 3, puoi inserire questo valore nell`equazione originale per risolvere x. Non importa quale equazione scegli, la risposta è la stessa. Quindi usa l`equazione più semplice!

5. Controlla la tua risposta. Per assicurarti che la tua risposta sia corretta, inserisci entrambe le risposte in entrambe le equazioni. Ecco come farlo:
Metodo 2 di 4: Risolvi per addizione

1. Scrivi un`equazione sull`altra. Risolvere un sistema di equazioni per addizione è il metodo migliore, se si nota che entrambe le equazioni hanno una variabile con lo stesso coefficiente, ma con segno diverso; ad esempio, se un`equazione contiene la variabile 3x e l`altra la variabile -3x.
- Scrivi un`equazione sopra l`altra in modo che le variabili xey di entrambe le equazioni e dei numeri siano una sotto l`altra. Metti il segno più accanto al numero in basso.
- Ad esempio: hai le seguenti due equazioni 3x + 6y = 8 e x - 6y = 4, quindi scrivi la prima equazione sopra la seconda come mostrato di seguito:
- 3x + 6 anni = 8
- +(x - 6y = 4)

2. Aggiungi termini simili insieme. Ora che le due equazioni sono allineate una sopra l`altra, tutto ciò che devi fare è sommare i termini con la stessa variabile:

3. Risolvi per il termine rimanente. Rimuovi qualsiasi zero dall`equazione che è sorta, non cambia il valore. Risolvi l`equazione rimanente.

4. Immettere il valore trovato di questa variabile in una delle equazioni. Ora che sai che x = 3, puoi inserire questo valore nell`equazione originale per risolvere per y. Non importa quale equazione scegli, la risposta è la stessa. Quindi usa l`equazione più semplice!

5. Controlla la tua risposta. Per assicurarti che la tua risposta sia corretta, inserisci entrambe le risposte in entrambe le equazioni. Ecco come farlo:
Metodo 3 di 4: Risolvi per moltiplicazione

1. Scrivi un`equazione sull`altra. Scrivi un`equazione sopra l`altra in modo che le variabili xey di entrambe le equazioni e dei numeri siano una sotto l`altra. Se stai usando la moltiplicazione, lo stai facendo perché nessuna delle variabili ha coefficienti uguali - in questo momento.
- 3x + 2 anni = 10
- 2x - y = 2

2. Garantire coefficienti uguali. Quindi moltiplica una o entrambe le equazioni per un numero, in modo che una delle variabili abbia lo stesso coefficiente. In questo caso, puoi moltiplicare l`intera seconda equazione per 2 in modo che -y sia uguale a -2y e quindi il primo coefficiente y. Ecco come farlo:

3. Aggiungi o sottrai le equazioni. Ora tutto ciò che devi fare è eliminare i termini uguali aggiungendo o sottraendo. Dato che qui hai a che fare con 2y e -2y, ha senso usare il metodo di addizione perché è uguale a 0. Se hai a che fare con 2y + 2y, usa il metodo di sottrazione. Ecco un esempio di come utilizzare il metodo di addizione per eliminare le variabili:

4. Risolvi questo per il periodo rimanente. Questo è facilmente risolvibile trovando il valore del termine che non hai ancora eliminato. Se 7x = 14, allora x = 2.

5. Immettere il valore trovato in una delle equazioni. Immettere il termine in una delle equazioni originali da risolvere per l`altro termine. Scegli l`equazione più semplice per questo, questa è la più veloce.

6. Controlla la tua risposta. Per assicurarti che la tua risposta sia corretta, inserisci entrambe le risposte in entrambe le equazioni. Ecco come farlo:
Metodo 4 di 4: Risolvi per Sostituzione

1. Isolare una variabile. La sostituzione è ideale quando uno dei coefficienti in una delle equazioni è uguale a 1. Quindi tutto ciò che devi fare è isolare questa variabile su un lato dell`equazione per trovarne il valore.
- Se stai lavorando con le equazioni 2x + 3y = 9 e x + 4y = 2, allora devi isolare x nella seconda equazione.
- x + 4y = 2
- x = 2 - 4 anni

2. Inserisci il valore della variabile che hai isolato nell`altra equazione. Prendi il valore della variabile isolata e inseriscilo nell`altra equazione. Ovviamente non nella stessa equazione altrimenti non risolverai nulla. Ecco un esempio di come farlo:

3. Risolvi per la variabile rimanente. Ora che sai che y = - 1, inserisci questo valore nell`equazione più semplice per trovare il valore di x. Ecco un esempio di come farlo:

4. Controlla la tua risposta. Per assicurarti che la tua risposta sia corretta, inserisci entrambe le risposte in entrambe le equazioni. Ecco come farlo:
Consigli
- Ora dovresti essere in grado di risolvere qualsiasi sistema lineare di equazioni usando addizione, sottrazione, moltiplicazione o sostituzione, ma di solito un metodo è il più adatto a seconda delle equazioni.
Articoli sull'argomento "Risolvere un sistema di equazioni"
Condividi sui social network:
Simile
Popolare