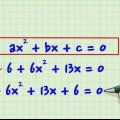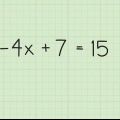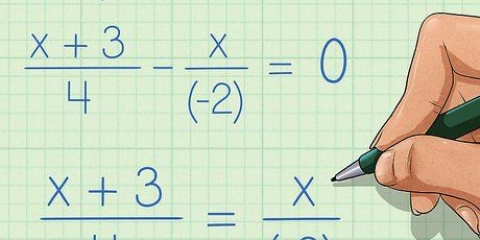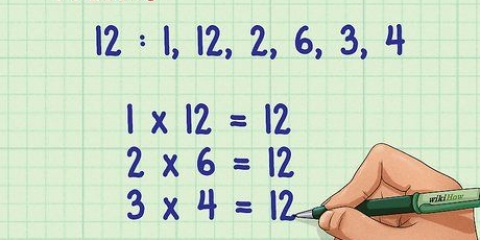Poiché 3x ha un numero finito di fattori possibili, 3x e x, puoi scriverli tra parentesi: (3x +/- ? )(x +/-- ?) = 0. Quindi usa un metodo di eliminazione in cui usi i fattori di 4 per trovare una combinazione che dia -11x come risultato della moltiplicazione. Puoi usare una combinazione di 4 e 1, o 2 e 2, perché la moltiplicazione di entrambe le combinazioni di numeri produce 4. Tieni presente che uno dei termini deve essere negativo, perché il termine è -4. Prova (3x +1)(x -4). Quando lo risolvi, ottieni - 3x -12x +x -4. Se combini i termini -12x e x ottieni -11x, che è il termine medio a cui volevi arrivare. Ora hai scomposto questa equazione quadratica. Un altro esempio; proviamo a fattorizzare un`equazione che non funziona: (3x-2)(x+2) = 3x +6x -2x -4. Se combini questi termini, ottieni 3x -4x -4. Anche se il prodotto di -2 e 2 è uguale a -4, il termine medio non funziona perché stavi cercando -11x, non -4x. 

3x + 1 = 0 = 3x = -1 = 3x/3 = -1/3 x = -1/3 x - 4 = 0 x = 4 x = (-1/3, 4) 

Quindi entrambe le soluzioni funzionano separatamente ed entrambe sono verificate come funzionanti e sono corrette in due diverse soluzioni. 



{-b +/-√ (b - 4ac)}/2 {-(-5) +/-√ ((-5) - 4(3)(-8))}/2(3) = {-(-5) +/-√ ((-5) - (-96))}/2(3) 
{-(-5) +/-√ ((-5) - (-96))}/2(3) = {5 +/-√(25 + 96)}/6 {5 +/-√(121)}/6 

(5 + 11)/6 (5 - 11)/6 
(5 + 11)/6 = 16/6 (5-11)/6 = -6/6 
16/6 = 8/3 -6/6 = -1 x = (-1, 8/3) 

2x - 12x - 9 = 0 2x - 12x = 9 
2x/2 - 12x/2 = 9/2 = x - 6 x = 9/2 
-6/2 = -3 = (-3) = 9 = x - 6 x + 9 = 9/2 + 9 


x = 3 +(√6)/2 x = 3 - (√6)/2)
Risolvi equazioni quadratiche
Contenuto
Un`equazione quadratica è un`equazione in cui l`esponente più grande di una variabile è due. Tre dei metodi più comunemente usati per risolvere queste equazioni sono: fattorizzare, usare la formula abc o dividere il quadrato. Se vuoi sapere come padroneggiare questi metodi, segui questi passaggi.
Passi
Metodo 1 di 3: Factoring

1. Sposta tutti i termini su un lato dell`equazione. Il primo passo nel factoring è spostare tutti i termini su un lato dell`equazione, lasciando x positivo. Applicare l`operazione di addizione o sottrazione ai termini x, alla variabile x e alle costanti, spostandoli su un lato dell`equazione in questo modo, senza lasciare nulla sull`altro lato. Ecco come funziona:
- 2x - 8x - 4 = 3x - x =
- 2x +x - 8x -3x - 4 = 0
- 3x - 11x = 0

2. Fattorizza l`espressione. Per fattorizzare l`espressione è necessario scomporre i fattori di 3x e i fattori della costante -4, per moltiplicarli e quindi sommarli per dare il valore del termine medio, -11. Ecco come farlo:

3. Determina che ogni coppia di parentesi è uguale a zero e trattali come equazioni separate. Questo ti fa trovare due valori per x che entrambi rendono l`intera equazione uguale a zero. Ora che hai scomposto l`equazione, tutto ciò che resta da fare è rendere ogni coppia di parentesi uguale a zero. Quindi puoi scrivere che: 3x +1 = 0 e x - 4 = 0.

4. Risolvi ogni equazione. In un`equazione quadratica ci sono due valori dati per x. Risolvi ogni equazione separatamente isolando la variabile e scrivi i risultati di x. Ecco come va:

5. Controllare x = -1/3 di pollice (3x + 1)(x – 4) = 0:
Noi abbiamo (3[-1/3] + 1)([-1/3] – 4) ?=? 0 ..... sostituendo:(-1 + 1)(-4 1/3) ?=? 0 ..... semplificando:(0)(-4 1/3) = 0 ..... moltiplicando: quindi 0=0 ..... Sì, x = -1/3 funziona
Noi abbiamo (3[-1/3] + 1)([-1/3] – 4) ?=? 0 ..... sostituendo:(-1 + 1)(-4 1/3) ?=? 0 ..... semplificando:(0)(-4 1/3) = 0 ..... moltiplicando: quindi 0=0 ..... Sì, x = -1/3 funziona

6. Controllare x = 4 pollici (3x + 1)(x - 4) = 0:
Otteniamo (3[4] + 1)([4] – 4) ?=? 0..... sostituendo:(13)(4 – 4) ?=? 0 ..... attenuando:(13)(0) = 0 ..... moltiplicando: 0=0 ..... Sì, x = 4 opere
Otteniamo (3[4] + 1)([4] – 4) ?=? 0..... sostituendo:(13)(4 – 4) ?=? 0 ..... attenuando:(13)(0) = 0 ..... moltiplicando: 0=0 ..... Sì, x = 4 opere
Metodo 2 di 3: Applicazione della formula Abc

1. Sposta tutti i termini su un lato dell`equazione e unisci i termini simili. Sposta tutti i termini su un lato del segno di uguale, mantenendo il termine x positivo. Scrivi i termini in ordine di grandezza decrescente, quindi x viene prima seguito da x, poi dalla costante. Ecco come farlo:
- 4x - 5x - 13 =x -5
- 4x - x - 5x - 13 +5 = 0
- 3x - 5x - 8 = 0

2. Scrivi la formula abc. Questo è: {-b +/-√ (b - 4ac)}/2a

3. Determina i valori di a, b e c nell`equazione quadratica. La variabile un è il coefficiente di x, B è il coefficiente di x e C è la costante. Per l`equazione 3x -5x - 8 = 0, a = 3, b = -5 e c = -8. Annota questo.

4. Sostituisci i valori di a, b e c nell`equazione. Ora che conosci i valori delle tre variabili, puoi semplicemente inserirli nell`equazione come mostriamo qui:

5. Calcolare. Dopo aver inserito i numeri, risolvi ulteriormente il problema. Di seguito puoi leggere come va oltre:

6. Semplifica la radice quadrata. Se il numero sotto il segno radicale è un quadrato perfetto o anche un numero quadrato, allora ottieni un numero intero con radice quadrata. In altri casi, semplifica il più possibile la radice quadrata. Se il numero è negativo e sei sicuro che questa sia l`intenzione, la radice quadrata del numero sarà meno semplice. In questo esempio, √(121) = 11. Puoi quindi scrivere che x =(5 +/- 11)/6.

7. Risolvi i numeri positivi e negativi. Una volta eliminata la radice quadrata, puoi continuare fino a trovare le risposte negative e positive per x. Ora che hai (5 +/- 11)/6, puoi annotare le due possibilità:

8. Risolvi le risposte positive e negative. Calcola ulteriormente:

9. Semplificare. Per semplificare, dividi le risposte per il numero più grande divisibile sia per il numeratore che per il denominatore. Quindi dividi la prima frazione per 2 e la seconda per 6 e hai risolto x.
Metodo 3 di 3: dividere il quadrato

1. Sposta tutti i termini su un lato dell`equazione. Assicurati che il un di x è positivo. Ecco come farlo:
- 2x - 9 = 12x =
- 2x - 12x - 9 = 0
- In questa equazione, un uguale a 2, B è -12, e C è -9.

2. Sposta la costante C dall`altra parte. La costante è il valore numerico senza una variabile. Spostalo sul lato destro dell`equazione:

3. Dividi i due lati per il coefficiente di un o x termine. Se x non ha un termine davanti e ha un coefficiente con valore 1, puoi saltare questo passaggio. In questo caso, devi dividere tutti i termini per 2, in questo modo:

4. Parte B per due, quadralo e aggiungi i risultati su entrambi i lati del segno is.IlB in questo esempio è -6. Ecco come farlo:

5. Semplifica entrambe le parti. Calcola i termini a sinistra per ottenere (x-3)(x-3) o (x-3). Aggiungi i termini a destra per ottenere 9/2 + 9 o 9/2 + 18/2, che si sommano a 27/2.

6. Trova la radice quadrata di entrambi i lati. La radice quadrata di (x-3) è semplicemente (x-3). Puoi anche scrivere la radice quadrata di 27/2 come ±√(27/2). Pertanto, x - 3 = ±√(27/2).

7. Semplifica la radice quadrata e risolvi per x. Per semplificare ±√(27/2), cerca un quadrato o un numero quadrato perfetto con i numeri 27 o 2 o nei loro fattori. Il numero quadrato 9 si trova in 27, perché 9 x 3 = 27. Per eliminare 9 dalla radice, scrivilo come radice separata e semplifica a 3, la radice quadrata di 9. Lascia √3 al numeratore della frazione perché non può essere separato come fattore da 27 e fai 2 il denominatore. Quindi sposta la costante 3 dal lato sinistro dell`equazione al lato destro e scrivi le tue due soluzioni per x:
Consigli
- Come puoi vedere, il segno radicale non è del tutto scomparso. Pertanto i termini nel numeratore non vengono fusi (non sono termini uguali). Quindi è inutile dividere gli svantaggi e i vantaggi. Invece, dividendo, ci assicuriamo che ogni fattore comune scompaia – ma "SOLO" se il fattore è uguale per entrambe le costanti, "E" il coefficiente della radice quadrata.
Articoli sull'argomento "Risolvi equazioni quadratiche"
Condividi sui social network:
Popolare