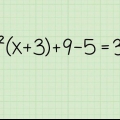Ricorda la regola d`oro dell`algebra. Quello che fai da un lato dell`equazione, devi farlo dall`altro lato, per renderlo giusto. Quindi anche 7 è stato sottratto da 15. Il 7 deve essere sottratto solo una volta per lato. Pertanto non viene sottratto da -4x. 
-4x + 7 = 15 = -4x = 8 
Ancora una volta, quello che fai da un lato dell`equazione lo devi fare dall`altro.Ecco perché dice due volte ÷ -4. 


Sommando +3 al lato sinistro dell`equazione, -2x -3, si ottiene (-2x -3) + 3 o -2x a sinistra. Sommando +3 al lato destro dell`equazione, 4x -15, si ottiene (4x - 15) +3 o 4x -12. Quindi, (-2x - 3) +3 = (4x - 15) +3 = -2x = 4x - 12 La nuova equazione è -2x = 4x -12 
-2x - 4x = (4x - 12) - 4x = -6x = -12 
-6x -6 = -12 ÷ -6 x = 2 

x/5 + 7 = -3 = (x/5 + 7) - 7 = -3 - 7 = x/5 = -10 x/5 * 5 = -10 * 5 x = -50
Risolvi un'equazione in due passaggi
Contenuto
Le equazioni che puoi risolvere in due passaggi sono relativamente facili, dopotutto bastano solo due passaggi. Per risolvere un`equazione del genere tutto ciò che devi fare è isolare la variabile aggiungendo, sottraendo, moltiplicando o dividendo. Se vuoi sapere come e in che modo risolvere le equazioni in due passaggi, segui le istruzioni seguenti.
Passi
Metodo 1 di 3: Risolvere equazioni con una variabile

1. Scrivi il problema. Il primo passo per risolvere un`equazione del genere è scriverla in modo da poter avere una visione d`insieme migliore del problema. Supponiamo di avere il seguente problema: -4x + 7 = 15.

2. Decidi se utilizzare l`addizione o la sottrazione per isolare il termine richiesto. Il prossimo passo è trovare un modo per lasciare -4x su un lato e le costanti (interi) sull`altro lato. Per fare ciò devi trovare l`opposto di +7, che è -7. Sottrarre 7 da entrambi i lati dell`equazione per eliminare il +7 che si trova sullo stesso lato della variabile. Basta scrivere -7 sotto 7 da un lato e sotto 15 dall`altro in modo che l`equazione sia corretta su entrambi i lati.

3. Aumenta o diminuisci l`equazione su entrambi i lati. Dopo questo, la variabile è isolata. Sottraendo 7 dal lato sinistro dell`equazione, questo lato diventa 0, lasciando 8 sul lato destro dell`equazione. Quindi la nuova equazione diventa -4x = 8.

4. Rimuovere il coefficiente della variabile moltiplicando o dividendo. Il coefficiente è il numero associato alla variabile. In questo esempio, il coefficiente è -4. Per rimuovere -4 da -4x, dividi entrambi i lati dell`equazione per -4.

5. Risolvi per la variabile. Per fare ciò, dividi il lato sinistro dell`equazione per -4 per ottenere x. Dividi il lato destro dell`equazione per -4 per ottenere -2.Quindi, x = -2. Ora hai risolto l`equazione in due passaggi: sottrazione e divisione.
Metodo 2 di 3: Risolvi equazioni con una variabile su ciascun lato

1. Scrivi il compito. Il problema su cui lavorerai è il seguente: -2x - 3 = 4x - 15. Prima di continuare: assicurati che entrambe le variabili siano uguali tra loro. In questo caso, -2x e 4x hanno entrambi la stessa variabile x, quindi puoi continuare.

2. Porta entrambe le costanti sul lato destro dell`equazione. Per fare ciò è necessario aggiungere o sottrarre in modo da poter rimuovere la costante sul lato sinistro dell`equazione. La costante è -3, quindi è necessario utilizzare l`opposto, +3, e aggiungere questa costante a entrambi i lati dell`equazione.

3. Sposta le variabili sul lato sinistro dell`equazione. Per fare ciò devi solo sottrarre -4x da entrambi i lati dell`equazione. A sinistra, -2x - 4x = -6x, ea destra, (4x -12) -4x = -12. Questo rende la nuova equazione: -6x = -12

4. Risolvi per la variabile. Ora che hai semplificato l`equazione in -6x = -12, tutto ciò che devi fare è dividere entrambi i lati dell`equazione per -6 per isolare la variabile x, che viene moltiplicata per -6. Sul lato sinistro dell`equazione, -6x ÷ -6 = xe sul lato destro, -12 ÷ -6 = 2. quindi x = 2.
Metodo 3 di 3: Altri modi per risolvere un`equazione in due fasi

1. Risolvi le equazioni in due passaggi mantenendo la variabile sul lato destro dell`equazione.Finché isoli la variabile ottieni la stessa risposta. Diamo un`occhiata al prossimo problema, 11 = 3 - 7x.Per risolvere questo problema, il primo passo è combinare il denaro sottraendo 3 da entrambi i lati dell`equazione. Quindi devi dividere entrambi i membri per -7 per risolvere x. Di seguito puoi vedere come va:
- 11 = 3 - 7x =
- 11 - 3 = 3 - 3 - 7x =
- 8 = - 7x =
- 8/-7 = -7/7x
- -8/7 = x o -1.14 = x

2. Risolvi un`equazione in due passaggi moltiplicando invece di dividere alla fine. Il principio per risolvere questo tipo di equazioni è lo stesso: combinare le costanti tra loro e quindi isolare la variabile senza un termine. Prendiamo come esempio il seguente problema, x/5 + 7 = -3. La prima cosa da fare è sottrarre 7 da entrambi i membri dell`equazione, quindi moltiplicare entrambi i membri per 5 per risolvere x. Ecco come puoi farlo:
Consigli
- Se non c`è un numero davanti a x, supponiamo che sia 1x.
- Potrebbe non esserci una costante su entrambi i lati dell`equazione. Se non c`è un numero dopo x, supponiamo che valga quanto segue: `x + 0`.
Articoli sull'argomento "Risolvi un'equazione in due passaggi"
Condividi sui social network:
Popolare