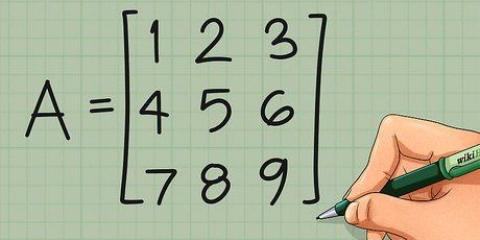Se hai più variabili, continua la riga per tutto il tempo necessario. Ad esempio, se stavi cercando di risolvere un sistema di sei variabili, la tua forma standard sarebbe Au+Bv+Cw+Dx+Ey+Fz=G. In questo articolo ci concentreremo sui sistemi con solo tre variabili. Risolvere un sistema più grande è esattamente lo stesso, ma richiede solo più tempo e più passaggi. Si noti che in forma standard le operazioni tra i termini sono sempre un`aggiunta. Se c`è una sottrazione nella tua equazione, invece di un`addizione, dovrai lavorarci in seguito rendendo il tuo coefficiente negativo. Per renderlo più facile da ricordare, puoi riscrivere l`equazione e aggiungere l`operazione e rendere negativo il coefficiente. Ad esempio, puoi riscrivere l`equazione 3x-2y+4z=1 come 3x+(-2y)+4z=1. 
Supponiamo di avere un sistema costituito dalle tre equazioni 3x+y-z=9, 2x-2y+z=-3 e x+y+z=7. La riga superiore della matrice conterrà i numeri 3, 1, -1, 9, poiché questi sono i coefficienti e la soluzione della prima equazione. Si noti che qualsiasi variabile che non ha un coefficiente si presume abbia un coefficiente di 1. La seconda riga della matrice diventa 2, -2, 1, -3 e la terza riga 1, 1, 1, 7. Assicurati di allineare i coefficienti x nella prima colonna, i coefficienti y nella seconda, i coefficienti z nella terza e i termini di soluzione nella quarta. Quando hai finito di lavorare con la matrice, queste colonne saranno importanti quando scrivi la tua soluzione. 

Puoi indicare qualsiasi posizione specifica in una matrice usando una combinazione di R e C. Ad esempio, per denotare un termine nella seconda riga, terza colonna, potresti chiamarlo R2C3. 

È comune utilizzare le frazioni nella moltiplicazione scalare perché spesso si desidera ottenere una riga diagonale di 1. Abituati a lavorare con le frazioni. Sarà anche più facile (per la maggior parte dei passaggi nella risoluzione della matrice) essere in grado di scrivere le tue frazioni in forma impropria, quindi riconvertirle in numeri misti per la soluzione finale. Ecco perché è più facile lavorare con il numero 1 2/3 se lo scrivi come 5/3. Ad esempio, la prima riga (R1) del nostro problema di esempio inizia con i termini [3.1,-1,9]. La matrice della soluzione deve contenere un 1 nella prima posizione della prima riga. Per "trasformare" il 3 in un 1, possiamo moltiplicare l`intera riga per 1/3. Questo crea il nuovo R1 di [1.1/3,-1/3.3]. Assicurati di lasciare tutti i segni negativi a cui appartengono. 
È possibile utilizzare la notazione abbreviata e dichiarare questa operazione come R2-R1=[0,-1,2,6]. Ricorda che addizione e sottrazione sono solo forme opposte della stessa operazione. Puoi pensarlo come sommare due numeri o sottrarre il contrario. Ad esempio, se inizi con la semplice equazione 3-3=0, puoi pensare a questo come un problema di addizione di 3+(-3)=0. Il risultato è lo stesso. Sembra semplice, ma a volte è più facile considerare un problema in una forma o nell`altra. Tieni d`occhio i tuoi segni negativi. 
Coppia; che esiste una riga 1 di [1,1,2,6] e una riga 2 di [2,3,1,1]. Vuoi un termine 0 nella prima colonna di R2. Cioè, vuoi cambiare il 2 in uno 0. Per farlo devi sottrarre un 2. Puoi ottenere un 2 moltiplicando prima la riga 1 per la moltiplicazione scalare 2, quindi sottraendo la prima riga dalla seconda riga. In forma abbreviata può essere scritto come R2-2*R1. Per prima cosa moltiplica R1 per 2 per ottenere [2,2,4,12]. Quindi sottrai questo da R2 per ottenere [(2-2),(3-2),(1-4),(1-12)]. Semplifica questo e il tuo nuovo R2 diventa [0,1,-3,-11]. 
Un errore comune si verifica quando si esegue una moltiplicazione e un`addizione combinate in una mossa. Ad esempio, supponiamo di dover sottrarre due volte R1 da R2. Quando moltiplichi R1 per 2 per fare questo passaggio, ricorda che R1 non cambia nella matrice. Fai solo la moltiplicazione per cambiare R2. Copia prima R1 nella sua forma originale, quindi apporta la modifica a R2. 
1. Fai un 1 nella prima riga, prima colonna (R1C1). 2. Fai uno 0 nella seconda riga, prima colonna (R2C1). 3. Fai un 1 nella seconda riga, seconda colonna (R2C2). 4. Fai uno 0 nella terza riga, prima colonna (R3C1). 5. Fai uno 0 nella terza riga, seconda colonna (R3C2). 6. Fai un 1 nella terza riga, terza colonna (R3C3). 
Crea uno 0 nella seconda riga, terza colonna (R2C3). Crea uno 0 nella prima riga, terza colonna (R1C3). Crea uno 0 nella prima riga, seconda colonna (R1C2). 


Nota che la moltiplicazione e la divisione sono solo funzioni inverse l`una dell`altra. Possiamo dire che moltiplichiamo per 1/3 o dividiamo per 3, senza cambiare il risultato. 
Scrivi la riga 3 (che non è cambiata) se R3=[1,1,1,7]. Fai attenzione quando sottrai numeri negativi per assicurarti che i caratteri rimangano corretti. Ora prima mettiamo le frazioni nella loro forma impropria. Ciò semplifica i passaggi successivi della soluzione. È possibile semplificare le frazioni nell`ultimo passaggio del problema. 
Nota che se la metà sinistra della sequenza inizia ad assomigliare alla soluzione con 0 e 1, la metà destra può sembrare brutta, con frazioni improprie. Lasciali per quello che sono ora. Non dimenticare di continuare a copiare le righe non interessate, quindi R1=[1,1/3,-1/3,3] e R3=[1,1,1,7]. 
Continua a copiare lungo R1=[1.1/3,-1/3.3] e R2=[0.1,-5/8.27/8]. Ricorda che cambi solo una riga alla volta. 

Nota che le frazioni che sembravano piuttosto complicate nel passaggio precedente stanno già iniziando a risolversi. Continuare con R1=[1.1/3,-1/3.3] e R2=[0.1,-5/8.27/8]. Nota che a questo punto hai la diagonale di 1 per la matrice della soluzione. Hai solo bisogno di convertire tre elementi della matrice in 0 per trovare la tua soluzione. 
Quindi prendi R1=[1,1/3,-1/3,3] e R3=[0,0,1,1]. 
Prendi R2=[0,1,0,4] e R3=[0,0,1,1] invariati. 

1002 0104 0011 


Poiché ogni equazione si semplifica in una vera affermazione matematica, le tue soluzioni sono corrette. Se una delle soluzioni non è corretta, controlla di nuovo il tuo lavoro e cerca eventuali errori. Alcuni errori comuni si verificano quando si eliminano i segni meno lungo il percorso o quando si confonde la moltiplicazione e l`addizione di frazioni. 
Risolvi matrici
Contenuto
Una matrice è un modo molto utile per rappresentare i numeri in un formato a blocchi, che puoi quindi utilizzare per risolvere un sistema di equazioni lineari. Se hai solo due variabili, probabilmente utilizzerai un metodo diverso. Leggi questo in Risolvere un sistema di equazioni per esempi di questi altri metodi. Ma se hai tre o più variabili, una matrice è l`ideale. Usando ripetute combinazioni di moltiplicazione e addizione, puoi arrivare sistematicamente a una soluzione.
Passi
Parte 1 di 4: Elaborazione della matrice

1. Verifica di disporre di dati sufficienti. Per ottenere una soluzione unica per ogni variabile in un sistema lineare usando una matrice, devi avere tante equazioni quante sono le variabili che stai cercando di risolvere. Ad esempio: con le variabili x, yez sono necessarie tre equazioni. Se hai quattro variabili, hai bisogno di quattro equazioni.
- Se hai meno equazioni del numero di variabili, imparerai alcuni limiti delle variabili (come x = 3y e y = 2z), ma non sarai in grado di ottenere una soluzione precisa. Per questo articolo lavoreremo solo verso una soluzione unica.

2. Scrivi le tue equazioni in forma standard. Prima di poter trasferire i dati dalle equazioni in una forma matriciale, devi prima scrivere ciascuna equazione in forma standard. La forma standard per un`equazione lineare è Ax+By+Cz=D, dove le lettere maiuscole sono i coefficienti (numeri) e l`ultimo numero (in questo esempio, la D) è a destra del segno di uguale.

3. Metti i numeri del sistema di equazioni in una matrice. Una matrice è un gruppo di numeri, disposti in una specie di tabella, con cui lavoreremo per risolvere il sistema. Fondamentalmente contiene gli stessi dati delle equazioni stesse, ma in un formato più semplice. Per creare la matrice delle tue equazioni in forma standard, copia semplicemente i coefficienti e il risultato di ciascuna equazione in una singola riga e impila quelle righe una sopra l`altra.

4. Disegna una grande parentesi quadra attorno all`intera matrice. Per convenzione, una matrice è indicata da una coppia di parentesi quadre, [ ], attorno all`intero blocco di numeri. Le parentesi non influiscono in alcun modo sulla soluzione, ma indicano che stai lavorando con le matrici. Una matrice può essere composta da un numero qualsiasi di righe e colonne. In questo articolo useremo le parentesi attorno a una riga di termini per indicare che appartengono insieme.

5. Uso del simbolismo comune. Quando si lavora con le matrici è comune fare riferimento alle righe con la sigla R e alle colonne con la sigla C. Puoi utilizzare i numeri insieme a queste lettere per designare una riga o una colonna specifica. Ad esempio, per indicare la riga 1 di una matrice, puoi scrivere R1. La riga 2 diventa quindi R2.
Parte 2 di 4: Apprendimento delle operazioni per risolvere un sistema con una matrice

1. Comprendere la forma della matrice della soluzione. Prima di iniziare a risolvere il tuo sistema di equazioni, devi capire cosa farai con la matrice. A questo punto hai una matrice che assomiglia a questa:
- 31-19
- 2-21-3
- 1117
- Lavori con una serie di operazioni di base per creare la "matrice della soluzione". La matrice della soluzione sarà simile a questa:
- 100 volte
- 010 anni
- 001z
- Nota che la matrice è composta da 1 in una linea diagonale con 0 in tutti gli altri spazi tranne la quarta colonna. I numeri nella quarta colonna sono le soluzioni per le variabili x, yez.

2. Usa la moltiplicazione scalare. Il primo strumento a tua disposizione per risolvere un sistema utilizzando una matrice è la moltiplicazione scalare. Questo è semplicemente un termine che significa che moltiplichi gli elementi in una riga della matrice per un numero costante (non una variabile). Quando usi la moltiplicazione scalare, tieni presente che devi moltiplicare ogni termine dell`intera sequenza per il numero che selezioni. Se dimentichi il primo termine e moltiplichi, otterrai una soluzione sbagliata. Tuttavia, non è necessario moltiplicare l`intera matrice contemporaneamente. Con la moltiplicazione scalare lavori solo su una riga alla volta.

3. Usa l`addizione di riga o la sottrazione di riga. Il secondo strumento che puoi utilizzare è aggiungere o sottrarre due righe della matrice. Per creare i termini 0 nella matrice della soluzione, devi aggiungere o sottrarre numeri per arrivare allo 0. Ad esempio, se R1 di una matrice è [1,4,3,2] e R2 è [1,3,5,8], puoi sottrarre la prima riga dalla seconda riga e creare una nuova riga [ 0,-1, 2,6], perché 1-1=0 (prima colonna), 3-4=-1 (seconda colonna), 5-3=2 (terza colonna) e 8-2=6 (quarta colonna). Quando esegui un`addizione o una sottrazione di righe, riscrivi il tuo nuovo risultato invece della riga con cui hai iniziato. In questo caso estraiamo la riga 2 e inseriamo la nuova riga [0,-1,2,6].

4. Combina l`addizione di righe e la moltiplicazione scalare in un unico passaggio. Non puoi aspettarti che i termini corrispondano sempre, quindi puoi usare una semplice addizione o sottrazione per creare 0 nella tua matrice. Più spesso dovrai aggiungere (o sottrarre) un multiplo di un`altra riga. Per fare ciò, esegui prima la moltiplicazione scalare, quindi aggiungi quel risultato alla riga di destinazione che stai cercando di modificare.

5. Copia le righe che rimangono invariate mentre lavori. Mentre lavori sulla matrice, cambierai una singola riga alla volta, mediante moltiplicazione scalare, addizione di riga o sottrazione di riga, oppure mediante una combinazione di passaggi. Quando modifichi una riga, assicurati di copiare le altre righe della matrice nella loro forma originale.

6. Lavora prima dall`alto verso il basso. Per risolvere il sistema, lavori secondo uno schema molto organizzato, essenzialmente "risolvendo" un termine della matrice alla volta. L`ordine per un array a tre variabili sarà simile a questo:

7. Ritorna dal basso verso l`alto. A questo punto, se hai eseguito correttamente i passaggi, sei a metà della soluzione. Devi avere la linea diagonale di 1, con 0 sotto di essa. I numeri nella quarta colonna non contano a questo punto. Ora esegui il backup come segue:

8. Verifica di aver creato la matrice della soluzione. Se il tuo lavoro è corretto, hai creato la matrice della soluzione con 1 in una linea diagonale di R1C1, R2C2, R3C3 e 0 nelle altre posizioni delle prime tre colonne. I numeri nella quarta colonna sono le soluzioni per il tuo sistema lineare.
Parte 3 di 4: Mettere insieme i passaggi per risolvere il sistema

1. Inizia con un esempio di sistema di equazioni lineari. Per esercitarti con questi passaggi, iniziamo con il sistema che abbiamo usato in precedenza: 3x+y-z=9, 2x-2y+z=-3 e x+y+z=7. Se lo scrivi in una matrice, hai R1= [3.1,-1,9], R2=[2,-2,1,-3] e R3=[1,1,1,7].

2. Creare un 1 nella prima posizione R1C1. Si noti che attualmente R1 inizia con un 3. Devi cambiarlo in 1. Puoi farlo moltiplicando scalare, moltiplicando tutti e quattro i termini di R1 per 1/3. In stenografia puoi scrivere come R1*1/3. Questo dà un nuovo risultato per R1 se R1=[1,1/3,-1/3,3]. Adottare R2 e R2, invariati, se R2=[2,-2,1,-3] e R3=[1,1,1,7].

3. Crea uno 0 nella seconda riga, prima colonna (R2C1). A questo punto R2=[2,-2,1,-3]. Per avvicinarsi alla matrice della soluzione, è necessario modificare il primo termine da 2 a 0. Puoi farlo sottraendo il doppio del valore da R1, poiché R1 inizia con un 1. In breve l`operazione è R2-2*R1. Ricorda che non cambi R1, lavora solo con esso. Quindi prima copia R1 se R1=[1,1/3,-1/3,3]. Se poi raddoppi ogni termine di R1, ottieni 2*R1=[2,2/3,-2/3,6]. Infine, sottrai questo risultato dall`originale R2 per ottenere il tuo nuovo R2. Lavorando termine per termine, questa sottrazione diventa (2-2), (-2-2/3), (1-(-2/3), (-3-6). Semplifichiamo questo con il nuovo R2=[0,-8/3,5/3,-9]. Nota che il primo termine è 0 (qualunque fosse il tuo obiettivo).

4. Crea un 1 nella seconda riga, seconda colonna (R2C2). Per continuare a formare la linea diagonale degli 1, devi convertire il secondo termine -8/3 in 1. Fallo moltiplicando l`intera riga per il reciproco di quel numero (-3/8). Simbolicamente, questo passaggio è R2*(-3/8). La seconda riga risultante è R2=[0.1,-5/8.27/8].

5. Crea uno 0 nella terza riga, prima colonna (R3C1). Il tuo focus ora si sposta sulla terza riga, R3=[1,1,1,7]. Per fare uno 0 nella prima posizione, devi sottrarre un 1 dall`1 attualmente in quella posizione. Se guardi in alto, c`è un 1 nella prima posizione di R1. Quindi devi solo sottrarre R1 da R3 per ottenere il risultato di cui hai bisogno. Termine per termine diventa (1-1), (1-1/3), (1-(-1/3)), (7-3). Questi quattro mini-problemi possono quindi essere semplificati nel nuovo R3=[0.2/3.4/3.4].

6. Fai uno 0 nella terza riga, seconda colonna (R3C2). Questo valore è attualmente 2/3, ma deve essere convertito in 0. A prima vista, sembra che tu possa sottrarre due volte i valori di R1, poiché la colonna corrispondente di R1 contiene un 1/3. Tuttavia, se raddoppi e sottrai tutti i valori di R1, lo 0 nella prima colonna di R3 cambia, cosa che non vuoi. Questo sarebbe un passo indietro nella tua soluzione. Quindi devi lavorare con una combinazione di R2. Se sottrai 2/3 da R2, crei uno 0 nella seconda colonna, senza cambiare la prima colonna. In forma abbreviata è R3- 2/3*R2. I singoli termini diventano (0-0), (2/3-2/3), (4/3-(-5/3*2/3)), (4-27/8*2/3). La semplificazione fornisce quindi R3=[0,0,42/24.42/24].

7. Crea un 1 nella terza riga, terza colonna (R3C3). Questa è una semplice moltiplicazione con il reciproco del numero che dice. Il valore corrente è 42/24, quindi puoi moltiplicare per 24/42 per ottenere il valore desiderato di 1. Nota che i primi due termini sono entrambi 0, quindi qualsiasi moltiplicazione rimane 0. Il nuovo valore di R3=[0,0,1,1].

8. Crea uno 0 nella seconda riga, terza colonna. R2 è attualmente [0.1,-5/8.27/8], con un valore di -5/8 nella terza colonna. Devi trasformarlo in uno 0. Ciò significa che devi eseguire qualche operazione con R3 che consiste nell`aggiungere 5/8. Poiché la terza colonna corrispondente di R3 è un 1, è necessario moltiplicare tutti i valori di R3 per 5/8 e aggiungere il risultato a R2. In breve questo è R2+5/8*R3. Termine per termine questo è R2=(0+0), (1+0), (-5/8+5/8), (27/8+5/8). Questo può essere semplificato in R2=[0,1,0,4].

9. Crea uno 0 nella prima riga, terza colonna (R1C3). La prima riga è attualmente R1=[1.1/3,-1/3.3]. Devi convertire il -1/3 nella terza colonna in uno 0, usando una combinazione di R3. Non vuoi usare R2, perché l`1 nella seconda colonna di R2, modificherebbe R1 nel modo sbagliato. Quindi moltiplichi R3*1/3 e aggiungi il risultato a R1. La notazione per questo è R1+1/3*R3. L`elaborazione termine per termine risulta in R1=(1+0), (1/3+0), (-1/3+1/3), (3+1/3). Puoi semplificarlo in un nuovo R1=[1,1/3,0,10/3].

10. Fai uno 0 nella prima riga, seconda colonna (R1C2). Se tutto è fatto bene, questo dovrebbe essere l`ultimo passaggio. Devi convertire 1/3 nella seconda colonna in 0. Puoi ottenerlo moltiplicando e sottraendo R2*1/3. In breve questo è R1-1/3*R2. Il risultato è R1=(1-0), (1/3-1/3), (0-0), (10/3-4/3). Semplificando poi si ottiene R1=[1,0,0,2].

11. Cerca la matrice della soluzione. A questo punto, se tutto è andato bene, avresti le tre righe R1=[1,0,0,2], R2=[0,1,0,4] e R3=[0,0,1,1] dover avere. Nota che se lo scrivi in forma di matrice a blocchi con le righe una sopra l`altra, hai 1 diagonali con 0 più avanti e le tue soluzioni sono nella quarta colonna. La matrice della soluzione dovrebbe assomigliare a questa:

12. Capire la tua soluzione. Dopo aver convertito le equazioni lineari in una matrice, metti i coefficienti x nella prima colonna, i coefficienti y nella seconda colonna, i coefficienti z nella terza colonna. Se ora vuoi riscrivere la matrice in equazioni, queste tre linee della matrice in realtà significano le tre equazioni 1x+0y+0z=2, 0x+1y+0z=4 e 0x+0y+1z=1. Poiché possiamo cancellare gli 0 termini e non dover scrivere i coefficienti 1, queste tre equazioni si semplificano alla soluzione, x=2, y=4 e z=1. Questa è la soluzione al tuo sistema di equazioni lineari.
Parte 4 di 4: Verifica della tua soluzione

1. Elabora le soluzioni in ogni variabile in ogni equazione. È sempre una buona idea verificare se la tua soluzione è effettivamente corretta. Lo fai testando i tuoi risultati nelle equazioni originali.
- Le equazioni originali per questo problema erano: 3x+y-z=9, 2x-2y+z=-3 e x+y+z=7. Quando sostituisci le variabili con i loro valori che hai trovato, ottieni 3*2+4-1=9, 2*2-2*4+1=-3 e 2+4+1=7.

2. Semplifica qualsiasi equazione. Eseguire le operazioni in ciascuna equazione secondo le regole di base delle operazioni. La prima equazione si semplifica in 6+4-1=9 o 9=9. La seconda equazione può essere semplificata in 4-8+1=-3 o -3=-3. L`ultima equazione è semplicemente 7=7.

3. Scrivi le tue soluzioni finali. Per questo dato problema la soluzione finale è x=2, y=4 e z=1.
Consigli
- Se il tuo sistema di equazioni è molto complesso, con molte variabili, potresti voler usare una calcolatrice grafica invece di fare il lavoro a mano. Per informazioni a riguardo puoi anche consultare wikiHow.
Articoli sull'argomento "Risolvi matrici"
Condividi sui social network:
Popolare