Trasporre una Matrice: 11 Passaggi (con Immagini)

Contenuto

Passi
Consigli

Una trasposizione di matrici è un utile strumento matematico per comprendere la struttura delle matrici. Funzioni che potresti già conoscere dalle matrici, come il quadrato e la simmetria, influenzano i risultati della trasposizione in modo ovvio. La trasposizione serve anche per esprimere i vettori come matrici o per calcolare i prodotti dei vettori. Quando si tratta di matrici complesse, il concetto strettamente correlato di una trasposizione coniugata ti aiuterà con molti problemi.

Passi

Parte 1 di 3: Trasporre una matrice

Immagine titolata Transpose a Matrix Step 1

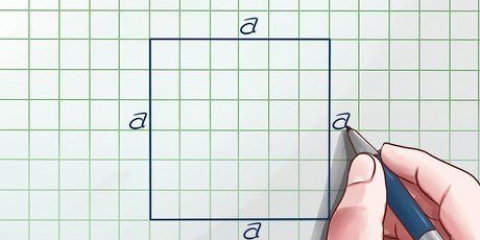
1. Inizia con qualsiasi matrice. Puoi trasporre qualsiasi matrice indipendentemente dal numero di righe e colonne. Le matrici quadrate, con un numero uguale di righe e colonne, sono le più trasposte, quindi useremo una semplice matrice quadrata come esempio:

matrice un =
1 2 3
4 5 6
7 8 9

Immagine titolata Transpose a Matrix Step 2

2. Rendi la prima riga della matrice la prima colonna della trasposizione. Riscrivi la prima riga della matrice come una colonna:

Trasposizione della matrice A = A

Prima colonna di A:
1
2
3

Immagine titolata Transpose a Matrix Step 3

3. Ripetere per le righe rimanenti. La seconda riga della matrice originale diventa la seconda colonna della trasposizione. Ripeti questo schema finché non hai trasformato ogni riga in una colonna:

un =
1 4 7
2 5 8
3 6 9

Immagine titolata Transpose a Matrix Step 4

4. Esercitati su una matrice non quadrata. La trasposizione è esattamente la stessa per una matrice non quadrata. Riscrivi la prima riga come prima colonna, la seconda riga come seconda colonna e così via. Ecco un esempio con codice colore per mostrarti dove finiscono gli elementi:

matrice z =
4 7 2 1
3 9 8 6

matrice z =
4 3
7 9
2 8
1 6

Immagine titolata Transpose a Matrix Step 5

5. Esprimi matematicamente la trasposizione. Il concetto è abbastanza semplice, ma è bene poterlo descrivere in termini matematici. Non è necessario alcun gergo al di fuori della notazione di base della matrice:

Se la matrice B è a m X n matrice (m righe e n colonne), allora la matrice trasposta B è a n X m matrice (n righe e m colonne).

Per ogni elemento b_xy (X-il, y-la colonna) in B, la matrice B ha un elemento uguale su b_yx (y-la riga, X-la colonna).

Parte 2 di 3: Casi speciali

Immagine titolata Transpose a Matrix Step 6

1. (M = M. La trasposizione di una trasposizione è la matrice originale. Questo ha molto senso, dal momento che stai solo scambiando righe e colonne. Scambiarli di nuovo ti riporterà all`inizio.

Immagine titolata Transpose a Matrix Step 7

2. Inclinare le matrici quadrate sulla diagonale principale. In una matrice quadrata, una trasposizione "inclinerà" la matrice lungo la diagonale principale. In altre parole, gli elementi in una linea diagonale dell`elemento a₁₁ nell`angolo in basso a destra rimangono gli stessi. Gli altri elementi si sposteranno lungo la diagonale e finiranno alla stessa distanza dalla diagonale, sul lato opposto.

Se non riesci a visualizzarlo, disegna una matrice 4x4 su un pezzo di carta. Ora piega la diagonale principale. Vedi come gli elementi a₁₄ e un₄₁ toccarsi? Si scambiano di posto nella trasposizione, proprio come qualsiasi altra coppia che si tocca una volta piegata.

Immagine titolata Transpose a Matrix Step 8

3. Trasporre una matrice simmetrica. Una matrice simmetrica è simmetrica rispetto alla diagonale principale. Se utilizziamo il `tilt` o `fold` come descritto sopra, possiamo immediatamente vedere che non cambia nulla. Tutte le coppie di elementi che si scambiano di posto erano già identiche. In effetti, questo è il modo standard per definire una matrice simmetrica. Se la matrice A = A, allora la matrice A è simmetrica.

Parte 3 di 3: Trasposizione coniugata di una matrice complessa

Immagine titolata Transpose a Matrix Step 9

1. Inizia con una matrice complessa. Le matrici complesse hanno elementi con una componente reale e una immaginaria. Sebbene tu possa eseguire una trasposizione regolare di queste matrici, la maggior parte dei calcoli pratici sono invece trasposizioni coniugate.

Matrice C =
2+io 3-2io
0+io 5+0io

Immagine titolata Transpose a Matrix Step 10

2. Prendi la coniugazione complessa. La complessa coniugazione cambia il segno delle componenti immaginarie, senza cambiare le componenti reali. Eseguire questa operazione per tutti gli elementi della matrice.

Coniugazione complessa di C =
2-io 3+2io
0-io 5-0io

Immagine titolata Transpose a Matrix Step 11

3. Trasponi i risultati. Prendi una normale conversione del risultato. La matrice che ottieni è la trasposizione coniugata della matrice originale.

Trasposizione coniugata di C = C =
2-io 0-io
3+2io 5-0io

Consigli

Questo articolo usa la notazione A per denotare la conversione della matrice A. La notazione A` o Ã significa lo stesso.
Questo articolo si riferisce alla conversione coniugata della matrice A in A, la notazione più comune nell`algebra lineare. I fisici quantistici usano spesso invece A. A* è un`altra opzione, ma cerca di evitarlo poiché alcune fonti utilizzeranno questo simbolo per indicare una coniugazione complessa.