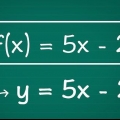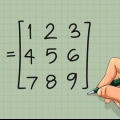Trovare l'Inverso di una Matrice 3x3: 6 Passaggi (con Immagini)

Contenuto

Passi
Consigli
Avvertenze

Calcolare a mano l`inverso di una matrice 3x3 è un compito noioso. Ma è anche utile e non difficile e aiuta a risolvere varie equazioni di matrici.

Passi

1. Determina det(M), il determinante della Matrice M. Il determinante è solitamente al denominatore dell`inverso. Se il determinante è uguale a zero, la matrice non ha inversa.

2. Determina M, la trasposizione della matrice. Trasporre significa rispecchiare la matrice nella diagonale principale o qualunque sia la stessa, scambiando l`elemento (i,j) e l`elemento (j,i).

3. Determina il determinante di ciascuna delle matrici minori 2x2, le minori.

4. Visualizzalo come una matrice di cofattori come mostrato e moltiplica ogni termine per il segno indicato.Il risultato di questi passaggi è la matrice aggiunta (a volte anche matrice aggiunta), scritta come Adj(M).

5. Trova l`inversa dividendo la matrice adiuvante trovata nel passaggio precedente per il determinante del primo passaggio.

6. Questi passaggi possono essere combinati trasponendo, copiando le prime due righe e colonne e determinando il determinante 2x2 attorno a ciascun punto. Controllando il lavoro, il determinante viene calcolato in tre modi; se questi corrispondono, allora hai trovato la risposta corretta. Con il "toro" metodo, il segno è immediatamente corretto.

Consigli

Si noti che lo stesso metodo può essere applicato a una matrice di variabili e incognite, ad esempio una matrice algebrica, M, e la sua inversa, M.
Annota tutti i tuoi passaggi perché è molto difficile risolvere a memoria l`inverso di una matrice 3x3. Inoltre, annotare ti assicura di commettere errori meno rapidamente.
Ci sono programmi per computer che calcolano le inverse di una matrice per te. , fino a una dimensione di matrici 30x30

La matrice adiuvata è la trasposizione della matrice dei cofattori. Ecco perché trasponiamo la matrice nel passaggio 2, per trovare una trasposizione di una matrice di cofattori.
Controlla se è corretto moltiplicando M per M. Ora dovresti essere in grado di confermare che M*M = M*M = I. I è la matrice dell`unità, composta da uno lungo la diagonale principale e zeri ovunque. In caso contrario, hai commesso un errore da qualche parte.

Avvertenze

Non tutte le matrici 3x3 hanno un`inversa. Se il determinante della matrice è 0, allora non ha l`inverso. (Nota che nella formula dividiamo per det(M). La divisione per zero non è possibile.)