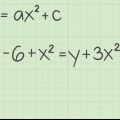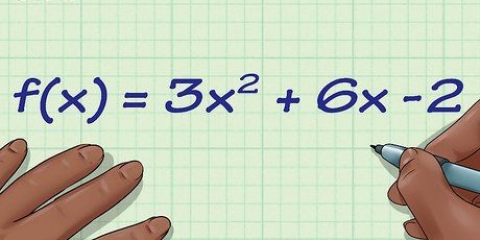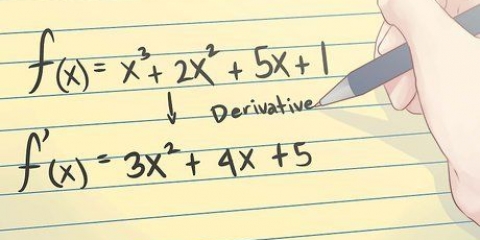Trovare l'Inverso di una Funzione: 5 Passaggi (con Immagini)

Contenuto

Passi
Consigli

Una funzione in matematica (di solito indicata come f(x)) può essere pensata come una specie di formula o programma in cui si inserisce un valore "X" rimbocca, che quindi restituisce un determinato valore per y. Il inverso di una funzione f(x) (indicata come f(x)) è essenzialmente il contrario: immettere a y-valore e ottieni il primo X-valore indietro. Trovare l`inversa di una funzione può sembrare complicato, ma per semplici equazioni, tutto ciò che serve è una certa conoscenza delle operazioni di base in algebra. Leggi le seguenti istruzioni dettagliate e dai un`occhiata all`esempio.

Passi

Immagine titolata Trova algebricamente l`inverso di una funzione Passaggio 01

1. Scrivi la tua funzione, scambiando f(x) con y se necessario. La tua formula appartiene y avere da un lato il segno di uguale e dall`altro il X-termini. Se hai già scritto un`equazione y e X termini (come ad esempio 2 + y = 3x), allora hai solo bisogno y da risolvere isolandolo.

Esempio: abbiamo una funzione f(x) = 5x - 2 e la riscriviamo come y = 5x - 2, semplicemente da "f(x)" essere sostituito da y.
Nota: f(x) è la notazione della funzione standard, ma se hai a che fare con più funzioni, a ciascuna funzione verrà assegnata una lettera iniziale diversa per facilitarne la distinzione. Ad esempio g(x) e h(x) sono lettere comunemente usate per le funzioni.

Immagine titolata Trova algebricamente l`inverso di una funzione Passaggio 02

2. sciolto X in poi. In altre parole, apporta le modifiche necessarie a X isolare su un lato del segno di uguale. Per fare ciò, usa le operazioni di base dell`algebra: if X ha un coefficiente (un numero per la variabile), dividi entrambi i membri dell`equazione per questo numero per annullarlo; c`è una costante all`interno del "X"-termine, quindi calcolalo aggiungendo o sottraendo entrambi i lati del segno di uguale e così via.

Ricorda che ogni operazione su un lato del segno di uguale deve essere eseguita anche sull`altro lato.

Esempio: per continuare con il nostro esempio, aggiungiamo prima 2 su entrambi i lati dell`equazione. Questo ci dà y + 2 = 5x. Quindi dividiamo entrambi i membri dell`equazione per 5, lasciando (y + 2)/5 = x. Infine, per renderlo più leggibile, riscriviamo l`equazione con il "X" A sinistra: x = (y + 2)/5.

Immagine titolata Trova algebricamente l`inverso di una funzione Passaggio 03

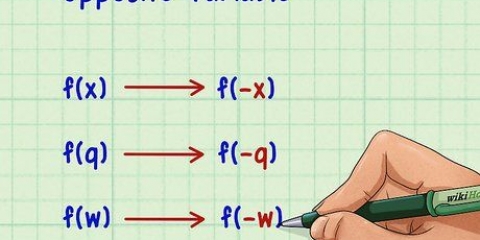
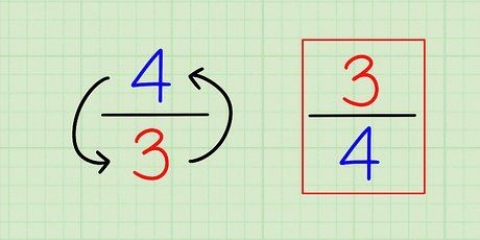
3. Scambia le variabili. Scambio X di y e viceversa. L`equazione risultante è l`inverso della funzione originale. In altre parole, se abbiamo un valore per X compila la nostra equazione originale, quindi possiamo compilare la risposta al contrario (di nuovo per "X") che restituisce il valore originale!

Esempio: dopo aver scambiato x e y, otteniamo y = (x + 2)/5

Immagine titolata Trova algebricamente l`inverso di una funzione Passaggio 04

4. sostituire y per mezzo di "f(x)". Le funzioni inverse sono generalmente indicate come f(x) = (x termini) . Ricordiamo che in questo caso l`esponente -1 non significa che dobbiamo eseguire un`operazione esponenziale sulla funzione. È solo un modo per indicare che questa funzione è l`inverso dell`originale.

Perché X è uguale a 1/x, puoi anche scrivere f(x) come "1/f(x)," un`altra notazione per l`inverso di f(x).

Immagine titolata Trova algebricamente l`inverso di una funzione Passaggio 05

5. Controlla il tuo lavoro. Prova a inserire una costante nella funzione originale per X. Se trovi l`inverso corretto, troverai il valore originale di "X" dovrebbe vederlo di nuovo, se inserisci il risultato di questo al contrario.

Esempio: inseriamo 4 come valore di X nel nostro confronto originale. Questo ci dà f(x) = 5(4) - 2, o f(x) = 18.

Successivamente, inseriremo questo risultato nell`inverso. Quindi sostituiamo 18 nella funzione inversa come valore di X. In questo modo otteniamo y = (18 + 2)/5 come risultato e questo è uguale a y = 4. Quindi 4 è il valore x con cui abbiamo iniziato e con quello sappiamo di aver trovato la giusta funzione inversa.

Consigli

Puoi usare entrambe le notazioni f(x) = y e f^(-1)(x) = y senza problemi se esegui operazioni matematiche sulle funzioni. Ma è meglio tenere separate la funzione originale e la funzione inversa, quindi cerca di mantenerla in notazione comune. Nel caso della funzione inversa la notazione f^(-1)(x).
Si noti che l`inverso di una funzione è solitamente, ma non sempre, una funzione stessa.