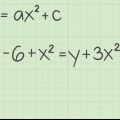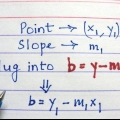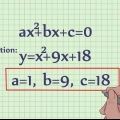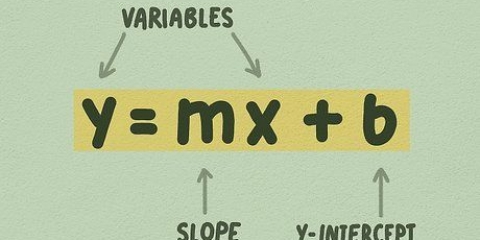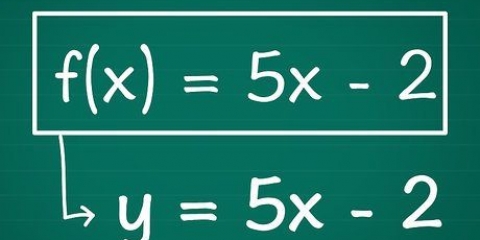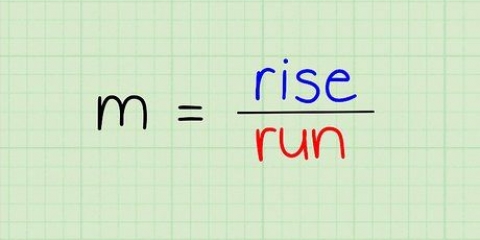Trovare l'Equazione di una Retta Tangente: 4 Passaggi (con Immagini)

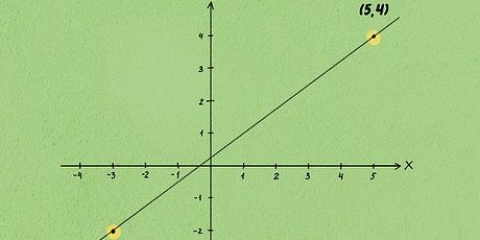
Una tangente a una parabola o curva è una linea che tocca la curva solo in un dato punto. Per trovare l`equazione di questa retta tangente, dovrai calcolare la pendenza della curva in quel punto, il che richiede alcuni calcoli matematici. È quindi possibile scrivere l`equazione della retta tangente in una forma punto-pendenza. Questo articolo spiega i passaggi da eseguire.

Passi

Immagine titolata Trova l`equazione di una retta tangente Step 1

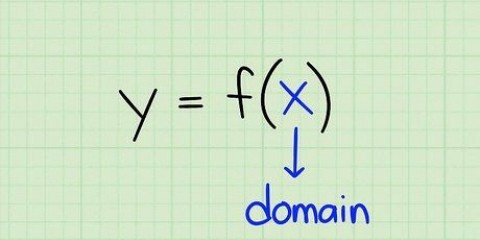
1. L`equazione di una curva può essere espressa come una funzione. Trova la derivata di questa funzione per trovare l`equazione della pendenza di questa curva.

Il modo più semplice per differenziare la maggior parte dei polinomi è attraverso la regola della catena. Moltiplica ogni equazione della funzione per la sua potenza per trovare il coefficiente di quel termine nella derivata, quindi sottrai la potenza per 1.
Esempio: per la funzione f(x) = x^3 + 2x^2 + 5x + 1, la derivata è f`(x) = 3x^2 + 4x + 5.
Per f(x) = (2x+5)^10 + 2*(4x+3)^5, la derivata è f`(x) = 10*2*(2x+5)^9 + 2*5*4 *(4x+3)^4 = 20*(2x+5)^9 + 40*(4x+3)^4.

Immagine titolata Trova l`equazione di una retta tangente Step 2

2. Se tutto va bene, vengono fornite le coordinate in cui la retta tangente incontra la curva. Inserisci il valore x di questo punto, nella funzione derivata, per trovare la pendenza della curva in quel punto.

Per x = 2, il punto sulla curva è (2.27) perché f(2) = 2^3 + 2*2^2 + 5*2 + 1 = 27.

Per f`(x) = 3x^2 + 4x + 5, la pendenza è in (2.27) è f`(2) = 3(2)^2 + 4(2) + 5 = 25.

Immagine titolata Trova l`equazione di una retta tangente Step 3

3. Questa pendenza è anche la pendenza della linea tangente. Ora hai la pendenza e il punto di questa retta, quindi puoi scrivere l`equazione della retta in forma punto-pendenza, oppure y - y1 = m(x - x1).

Nella forma punto-pendenza, è m la pendenza e (x1,y1) sono le coordinate del punto. Quindi in questo esempio, l`equazione diventa y - 27 = 25(x - 2).

Immagine titolata Trova l`equazione di una retta tangente Step 4

4. Potrebbe anche essere necessario convertire questa equazione in un`altra forma per ottenere la risposta finale, se le istruzioni accompagnano il problema lo richiedono.