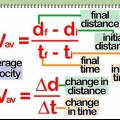
Spostamento = D Lo spostamento è la distanza percorsa da un determinato oggetto. Di solito l`unità di spostamento è indicata in metri. Tempo = T Velocità = v La velocità vettoriale è la velocità di un oggetto in una particolare direzione. Quando calcoliamo la velocità istantanea cerchiamo la velocità di un oggetto in un dato istante t (tempo). La velocità è solitamente indicata in metri al secondo (m/s). Pendenza (o "pendenza") = m Qui può essere utile mostrare il movimento di un oggetto in un semplice grafico x-y con il tempo tracciato lungo l`asse x e lo spostamento lungo l`asse y. Quindi la pendenza della linea in un certo punto è la velocità dell`oggetto. 
La velocità (v) in un dato momento (t) è uguale alla pendenza (tasso di variazione) dell`equazione precedente, dove lo spostamento (d) è tracciato rispetto al tempo (t). 
Una regola generale per trovare la derivata: se y = a*x, allora la derivata è a*n*x. Questa regola si applica a qualsiasi termine del polinomio. La costante (il numero senza una variabile accanto ad essa) scomparirà perché viene moltiplicata per 0. 






Per calcolare la velocità istantanea è necessario calcolare la pendenza di un grafico per un dato punto. 




Il valore a cui si sposta la pendenza quando H si avvicina a 0 è il limite. Questo è uguale alla pendenza della tangente alla curva. La tangente è una retta definita parallela alla parabola su una distanza infinitamente breve. La pendenza della retta tangente è quindi la pendenza della parabola/curva se H diventa una distanza infinitesima sulla retta. L`equazione per trovare la tangente è la derivata dell`equazione della funzione di spostamento, come nella prima parte. 
Calcola la velocità istantanea
Contenuto
La velocità vettoriale (velocità in inglese) è definita come la velocità di un oggetto in una particolare direzione. Per scopi generali, trovare la velocità di un oggetto è semplice come dividere la distanza percorsa per il tempo impiegato per percorrere quella distanza. Ma questo dà solo la velocità media lungo un determinato percorso. Utilizzando equazioni matematiche e derivate è possibile calcolare la velocità dell`oggetto in un dato momento lungo il percorso. Questo è chiamato velocità istantanea. Per comodità e leggibilità, di seguito ci riferiremo alla velocità, sia quando intendiamo velocità "normale" che velocità vettoriale.
Passi
Metodo 1 di 2: Calcolo della velocità istantanea

1. Cosa c`è "velocità istantanea". Gli oggetti che si muovono possono farlo con a velocità costante – cioè muoversi a velocità costante durante tutto il viaggio. Un corridore che corre lungo un campo da calcio mantiene all`incirca la stessa velocità per l`intera lunghezza del campo. Gli oggetti possono anche muoversi con a velocità variabile. Ad esempio, un`auto che percorre una strada con molte curve non avrà sempre la stessa velocità – nelle curve la velocità diminuisce, per poi aumentare nuovamente sui rettilinei.
- Velocità istantanea è una misura della velocità di un oggetto in qualsiasi momento. Ad esempio, la velocità istantanea di un razzo, esattamente un secondo dopo l`accensione del propellente, è molto inferiore alla sua velocità istantanea 30 secondi dopo il decollo, se il razzo ha avuto il tempo di guadagnare velocità.

2. Conosci le tue variabili. Quando si tratta di calcoli di velocità istantanea, ad un certo punto incontrerete quasi sempre determinate variabili. Queste variabili sono:

3. Un esempio. Diciamo che lo spostamento di un oggetto può essere rappresentato da un`equazione: spostamento(i) = 3t + 4t + 7. Il grafico di questa funzione è una linea curva o parabola, dove l`asse x rappresenta il tempo e l`asse y rappresenta lo spostamento.

4. Per calcolare la velocità istantanea di un oggetto con uno spostamento secondo la funzione sopra, abbiamo bisogno della derivata di questa funzione. La derivata di una funzione è uguale alla pendenza della funzione in qualsiasi punto del grafico. Per trovare la derivata, differenziamo la funzione secondo questa formula:

5. Utilizzare questa formula per calcolare la derivata della funzione. Se indichiamo questo come y = 3x + 4x + 7, allora la derivata è (3*2)*x+(4*1)*x+(7*0)*x

6. Semplifica l`equazione. Moltiplicando tutti i termini tra parentesi si ottiene 6x+ 4x+ 0x

7. Continua a semplificare. Questa equazione può essere scritta come 6x + 4. Il "0x" termine diventa quindi uguale a 0, mentre il "4x" termine è semplificato a 4 (n = 1.)

8. Rendi questa nuova funzione uguale alla pendenza m. Usiamo questa funzione derivata per trovare la pendenza dell`equazione originale y = 3x + 4x + 7 per un dato valore di x (tempo). La pendenza originale dell`equazione in un dato momento è la velocità istantanea.

9. Trova la velocità istantanea dell`oggetto per t=4 secondi. Tutto quello che devi fare è inserire il valore del tempo nella variabile x della derivata dell`equazione. Questo dà la seguente equazione y = 6(4) + 4 . Questo è semplificato a 28. La velocità istantanea dell`oggetto per t=4 secondi è 28 m/s.
Metodo 2 di 2: Comprensione di una derivata

1. Disegna un normale sistema di coordinate x-y. Per comprendere correttamente come una derivata può aiutare a trovare la velocità istantanea di un oggetto, una rappresentazione grafica è molto utile. L`asse y rappresenta lo spostamento dell`oggetto, mentre l`asse x rappresenta il tempo.
- Il grafico può continuare sotto l`asse x. Se la linea che rappresenta il movimento dell`oggetto scende al di sotto dell`asse x, significa che l`oggetto si sta muovendo nella direzione inversa e prima del punto iniziale. Di solito il grafico non si estende oltre l`asse y. La velocità non viene misurata per gli oggetti che si spostano indietro nel tempo!
- Se non sei sicuro di come disegnare un grafico o di cosa rappresentano esattamente l`asse x e l`asse y, scopri come può disegnare un grafico di una funzione.

2. Disegna una linea curva, partendo dal punto sulla linea x=0, nella direzione dell`asse x. La pendenza della linea è la velocità con cui y cambia divisa per la velocità con cui x cambia. Quindi, se y è uguale allo spostamento e x è uguale al tempo, la pendenza è uguale alla velocità.

3. Per trovare la pendenza di una retta per un certo punto, utilizziamo un trucco in cui troviamo il limite dell`equazione. Trovare il limite richiede due punti P e Q su una linea curva e trovare la pendenza della linea attraverso entrambi i punti man mano che la distanza tra i due punti diventa sempre più piccola.

4. Scegli un punto P sulla linea. Ad esempio, posiziona P su x=1. La posizione esatta non ha importanza. Scegli un valore conveniente.

5. Scegli un secondo punto Q sulla linea. Q dovrebbe essere a breve distanza da P. Nel nostro esempio, Q è nel punto con x=3, mentre P è nel punto con x=1.

6. Trova la pendenza tra P e Q. La pendenza tra P e Q diventa quindi (la differenza nel valore y di P e Q)/(la differenza nel valore x P e Q). Ci riferiamo a questa differenza nei valori x di P e Q come H. In questo caso H è uguale a 3-1=2.

7. Riduci il valore di H. In altre parole, avvicina Q a P sull`asse x, quindi calcola di nuovo la pendenza tra P e Q. Fallo ripetutamente, ogni volta diminuendo la distanza tra P e Q. Dopo aver calcolato questo alcune volte dovrebbe diventare chiaro che la pendenza si sta avvicinando a un certo valore. Finché H>0 la pendenza non raggiungerà mai questo valore, ma solo di avvicinamento. Diciamo poi che la pendenza il limite si avvicina.

8. Usa le derivate per trovare la pendenza se H rappresenta un intervallo infinitesimo sulla retta. La derivata di un`equazione si trova da "x, è N*x" da applicare a qualsiasi termine dell`equazione originale.
Consigli
- Lo spostamento è come la distanza, ma in una certa direzione, quindi lo spostamento è un vettore e la velocità è una quantità scalare. Lo spostamento può essere negativo mentre la distanza può essere solo positiva.
- Per trovare l`accelerazione (la variazione della velocità nel tempo), usa il metodo della prima parte per trovare la derivata della tua funzione di spostamento. Quindi prendi la derivata di quello. Questo ti dà quindi l`equazione per trovare l`accelerazione in un dato momento: tutto ciò che devi fare è inserire il valore del tempo in questa seconda derivata.
- L`equazione che mette in relazione y (spostamento) con x (tempo) può essere molto semplice, come ad es. y= 6x + 3. In questo caso la pendenza è costante e non è necessario trovare una derivata della pendenza. È uguale a 6, secondo l`equazione lineare y = mx + b.
Articoli sull'argomento "Calcola la velocità istantanea"
Condividi sui social network:
Popolare