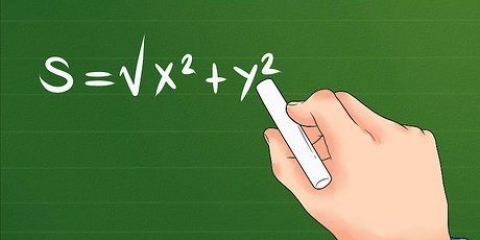Nota, tuttavia, che se le unità di tempo utilizzate nel tuo valore di velocità media sono diverse da quelle nel tuo valore di tempo, dovrai convertire l`una o l`altra in modo che corrisponda. Ad esempio, se una velocità media viene misurata in km/he il tempo è in minuti, dovresti dividere il tempo per 60 per convertirlo in ore. Risolviamo il nostro problema di esempio. 120 km/h × 0,5 h = 60 km. Si noti che le unità di tempo (ore) cadere contro le unità al denominatore della velocità media (ore), lasciando solo le unità di distanza (km). 
Supponiamo di sapere che un`auto ha percorso 60 km in 50 minuti, ma non abbiamo alcun valore per la velocità media durante la guida. In questo caso possiamo usare la variabile sgemma isolare nell`equazione di base per la distanza, e otteniamo sgemma = d/t da ottenere. Quindi calcoliamo 60 km/50 minuti = 1,2 km/min. Nota che nel nostro esempio, la nostra risposta per la velocità ha un`unità insolita (km/minuto). Per ottenere la tua risposta nella forma più comune di km/ora, moltiplicala per 60 minuti/ora e ottieni `72 km/h ottenere. 
Esempio: nel problema di esempio sopra, abbiamo concluso che per percorrere 60 km in 50 minuti, dovremmo viaggiare a 72 km/h. Tuttavia, questo è vero solo se viaggiamo a una velocità per l`intero viaggio. Ad esempio, guidando metà del viaggio a 80 km/h e l`altra metà a 64 km/h, guidiamo ancora 60 km in 50 minuti — 72 km/h = 60 km/50 min = ????? Soluzioni matematiche l`uso delle derivate è spesso una scelta migliore rispetto alla formula della distanza per definire la velocità di un oggetto in situazioni reali, perché sono probabili variazioni di velocità. 

Si noti che questa formula utilizza valori assoluti (il simbolo |). I valori assoluti significano semplicemente che i termini all`interno dei simboli diventano positivi quando sono negativi. Ad esempio, diciamo di fermarci su un tratto di strada perfettamente rettilineo lungo il percorso. Se c`è una cittadina a 5 km di fronte a noi e una città a 1 km dietro di noi, quanto sono distanti le due città?? Se prendiamo la città 1 come x1 = considera 5 e città 2 come x2 = -1, allora possiamo trovare d, la distanza tra le due città, come segue: d = |x2 - X1| = |-1 - 5| = |-6| = 6 km. 
La formula della distanza nello spazio bidimensionale utilizza il teorema di Pitagora, che afferma che l`ipotenusa di un triangolo rettangolo è uguale alla radice quadrata degli altri due lati. Ad esempio, supponiamo di avere due punti nel piano x-y: (3, -10) e (11, 7) che rappresentano rispettivamente il centro di una circonferenza e un punto sulla circonferenza. Per trovare la distanza diritta tra questi due punti, possiamo risolvere quanto segue: d = √((x2 - X1) + (s2 - y1)) d = √((11 - 3) + (7 - -10)) d = √(64 + 289) d = √(353) = 18.79 
Esempio: diciamo che come un astronauta in bilico nello spazio vicino a due asteroidi. Uno è a circa 8 km davanti a noi, 2 km alla nostra destra e 5 km sotto di noi, mentre l`altro è a 3 km dietro di noi, 3 km alla nostra sinistra e 4 km sopra di noi. Se rappresentiamo le posizioni di questi asteroidi con le coordinate (8.2,-5) e (-3,-3.4), possiamo trovare la distanza tra i due come segue: d = √((-3 - 8) + (-3 - 2) + (4 - -5)) d = √((-11) + (-5) + (9)) d = √(121 + 25 + 81) d = √(227) =15,07 km
Calcola distanza
Contenuto
Distanza, spesso indicata come variabile D, è una misura dello spazio occupato da una retta tra due punti. La distanza può riferirsi allo spazio tra due punti stazionari (ad esempio, l`altezza di una persona è la distanza dalla parte inferiore dei suoi piedi alla sommità della sua testa) o può riferirsi allo spazio tra la posizione attuale di una persona in movimento oggetto e la sua posizione iniziale. La maggior parte dei problemi di distanza può essere risolta con le equazioni d = sgemma × t dove d è la distanza, sgemma la velocità media et il tempo o l`equazione d = √((x2 - X1) + (s2 - y1)), dove (x1, y1) e (x2, y2) sono le coordinate xey di due punti.
Passi
Metodo 1 di 2: Determina la distanza con velocità e tempo medi

1. Determina i valori per la velocità e il tempo medi. Quando si cerca di trovare la distanza percorsa da un oggetto in movimento, due informazioni sono fondamentali per effettuare questo calcolo: il velocità` (o intensità della velocità) e ilvolta dove l`oggetto è stato spostato. Con questi dati è possibile trovare la distanza percorsa dall`oggetto, utilizzando la formula d = sgemma × t.
- Per comprendere meglio l`applicazione della formula della distanza, in questa sezione risolveremo un problema di esempio. Diciamo che stiamo guidando a circa 120 km/h e vogliamo sapere quanto percorreremo in mezz`ora. Di 120 km/h come il nostro valore per la velocità media e 0,5 ore come nostro valore per il tempo, risolveremo questo problema nel passaggio successivo.

2. Moltiplica la velocità media per il tempo. Una volta che conosci la velocità media di un oggetto in movimento e il tempo impiegato per spostarsi, trovare la distanza che ha percorso è relativamente facile. Basta moltiplicare questi due valori insieme per ottenere la risposta.

3. Modifica l`equazione da risolvere per le altre variabili. La semplicità dell`equazione di base della distanza (d = sgemma × t) rende abbastanza facile utilizzare l`equazione per trovare i valori delle variabili oltre alla distanza. Isola la variabile che vuoi risolvere secondo le regole di base di matematica, e poi inserisci i valori delle altre due variabili, per trovare il valore della terza. In altre parole, per trovare la velocità media del tuo oggetto, usa l`equazione Sgemma = g/t e per trovare il tempo che un oggetto ha viaggiato, usa l`equazione t = d/sgemma.

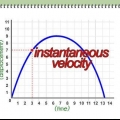
4. Si noti che la variabile `sgemma` nella formula della distanza si riferisce media velocità. È importante capire che la formula della distanza standard fornisce un`immagine semplificata del movimento di un oggetto. La formula della distanza presuppone che l`oggetto in movimento abbia a velocità costante ha — in altre parole, presuppone che l`oggetto in movimento si muova a una velocità "uniforme", immutabile. Per problemi di matematica astratti, come quelli incontrati in ambito accademico, a volte è ancora possibile modellare il movimento di un oggetto utilizzando questa ipotesi. Nella vita reale, però, questo modello spesso non rappresenta accuratamente il movimento di oggetti in movimento, che in realtà possono accelerare, decelerare, fermarsi e invertire nel tempo.
Metodo 2 di 2: Determinazione della distanza tra due punti

1. Determinazione di due punti in uno spazio piatto. E se invece di determinare la distanza percorsa da un oggetto in movimento, fosse necessario determinare la distanza tra due oggetti fissi? In casi come questo, la formula della distanza basata sulla velocità sopra descritta non sarà di alcuna utilità. Fortunatamente, esiste un`altra formula della distanza per trovare rapidamente la distanza più breve tra due punti. Tuttavia, per questa formula è necessario conoscere le coordinate dei due punti. Se hai a che fare con una distanza unidimensionale (come su una linea numerica), le tue coordinate sono due numeri, x1 e x2. Se hai a che fare con la distanza in due dimensioni, allora hai bisogno di valori per due punti (x,y), (x1,y1) e (x2,y2). Infine, per tre dimensioni sono necessari valori per (x1,y1,z1) e (x2,y2,z2).

2. Determina la distanza su una retta sottraendo il valore delle coordinate dei due punti. Calcolare la distanza unidimensionale tra due punti se si conosce il valore di ciascun punto è facile. Basta usare la formula d = |x2 - X1|. In questa formula sottrarre x1 fuori di x2 e prendi il valore assoluto della tua risposta per trovare la distanza tra x1 e x2 trovare. Normalmente si usa la formula della distanza unidimensionale quando i due punti giacciono su una linea o un asse dei numeri.

3. Trova la distanza nell`aereo usando il teorema di Pitagora. Trovare la distanza tra due punti nello spazio bidimensionale è più complicato che in una dimensione, ma non difficile. Basta usare la formula d = √((x2 - X1) + (s2 - y1)). In questa formula, sottrai le due coordinate x, al quadrato il risultato, sottrai le coordinate y, al quadrato il risultato, aggiungi i due risultati intermedi e calcoli la radice quadrata per trovare la distanza tra i due punti da trovare. Questa formula funziona sul piano bidimensionale, ad esempio sui grafici x/y standard.

4. Determina la distanza tridimensionale modificando la formula dell`area. In tre dimensioni, i punti hanno anche una coordinata z oltre alle coordinate x e y. Per trovare la distanza tra due punti nello spazio tridimensionale, utilizzare d = √((x2 - X1) + (s2 - y1) + (z2 - z1)). Questa è una forma modificata della formula della distanza bidimensionale sopra descritta che tiene conto anche delle coordinate z. Sottraendo le due coordinate z l`una dall`altra, posizionandole nel quadrato e scorrendo il resto della formula come descritto sopra, puoi essere sicuro che la tua risposta finale rifletta la distanza tridimensionale tra i due punti.
Articoli sull'argomento "Calcola distanza"
Condividi sui social network:
Popolare