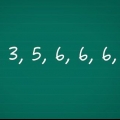Calcolo della Covarianza

Contenuto

Passi
Avvertenze

La covarianza è un calcolo statistico per rendere più trasparente la relazione tra due insiemi di dati. Supponiamo, ad esempio, che gli antropologi studino l`altezza e il peso di una popolazione all`interno di una particolare cultura. Per ogni persona nello studio, altezza e peso possono essere rappresentati con una coppia di dati (x, y). Questi valori possono essere utilizzati in una formula standard per il calcolo della relazione di covarianza. Questo articolo spiega innanzitutto i calcoli per determinare la covarianza di un set di dati. Successivamente, verranno discussi altri due modi automatizzati per determinare il risultato.

Passi

Metodo 1 di 4: calcolo manuale della covarianza utilizzando la formula standard

Immagine titolata Calculate Covariance Step 1

1. Impara la formula di covarianza standard e le sue parti. La formula standard per il calcolo della covarianza è

Σ (X io - X_{media}) (y_{io} - y_{media}) / (n - 1)

$Sigma (x_{i}-x_{{text{avg}}})(y_{i}-y_{{text{avg}}})/(n-1)$ . Per utilizzare questa formula, è necessario conoscere il significato delle variabili e dei simboli:

$Σ$ $Sigma$ - Questo simbolo è la lettera greca `sigma`. Nelle funzioni matematiche, questo significa aggiungere una serie di quanto segue. In questa formula il segno Σ significa che si calcolano i valori al numeratore della frazione, quindi si sommano tutti insieme, quindi si divide il totale per il denominatore.
$X io$ $x_{i}$ - Puoi leggere questa variabile come `x sub i`. Il pedice i rappresenta un contatore. Significa che eseguirai un calcolo per ogni valore di x nel tuo set di dati.
$X un v G$ $x_{{media}}$ - `avg` indica che x(avg) è il valore medio di tutti x punti dati. La media a volte viene scritta come una x con una breve linea orizzontale sopra di essa. In quello stile, leggi la variabile come "x-bar", ma significa comunque la media del set di dati.
$y io$ $y_{i}$ - Puoi leggere questa variabile come `y sub i`. Il pedice i è il numeratore. Significa che eseguirai un calcolo per ogni valore di y nel tuo set di dati.
$y un v G$ $y_{{media}}$ - `avg` indica che y(avg) è il valore medio di tutti x punti dati. La media è talvolta scritta come una y con una breve linea orizzontale sopra di essa. In quello stile leggi la variabile come `y-bar`, ma significa comunque la media del set di dati.
$n$ $n$ - Questa variabile è il numero di elementi nel tuo set di dati. Ricorda che in un problema di covarianza, un singolo `elemento` è composto sia da un valore x che da un valore y. Il valore `n` è il numero di coppie di punti dati, non i singoli numeri.

Immagine titolata Calculate Covariance Step 2

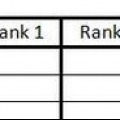
2. Costruisci la tua tabella dati. Prima di iniziare, è utile raccogliere i tuoi dati. Crea una tabella con cinque colonne. È necessario dichiarare ciascuna colonna come segue:

X

$X$ - Riempi questa colonna con i valori dei punti dei dati x.

y

$y$ - Riempi questa colonna con i valori dei dati y. Assicurati che i valori y siano allineati con i valori x corrispondenti. In un problema di covarianza, l`ordine dei punti dati e l`accoppiamento di xey sono importanti.

(X io - X_{media})

$(x_{i}-x_{{text{avg}}})$ - Lascia vuota questa colonna all`inizio. Lo riempirai di dati dopo aver calcolato la media dei dati x.

(y io - y_{media})

$(y_{i}-y_{{text{avg}}})$ - Lascia vuota questa colonna all`inizio. Lo riempirai di dati dopo aver calcolato la media dei dati y.

Prodotto

${text{Prodotto}}$ - Lascia vuota anche l`ultima colonna. Questo sarà compilato durante l`elaborazione dell`incarico.

Immagine titolata Calculate Covariance Step 3

3. Calcola la media degli x punti dati. Questa raccolta di dati di esempio contiene 9 numeri. Per trovare la media, sommali e dividi la somma per 9. Questo dà il risultato 1 + 3 + 2 + 5 + 8 + 7 + 12 + 2 + 4 = 44. Quando dividi questo per 9 ottieni la media 4,89. Questo è il valore che utilizzerai come x(avg) per i prossimi calcoli.

Immagine titolata Calculate Covariance Step 4

4. Calcola la media dei punti dati y. Questa colonna y deve anche essere composta da 9 punti dati che coincidono con i punti dati x. Determina la media di questo. Per questo set di dati di esempio, diventa 8 + 6 + 9 + 4 + 3 + 3 + 2 + 7 + 7 = 49. Dividi questo totale per 9 per ottenere una media di 5,44. Utilizzerai 5,44 come valore di y(avg) per i calcoli imminenti.

Immagine titolata Calculate Covariance Step 5

5. Calcola i valori (Xio-Xmedia){displaystyle (x_{i}-x_{text{avg}})} $(x_{i}-x_{{text{avg}}})$ . Per ogni elemento nella colonna x, calcola la differenza tra quel numero e il valore medio. Per questo problema di esempio, ciò significa sottrarre 4,89 da ogni valore x. Se il punto dati originale è inferiore alla media, il risultato sarà negativo. Se il punto dati originale è maggiore della media, il risultato sarà positivo. Assicurati di tenere traccia di quali valori sono negativi.

Ad esempio, il primo punto dati nella colonna x è 1. Il valore da inserire nella prima riga della colonna

(X io - X_{media})

$(x_{i}-x_{{text{avg}}})$ è: 1 – 4,89 = -3,89.

Ripetere questo processo per ogni punto dati. Quindi la seconda riga diventa: 3 - 4,89 = -1.89. La terza riga diventa: 2 - 4,89 = -2,89. Continua questo processo per tutti i punti dati. I nove numeri in questa colonna diventano: -3.89, -1.89, -2.89, 0.11, 3.11, 2.11, 7.11, -2.89, -0.89.

Immagine titolata Calculate Covariance Step 6

6. Calcola i valori (yio-ymedia){displaystyle (y_{i}-y_{text{avg}})} $(y_{i}-y_{{text{avg}}})$ . In questa colonna, eseguirai sottrazioni simili, usando i punti dati y e il significato di y. Se il punto dati originale è inferiore alla media, il risultato sarà negativo. Se il punto dati originale è maggiore della media, il risultato sarà positivo. Assicurati di tenere traccia di quali valori sono negativi.

Quindi per la prima riga il tuo calcolo sarà: 8 -5,44, = 2,56.

La seconda riga diventa: 6 – 5,44 = 0,56.

Continua a sottrarre i valori fino alla fine dell`elenco dei dati. Quando hai finito, dovresti avere i seguenti nove valori in questa colonna: 2.56, 0.56, 3.56, -1.44, -2.44, -2.44, -3.44, 1.56, 1.56.

Immagine titolata Calculate Covariance Step 7

7. Calcola i prodotti per ogni riga di dati. Riempi le righe dell`ultima colonna moltiplicando i numeri che hai calcolato nelle due colonne precedenti di

(X io - X_{media})

$(x_{i}-x_{{text{avg}}})$ e

(y io - y_{media})

$(y_{i}-y_{{text{avg}}})$ . Procedi riga per riga, moltiplicando i due numeri per i punti dati corrispondenti. Fai attenzione a eventuali valori negativi lungo la strada.

Nella prima riga di questi dati di esempio, il

(X io - X_{media})

$(x_{i}-x_{{text{avg}}})$ hai calcolato -3,89 e il

(y io - y_{media})

$(y_{i}-y_{{text{avg}}})$ valore 2,56. Il prodotto di questi due numeri è: -3,89 x 2,56 = -9,96.

Per la seconda riga, moltiplica i due numeri: -1,88 x 0,56 = -1,06.

Continua a moltiplicare riga per riga fino alla fine del set di dati. Al termine, i nove valori in questa colonna dovrebbero essere: -9,96, -1,06, -10,29, -0,16, -7,59, -5,15, -24,46, -4,51, -1,39.

Immagine titolata Calculate Covariance Step 8

8. Trova la somma dei valori nell`ultima colonna. È qui che entra in gioco il simbolo Σ. Dopo aver eseguito tutti i calcoli finora, somma i risultati. Per questo set di dati di esempio dovresti ora avere nove valori nell`ultima colonna. Somma quei nove numeri insieme. Presta molta attenzione al fatto che un numero sia positivo o negativo.

La somma di questo set di dati di esempio dovrebbe essere -64,57. Scrivi questo totale nello spazio in fondo alla colonna. Questo è il valore del numeratore della formula di covarianza standard.

Immagine titolata Calculate Covariance Step 9

9. Calcola il denominatore della formula di covarianza. Il numeratore della formula di covarianza standard è il valore appena calcolato. Il denominatore è rappresentato da (n-1) ed è uno in meno rispetto al numero di coppie di dati nel tuo set di dati.

In questo problema di esempio, ci sono nove coppie di dati, quindi n è 9. Pertanto, il valore di (n-1) è uguale a 8.

Immagine titolata Calculate Covariance Step 10

10. Dividi il numeratore per il denominatore. L`ultimo passaggio per calcolare la covarianza è dividere il numeratore,

Σ (X io - X_{media}) (y_{io} - y_{media})

$Sigma (x_{i}-x_{{text{avg}}})(y_{i}-y_{{text{avg}}})$ dal denominatore,

(n - 1)

$(n-1)$ . Il quoziente è la covarianza dei tuoi dati.

Per questo set di dati di esempio, questo calcolo è: -64,57/8 = -8,07.

Metodo 2 di 4: calcola la covarianza utilizzando un foglio di lavoro Excel

Immagine titolata Calculate Covariance Step 11

1. Nota quali sono i calcoli ripetitivi. La covarianza è un calcolo che devi fare a mano un paio di volte per capire il significato del risultato. Tuttavia, se hai intenzione di utilizzare regolarmente la covarianza per interpretare i dati, allora hai bisogno di un modo più veloce e automatizzato per ottenere i risultati. Potresti aver notato che con il nostro set di dati relativamente piccolo di sole nove coppie di dati, i calcoli consistevano in due medie, diciotto sottrazioni separate, nove moltiplicazioni, un`addizione e infine un`altra divisione. Sono 31 calcoli relativamente piccoli per trovare la soluzione. Lungo la strada, corri il rischio di perdere i segni negativi o di copiare i risultati in modo errato, causando una risposta errata.

Immagine titolata Calculate Covariance Step 12

2. Creare un foglio di lavoro per il calcolo della covarianza. Se hai familiarità con Excel (o qualsiasi altro programma di calcolo), puoi facilmente creare una tabella per determinare la covarianza. Etichetta le intestazioni delle cinque colonne come nei calcoli manuali: x, y, (x(i)-x(avg)), (y(i)-y(avg)) e Product.

Per semplificare la denominazione, dai un nome alla terza colonna come "differenza x" e alla quarta colonna "differenza y", purché ricordi il significato dei dati.

Se la tabella inizia nell`angolo in alto a sinistra del foglio di lavoro, la cella A1 verrà etichettata come x, mentre le altre etichette continueranno alla cella E1.

Immagine titolata Calculate Covariance Step 13

3. Compila i punti dati. Digita i valori dei dati nelle due colonne x e y. Ricorda che l`ordine dei punti dati è importante, quindi devi abbinare ogni y con il valore corrispondente di x.

I valori x iniziano nella cella A2 e continuano fino al numero di punti dati necessari.

I valori y iniziano nella cella B2 e continuano fino al numero di punti dati necessari.

Immagine titolata Calculate Covariance Step 14

4. Determina le medie dei valori xey. Excel calcola le medie per te molto rapidamente. Nella prima cella vuota sotto ogni colonna di dati, digita la formula =MEDIA (A2:A___). Riempi lo spazio vuoto con il numero della cella che corrisponde al tuo ultimo punto dati.

Ad esempio, se hai 100 punti dati, le celle da A2 a A101 verranno riempite, quindi nella cella dovrai digitare: = MEDIA(A2:A101).

Per i dati y, digita la formula = MEDIA(B2:B101).

Ricorda che una formula in Excel inizia con un segno `=`.

Immagine titolata Calculate Covariance Step 15

5. Digita la formula per la colonna (x(i)-x(avg)). Nella cella C2, inserisci la formula per calcolare la prima sottrazione. Questa formula diventa: =A2-___. Riempi lo spazio vuoto con l`indirizzo della cella che contiene la media dei dati x.

Ad esempio, la media dei 100 punti dati viene calcolata nella cella A103, quindi la formula diventa: =A2-A103.

Immagine titolata Calculate Covariance Step 16

6. Ripetere la formula per i punti dati (y(i)-y(avg)). Seguendo lo stesso esempio sarà nella cella D2. La formula diventa: =B2-B103.

Immagine titolata Calculate Covariance Step 17

7. Digita la formula per la colonna "Prodotto". Nella quinta colonna devi digitare nella cella E2 la formula per calcolare il prodotto delle due celle precedenti. Questo diventa quindi: =C2*D2.

Immagine titolata Calculate Covariance Step 18

8. Copia le formule per riempire la tabella. Finora hai programmato solo i primi punti dati nella riga 2. Usando il mouse, evidenzia le celle C2, D2 ed E2. Posiziona il cursore sulla piccola casella nell`angolo in basso a destra finché non viene visualizzato un segno più. Fare clic e tenere premuto il pulsante del mouse e trascinare il mouse verso il basso per espandere la selezione e riempire l`intera tabella di dati. Questo passaggio copierà automaticamente le tre formule dalle celle C2, D2 ed E2 nell`intera tabella. La tabella dovrebbe essere riempita automaticamente con tutti i calcoli.

Immagine titolata Calculate Covariance Step 19

9. Programma la somma dell`ultima colonna. È necessaria la somma degli articoli nella colonna "Prodotto". Nella cella vuota immediatamente sotto l`ultimo punto dati in quella colonna, digita la formula: =SUM(E2:E___). Riempi lo spazio vuoto con l`indirizzo della cella dell`ultimo punto dati.

Nell`esempio con 100 punti dati, questa formula va nella cella E103. Tipo: =SOMMA(E2:E102).

Immagine titolata Calculate Covariance Step 20

10. Determina la covarianza. Puoi anche lasciare che Excel esegua il calcolo finale per te. L`ultimo calcolo nella cella E103 nel nostro esempio rappresenta il numeratore della formula di covarianza. Immediatamente sotto quella cella, digita la formula: =E103/___. Riempi lo spazio vuoto con il numero di punti dati che hai. Nel nostro esempio questo è 100. Il risultato è la covarianza dei tuoi dati.

Metodo 3 di 4: utilizzo dei calcolatori di covarianza online

Immagine titolata Calculate Covariance Step 21

1. Cerca online i calcolatori di covarianza. Varie scuole, aziende o altre fonti hanno siti Web che calcolano i valori di covarianza molto facilmente per te. Utilizzare il termine di ricerca "calcolatore di covarianza" in un motore di ricerca.

Immagine titolata Calculate Covariance Step 22

2. Inserisci i tuoi dati. Si prega di leggere attentamente le istruzioni sul sito Web per assicurarsi di inserire le informazioni correttamente. È importante che le tue coppie di dati siano mantenute in ordine, altrimenti il risultato generato sarà una covarianza errata. I siti Web hanno stili di immissione dei dati diversi.

Sul sito http://ncalcolatori.com/statistics/calcolatore di covarianza.htm, ad esempio c`è una casella orizzontale per inserire i valori x e una seconda casella orizzontale per inserire i valori y. Devi inserire i tuoi dati separati da virgole. Quindi, il set di dati x calcolato in precedenza in questo articolo dovrebbe quindi essere inserito come 1,3,2,5,8,7,12,2,4. I dati y come 8,6,9,4,3,3,2,7,7.

Su un altro sito, https://www.la calcolatrice.co/math/Covariance-Calculator-705.html, ti verrà chiesto di inserire i dati x nella prima casella. I dati vengono inseriti verticalmente, con un elemento per riga. Pertanto, la voce su questo sito è simile a:

Immagine titolata Calculate Covariance Step 23

3. Calcola i tuoi risultati. La cosa interessante di questi calcoli online è che dopo aver inserito i dati di solito devi solo fare clic sul pulsante "Calcola", dopodiché i risultati vengono visualizzati automaticamente. La maggior parte dei siti fornisce i calcoli intermedi di x(avg), y(avg) e n.

Metodo 4 di 4: Interpretazione dei risultati della covarianza

Immagine titolata Calculate Covariance Step 24

1. Cerca una relazione positiva o negativa. La covarianza è un singolo numero statistico che indica la relazione tra un set di dati e l`altro. Nell`esempio citato nell`introduzione, vengono misurati l`altezza e il peso. Ti aspetteresti che man mano che le persone crescono, anche il loro peso aumenterà, portando a una visione di covarianza positiva. Un altro esempio: supponiamo che vengano raccolti dati che indicano il numero di ore in cui una persona ha praticato il golf e il punteggio che ottiene. In questo caso, ti aspetti una covarianza negativa, il che significa che all`aumentare del numero di ore di allenamento, il punteggio del golf diminuirà. (Nel golf, un punteggio più basso è migliore).

Considera il set di dati di esempio calcolato sopra. La covarianza risultante è -8,07. Il segno meno significa che all`aumentare dei valori x, i valori y tendono a diminuire. Puoi vedere che questo è vero osservando alcuni dei valori. Ad esempio, i valori x di 1 e 2 corrispondono ai valori y di 7, 8 e 9. I valori x di 8 e 12 sono legati ai valori y di 3 e 2 rispettivamente.

Immagine titolata Calculate Covariance Step 25

2. Interpreta la dimensione della covarianza. Se il numero del punteggio di covarianza è grande, un numero grande positivo o un numero grande negativo, puoi interpretarlo come due elementi di dati fortemente collegati, in modo positivo o negativo.

La covarianza -8,07 del set di dati campione è piuttosto ampia. Si noti che i dati vanno da 1 a 12. Quindi 8 è un numero piuttosto grande. Ciò indica una relazione abbastanza forte tra i set di dati x e y.

Immagine titolata Calculate Covariance Step 26

3. Comprendi la mancanza di una relazione. Se il tuo risultato è una covarianza uguale o molto vicina a 0, puoi concludere che i punti dati non hanno alcuna relazione. Cioè, un aumento di un valore può, ma non deve portare a un aumento dell`altro. I due termini sono collegati quasi arbitrariamente.

Supponiamo di mettere in relazione le taglie delle scarpe con i voti degli esami. Poiché ci sono così tanti fattori che influenzano i voti degli esami di uno studente, è prevedibile un punteggio di covarianza vicino a 0. Ciò indica che non c`è quasi nessuna relazione tra i due valori.

Immagine titolata Calculate Covariance Step 27

4. Visualizza graficamente la relazione. Per comprendere visivamente la covarianza, puoi tracciare i tuoi punti dati in un grafico x,y. Quando lo fai, dovresti vedere abbastanza facilmente che i punti, sebbene non siano esattamente in linea retta, tendono ad avvicinarsi a un gruppo in una linea diagonale dall`alto a sinistra verso il basso a destra. Questa è la descrizione di una covarianza negativa. Vedi anche che il valore della covarianza è -8,07. Questo è un numero piuttosto elevato rispetto ai punti dati. Il numero elevato suggerisce che la covarianza è abbastanza forte, che può essere dedotta dalla forma lineare dei punti dati.

Per rivederlo, leggi gli articoli di wikiHow sul disegno di punti in un sistema di coordinate.

Avvertenze

La covarianza ha un`applicazione limitata nelle statistiche. È spesso un passo verso il calcolo dei coefficienti di correlazione o altri concetti. Fai attenzione alle interpretazioni eccessivamente audaci basate su un punteggio di covarianza.

Articoli sull'argomento "Calcola la covarianza"

Calcola il coefficiente di correlazione del rango di spearman

Calcola varianza

Calcola frequenza cumulativa

Calcola distanza

Condividi sui social network: