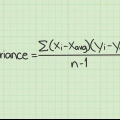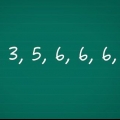Calcolo della Varianza: 8 Passaggi (con Immagini)

Contenuto

Passi
Consigli

Il calcolo della varianza consente di misurare la dispersione di un insieme di valori: il grado in cui un numero di valori differisce l`uno dall`altro. La varianza è una delle componenti della distribuzione di probabilità e indica la misura in cui i valori si discostano dalla media. La varianza viene spesso utilizzata insieme alla deviazione standard (la radice quadrata della varianza). Se vuoi sapere come calcolare la varianza di un insieme di valori, segui i passaggi seguenti.

Passi

1. Scrivi la formula per calcolare la varianza. La stima per calcolare una stima casuale della varianza della popolazione da un campione fisso di n osservazioni è la seguente definizione:(s) = Σ [(x_io - x̅)]/n - 1. La formula per calcolare la varianza in un`intera popolazione è la stessa della precedente, tranne per il fatto che il denominatore non è uguale a n – 1, ma a n. Finché hai a che fare con un insieme finito di osservazioni, è meglio usare la prima formula. Ecco una spiegazione delle variabili della formula:

s = varianza
Σ = Somma, la somma di tutti i termini nell`equazione dopo il segno della somma.
X_io = I valori del campione.
x̅ = La media dei valori nella serie.
n = La dimensione del campione. Il numero di valori nella serie.

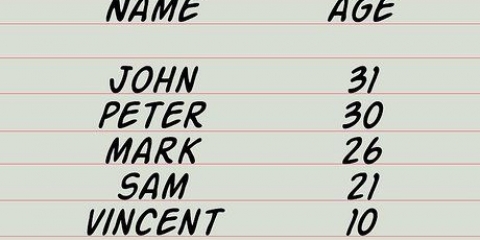
2. Calcola la somma dei valori nella serie. Per prima cosa creare una tabella con una colonna per i valori, il valore meno la media (x_io - x̅) e quindi il quadrato di questi termini [(x_io - X))]. Dopo aver finito con la tabella e aver popolato la prima colonna, somma tutti i valori della serie. Supponiamo di avere a che fare con la seguente sequenza di numeri: 17, 15, 23, 7, 9, 13. Sommato questo è: 17 + 15 + 23 + 7 + 9 + 13 = 84.

3. Calcola la media. Dividi la somma dei numeri della serie per il numero di elementi della serie per calcolare la media. Quindi in questo caso la somma 84 divisa per il numero di numeri, 6. 84/6 = 14. scrivere "14" in fondo alla colonna come media.

4. Sottrarre la media di ogni valore della serie. Sottrarre 14 da ogni valore della serie e compilare la terza colonna (la media campionaria). Puoi controllare il tuo lavoro controllando se la somma di tutti i risultati è zero. Ecco come calcolare la deviazione dalla media per ogni valore della serie:

17 - 14 = 3

15 - 14 = 1

23 - 14 = 9

7 - 14 = -7

9 - 14 = -5

13 - 14 = -1

5. Piazza ogni risultato. Dopo aver calcolato la deviazione dalla media, quadrala e scrivi la risposta nella quarta colonna. Quindi tutte le risposte sono positive. Ecco come ha funzionato:

3 = 9

1 = 1

9 = 81

(-7)= 49

(-5) = 25

(-1)= 1

6. Calcola la somma dei quadrati. Somma i risultati insieme. 9 + 1 + 81 + 49 + 25 + 1 = 166

7. Sostituisci i valori nell`equazione. Compila i valori nell`equazione. Ricordati che "n" rappresenta il numero di elementi nella sequenza.

s = 166/(6-1)

8. Risolvere. Ora dividi 166 per 5. Il risultato è 33.2. Se vuoi anche conoscere la deviazione standard, trova la radice quadrata di 33,2. √33,2 = 5,76. Ora puoi iniziare a interpretare questi dati in relazione al quadro generale. Di solito viene confrontata la varianza di due serie. Il valore più basso significa che in quella serie la varianza è minore.

Consigli

Poiché può essere difficile interpretare la varianza, questo valore viene solitamente calcolato solo come inizio del calcolo della deviazione standard.