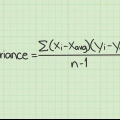Se la misura sperimentale è di 60 cm, anche il calcolo dell`imprecisione dovrà essere arrotondato a un numero intero. Ad esempio, l`imprecisione di questa misurazione può essere 60 cm ± 2 cm, ma non 60 cm ± 2.2 cm. Se la tua lettura sperimentale è uguale a 3.4 cm, quindi anche l`imprecisione dovrà essere arrotondata a 0,1 cm. Ad esempio, l`imprecisione di questa misurazione può essere 3.4 cm ± .essere 1 cm, ma non 3.4 cm ± 1 cm. 
Osserva da vicino il bordo della palla e il righello per avere un`idea di quanto possa essere affidabile la tua misurazione. In un righello standard, i segni di 0,5 cm sono chiaramente contrassegnati, ma supponiamo che tu possa avvicinarti un po` di più. Se sembra che tu possa ottenere entro 0,3 cm con la tua misurazione, l`imprecisione è 0,3 cm. Ora misureremo il diametro della palla. Supponiamo di ottenere 7,6 cm come risposta. Ora annota la misura stimata con l`imprecisione. Il diametro della palla è 7,6 cm ± 0,3 cm. 
Supponiamo di non poter avvicinarti di molto di 0,2 cm con un righello normale. Quindi, l`imprecisione è di ± 0,2 cm. Supponiamo di aver misurato che la pila di scatole insieme è di 22 cm. Ora tutto ciò che devi fare è dividere questo valore di misurazione e l`imprecisione per 10 (il numero di caselle). 22 cm/10 = 2,2 cm e 0,2 cm/10 = 0,02 cm. Ciò significa che lo spessore di 1 scatola è pari a 2,20 cm ± 0,02 cm. 



0,43 s – 0,42 s = 0,01 s 0,52 s - 0,42 s = 0,1 s 0,35 s - 0,42 s = -0,07 s 0,29 s - 0,42 s = -0,13 s 0,49 s - 0,42 s = 0,07 s Ora aggiungi i quadrati delle differenze: (0,01 s) + (0,1 s) + (-0,07 s) + (-0,13 s) +(0,07 s)= 0,037 s. Trova la media di questi quadrati aggiunti dividendo il risultato per 5. 0,037 s/5 = 0,0074 s. 



(10 cm ± .4 cm) - (3 cm ± .2 cm) = (10 cm - 3 cm) ± (.4 cm +. 2 cm) = 7 cm ± 0,6 cm (6 cm ± 0,2 cm) = (0,2 / 6) x 100 e aggiungi un segno % ad esso. Questo è il 3,3%
Così:
(6 cm ± 0,2 cm) x (4 cm ± 0,3 cm) = (6 cm ± 3,3%) x (4 cm ± 7,5%) (6 cm x 4 cm) ± (3.3 + 7,5) = 24 cm ± 10,8% = 24 cm ± 2,6 cm (10 cm ± 0,6 cm) ÷ (5 cm ± 0,2 cm) = (10 cm ± 6%) ÷ (5 cm ± 4%) (10 cm ÷ 5 cm) ± (6% + 4%) = 2 cm ± 10% = 2 cm ± 0,2 cm 
(2,0 cm ± 1.0 cm) = (2,0 cm) ± (1,0 cm) x 3 = 8,0 cm ± 3 cm
Calcola imprecisione
Contenuto
Quando si effettua una misurazione durante la raccolta dei dati, si può presumere che ci sia a "valore reale" rientra nell`intervallo delle misurazioni che hai effettuato. Se vuoi calcolare l`inesattezza delle tue letture, dovrai trovare la migliore stima della tua lettura e tenerne conto quando sottrai o aggiungi l`imprecisione della lettura.
Passi
Metodo 1 di 3: imparare le basi

1. Determinare la forma corretta per l`imprecisione. Supponiamo di misurare la lunghezza di un bastoncino di circa 4,2 cm, con un margine di 1 millimetro. Ciò significa che lo stick è quasi sicuramente di 4,2 cm, ma può essere leggermente più grande o più piccolo di questa lunghezza, con un margine di errore di 1 millimetro.
- Registrarlo come segue: 4,2 cm ± 0,1 cm. Puoi riscriverlo come: 4,2 cm ± 1 mm, perché 0,1 cm = 1 mm.

2. Arrotonda la lettura sperimentale allo stesso numero di cifre decimali dell`imprecisione. Le misurazioni che comportano imprecisioni sono generalmente arrotondate a 1 o 2 cifre significative. Il punto chiave è che si arrotondano le misurazioni dell`esperimento allo stesso numero di cifre decimali dell`imprecisione, per mantenere le misurazioni coerenti.

3. Calcola l`imprecisione di una singola misurazione. Supponiamo di misurare il diametro di una palla rotonda con un righello. Questo è complicato perché è difficile individuare esattamente dove si trova il bordo esterno della pallina e come misurarlo con il righello. Supponiamo che il righello possa trovare il diametro con una precisione di 0,1 cm - questo non significa che puoi misurare il diametro della palla con quel livello di precisione.

4. Calcola l`imprecisione di una singola misurazione di più oggetti. Supponiamo di misurare l`altezza di una pila di 10 custodie per CD che hanno tutte dimensioni. Supponiamo di voler sapere qual è lo spessore di 1 scatola. Questa lettura è così piccola che la percentuale di imprecisione sarà alta. Ma se misuri 10 scatole, puoi dividere il risultato e dividere semplicemente la sua imprecisione per il numero di scatole nella pila per trovare lo spessore di 1 scatola.

5. Eseguire questa misurazione più volte. Per aumentare l`accuratezza della tua misurazione, che tu stia misurando la lunghezza di un oggetto o il tempo impiegato per percorrere una certa distanza, aumenterai le possibilità di una misurazione accurata se esegui misurazioni multiple. Determinare la media di tutte le misurazioni si tradurrà in definitiva in una migliore determinazione dell`imprecisione di una misurazione.
Metodo 2 di 3: calcolo dell`imprecisione di misurazioni multiple

1. Prendi più misurazioni. Supponiamo di voler calcolare quanto tempo impiega una palla a cadere dal tavolo sul round. Per ottenere i migliori risultati, dovrai eseguire la stessa misurazione almeno un paio di volte, diciamo che lo facciamo cinque volte. Quindi dovrai calcolare la media di queste 5 misurazioni e quindi aggiungere o sottrarre la deviazione standard da questa, per il miglior risultato.
- Supponiamo di avere le seguenti letture: 0,43 s, 0,52 s, 0,35 s, 0,29 s e 0,49 s.

2. Determina la media delle misurazioni. Puoi farlo sommando tutti e cinque insieme e dividendo la somma per 5, il numero di valori misurati. 0,43 s + 0,52 s + 0,35 s + 0,29 s + 0,49 s = 2.08 sec. Condividi ora 2.08 per 5. 2.08/5 = 0,42 sec. La media è 0,42 s.

3. Determina la varianza di queste misurazioni. Puoi farlo determinando la differenza tra ciascuna delle 5 misurazioni e la media. Sottrarre le letture da 0,42 s. Ecco le 5 differenze:

4. Determina la deviazione standard. Questo può essere trovato calcolando la radice quadrata della varianza. Il quadrato di 0,0074 s = 0,09 s, quindi la deviazione standard è 0,09 s.

5. Fornire il valore misurato finale. Lo fai annotando la media dei valori misurati insieme alla deviazione standard aggiunta e sottratta. Poiché la media delle letture è 0,42 s e la deviazione standard è 0,09 s, la lettura finale è 0,42 s ± 0,09 s.
Metodo 3 di 3: Operazioni aritmetiche con imprecisione

1. Aggiunta imprecisione. Lo fai sommando le letture e aggiungendo le loro imprecisioni:
- (5 cm ± .2 cm) + (3 cm ± .1 cm) =
- (5 cm + 3 cm) ± (.2 cm +. 1 cm) =
- 8 cm ± .3 cm

2. Sottraendo l`imprecisione. Lo fai sottraendo i valori misurati e sommando le imprecisioni:
3. Moltiplicando l`imprecisione.
Per moltiplicare l`imprecisione, moltiplicare le misurazioni e aggiungere l`imprecisione RELATIVA (in percentuale):
Il calcolo delle imprecisioni attraverso la moltiplicazione non funziona con valori assoluti (come con addizione e sottrazione), ma con valori relativi. Si ottiene l`imprecisione relativa dividendo l`imprecisione assoluta per il valore misurato, quindi moltiplicandolo per 100.
Ad esempio:
Per moltiplicare l`imprecisione, moltiplicare le misurazioni e aggiungere l`imprecisione RELATIVA (in percentuale):
Il calcolo delle imprecisioni attraverso la moltiplicazione non funziona con valori assoluti (come con addizione e sottrazione), ma con valori relativi. Si ottiene l`imprecisione relativa dividendo l`imprecisione assoluta per il valore misurato, quindi moltiplicandolo per 100.
Ad esempio:
Così:
4. Condivisione dell`imprecisione.
Per dividere l`imprecisione, dividere le misure e aggiungere l`imprecisione RELATIVA:
Questa procedura equivale a una moltiplicazione!
Per dividere l`imprecisione, dividere le misure e aggiungere l`imprecisione RELATIVA:
Questa procedura equivale a una moltiplicazione!

5. Aumentare esponenzialmente una lettura imprecisa. Per aumentare esponenzialmente una misurazione imprecisa, aumentare la misurazione di una certa potenza, quindi moltiplicare l`imprecisione per quella potenza:
Consigli
- È possibile visualizzare i risultati e l`imprecisione predefinita nel loro insieme o per ciascun risultato all`interno di un insieme di dati. Una regola generale è che i dati ottenuti da misurazioni multiple sono meno accurati di quelli ottenuti direttamente da una misurazione individuale.
Avvertenze
- L`imprecisione qui descritta è applicabile solo ai casi in cui vengono utilizzate statistiche normali (gaussiane, a forma di campana). Altri spread richiedono un metodo diverso per descrivere l`imprecisione.
- Una buona ricerca non finisce mai "fatti" o cosa "vero" è. Sebbene sia molto probabile che una misurazione rientri in un certo intervallo di imprecisione, non vi è alcuna garanzia che lo farà. È inerente ai valori misurati scientifici che esiste la possibilità che i valori misurati non siano corretti.
Articoli sull'argomento "Calcola imprecisione"
Condividi sui social network:
Popolare