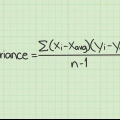Calcolo dell'Intervallo: 4 Passaggi (con Immagini)

Contenuto

Passi
Consigli

L `"intervallo" nella statistica rappresenta la differenza tra i valori più alti e più bassi in un set di dati. L`intervallo mostra quanto sono distribuiti i valori in una serie. Se l`intervallo è ampio, i valori della serie sono molto distanti; se l`intervallo è piccolo, i valori sono vicini l`uno all`altro. Se vuoi sapere come calcolare la larghezza dello spread, tutto ciò che devi fare è seguire questi passaggi.

Passi

Immagine titolata Calculate Range Step 1

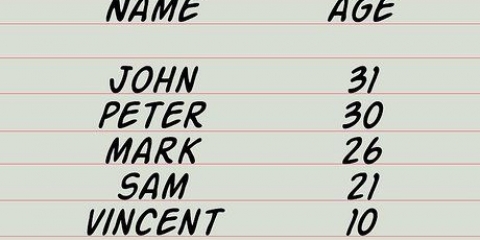
1. Elenca gli elementi nel tuo set di dati. Per trovare l`intervallo di un set devi allineare tutti gli elementi del set in modo da poter trovare i numeri più alti e più bassi. Annota tutti gli elementi. I numeri in questo set sono: 14, 19, 20, 24, 25 e 28.

È più facile trovare i numeri più alti e più bassi nell`insieme se metti i numeri in ordine crescente. In questo esempio, il set è ordinato come segue: 14, 19, 20, 24, 24, 25, 28.
L`organizzazione del set di dati può anche aiutarti a eseguire altri calcoli, come trovare la modalità, la media o la mediana del set.

Immagine titolata Calculate Range Step 2

2. Trova i numeri più alti e più bassi nell`insieme. In questo caso, il numero più basso del set è 14 e il numero più alto è 28.

Immagine titolata Calculate Range Step 3

3. Sottrai il numero più piccolo nel tuo set di dati dal numero più grande. Ora che hai trovato il numero più piccolo e quello più grande nell`insieme, tutto ciò che devi fare è sottrarli. Sottrarre 14 da 28 (28 - 14) e ottieni 14, la larghezza di diffusione del set.

Immagine titolata Calculate Range Step 4

4. Etichetta la larghezza di diffusione. Una volta trovato lo spread, etichettalo chiaramente. Ciò evita confusione con qualsiasi altro calcolo statistico che potrebbe essere necessario eseguire per l`insieme, come trovare la mediana, la modalità o la media.

Consigli

La mediana di un set di dati statistico rappresenta la "metà" del set di dati in termini di distribuzione e non l`intervallo dei dati. Quindi, mentre si è tentati di presumere che la mediana di un dato set di dati sia l`intervallo diviso per 2, o a metà strada tra gli estremi dell`intervallo, di solito non è così. Per trovare la mediana corretta devi prima mettere in ordine gli elementi dei dati, quindi trovare l`elemento al centro dell`elenco. Quell`elemento è la mediana. Ad esempio, se hai una lista con 29 elementi, il 15° elemento è equidistante sia dalla cima che dalla fine della lista ordinata. Quindi il 15° elemento è la mediana, indipendentemente da come quel valore sia correlato all`intervallo.
Puoi anche capire `diffusione` in un contesto algebrico, dove di solito è chiamato `intervallo`. Per capirlo devi prima farti un`idea del concetto di funzione algebrica, o sequenza di operazioni su un dato numero. Poiché le operazioni della funzione possono essere eseguite su qualsiasi numero, anche un numero sconosciuto, il numero è rappresentato da una variabile lettera, solitamente "x". Il dominio è l`insieme di tutti i possibili valori di input che puoi sostituire con questo numero sconosciuto. Lo scopo della funzione è l`insieme di tutti i possibili risultati che puoi ottenere se inserisci uno dei valori di dominio ed esegui tutte le operazioni della funzione. Sfortunatamente, non esiste un modo per calcolare l`intervallo di una funzione. A volte rappresentare graficamente la funzione o calcolare più valori può mostrare uno schema chiaro. Puoi anche utilizzare ciò che sai sul dominio della funzione per escludere possibili valori di output o per limitare il set di dati che indica l`ambito.