Nel nostro esempio prendiamo le radici quadrate di 25 e 16. Vedi sotto: Sqrt(25×16) Sqrt(25) × Sqrt(16) 5 × 4 = 20 
Prendiamo come esempio la radice quadrata di 147. 147 non è il prodotto di due quadrati perfetti, quindi non possiamo ottenere un bel valore intero. Ma è il prodotto di un quadrato perfetto e di un altro numero: 49 e 3. Possiamo usare queste informazioni per scrivere la nostra risposta nei termini più semplici: quadrato(147) = Sqrt(49 × 3) = Sqrt(49) × Sqrt(3) = 7 × mq(3) 
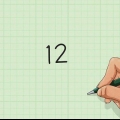
Torniamo al nostro esempio. Poiché 2 = 4 e 1 = 1, sappiamo che Sqrt(3) è compreso tra 1 e 2 – probabilmente più vicino a 2 che a 1. Stimiamo che 1.7. 7 × 1,7 = 11.9. Controllando questo con la calcolatrice, vediamo che siamo abbastanza vicini alla risposta: 12.13. Questo funziona anche per i numeri più grandi. Ad esempio, Sqrt(35) è all`incirca tra 5 e 6 (probabilmente più vicino a 6). 5 = 25 e 6 = 36. 35 è compreso tra 25 e 36, quindi la radice quadrata sarà compresa tra 5 e 6. Poiché 35 è appena sotto 36, possiamo dire con una certa sicurezza che la sua radice quadrata appena è inferiore a 6. Il controllo con una calcolatrice ci dà una risposta di circa 5,92 - avevamo ragione. 
Un esempio: determiniamo la radice quadrata di 45 usando questo metodo. Sappiamo che 45 = 9 × 5 e che 9 = 3 × 3. Quindi possiamo scrivere la radice quadrata in questo modo: Sqrt(3 × 3 × 5). Basta rimuovere i 3 e posizionare un 3 al di fuori del radicale per ottenere una radice quadrata semplificata: (3)Sqrt(5). Ora puoi facilmente stimare. Un ultimo esempio; determiniamo la radice quadrata di 88: quadrato(88) = Sqrt(2 × 44) = Sqrt(2 × 4 × 11) = Sqrt(2 × 2 × 2 × 11). Abbiamo diversi 2 nella nostra radice quadrata. Poiché 2 è primo, possiamo rimuovere una coppia e posizionare un 2 fuori dalla radice quadrata. = La nostra radice quadrata nei termini più semplici è (2) Sqrt(2 × 11) o (2) Sqrt(2) Sqrt(11). Ora possiamo avvicinarci a Sqrt(2) e Sqrt(11) e trovare una risposta stimata, se volessimo. 

Nel nostro esempio, la cifra più a sinistra è il numero 7. Perché sappiamo che 2 = 4 7 < 3 = 9, possiamo dire che n = 2 perché è l`intero più grande il cui quadrato è minore o uguale a 7. Scrivi 2 nel quadrante in alto a destra. Questa è la prima cifra della risposta. Scrivi 4 (il quadrato di 2) nel quadrante in basso a destra. Questo numero è importante per il passaggio successivo. 
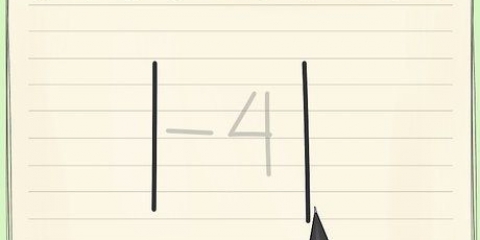
Nel nostro esempio, scriviamo un 4 sotto 7 e lo sottraiamo. Questo da 3 come risposta. 
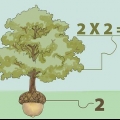
Nel nostro esempio, il seguente numero è "80". Nota "80" accanto al 3 nel quadrante sinistro. Quindi moltiplica il numero in alto a destra per 2. Questo numero è 2, quindi 2 × 2 = 4. Nota "`4"` in basso a destra, seguito da _×_=. 
Nel nostro esempio, riempiamo 8, e questo dà 4(8) × 8 = 48 × 8 = 384. Questo è maggiore di 380. Quindi 8 è troppo grande, ma 7 probabilmente non lo è. Inserisci 7 e risolvi: 4(7) × 7 = 329. 7 va bene perché 329 è minore di 380. Nota 7 in alto a destra. Questa è la seconda cifra nella radice quadrata di 780,14. 
Nel nostro esempio, sottraiamo 329 da 380 e questo dà 51 come risultato. 
Nella nostra risposta ora scriviamo una virgola perché lo incontriamo anche in 780.14. Sposta la coppia successiva (14) in basso nel quadrante sinistro. 27 x 2 = 54, quindi scriviamo "54 _×_=" nel quadrante in basso a destra. 
Nel nostro esempio, 549 × 9 = 4941, che è minore o uguale al numero a sinistra (5114). 549 × 10 = 5490, che è troppo alto, quindi 9 è la nostra risposta. Scrivi 9 come numero successivo in alto a destra e sottrai il risultato della moltiplicazione dal numero di sinistra: 5114 -4941 = 173. 
Calcola la radice quadrata di un numero senza calcolatrice
Contenuto
Prima dell`avvento delle calcolatrici, sia gli studenti che i professori dovevano calcolare le radici quadrate con carta e penna. All`epoca sono state sviluppate varie tecniche per affrontare questo compito a volte pesante, con alcune che forniscono una stima approssimativa e altre che calcolano il valore esatto. Continua a leggere per scoprire come trovare la radice quadrata di un numero in pochi semplici passaggi.
Passi
Metodo 1 di 2: Rooting con fattori primi

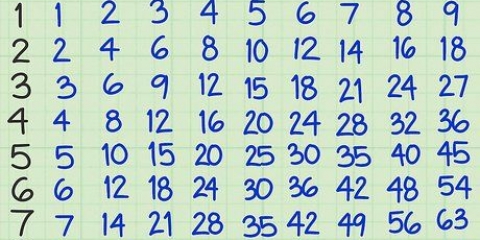
1. Dividi il tuo numero in quadrati. Questo metodo utilizza i fattori di un numero per trovare la radice quadrata di un numero (a seconda del numero, questa può essere una risposta esatta o una stima). Il fattori di un dato numero sono una sequenza casuale di numeri moltiplicati insieme per formare quel particolare numero. Ad esempio, puoi dire che i fattori di 8 sono uguali a 2 e 4 perché 2 × 4 = 8. I quadrati perfetti, d`altra parte, sono interi che sono il prodotto di altri interi. Ad esempio: 25, 36 e 49 sono quadrati perfetti perché sono rispettivamente pari a 5, 6 e 7. I secondi fattori di potenza sono, come avrai capito, fattori che sono anche quadrati perfetti. Per trovare una radice quadrata usando i fattori primi, prova prima a dividere il numero nei suoi fattori cubici.
- Prendi il seguente esempio. Troviamo la radice quadrata di 400. Per cominciare, dividiamo il numero in quadrati. Poiché 400 è un multiplo di 100, sappiamo che è equamente divisibile per 25: un quadrato perfetto. La memorizzazione rapida ci dice che 400 / 25 = 16. 16 sembra anche essere un quadrato perfetto. Quindi lo sono i fattori quadratici di 400 25 e 16 perché 25 × 16 = 400.
- Scriviamo questo come: Sqrt(400) = Sqrt(25 × 16)

2. Prendi le radici quadrate delle tue radici quadrate. La regola del prodotto delle radici quadrate afferma che per un dato numero un e B, Sqrt(a × b) = Sqrt(a) × Sqrt(b). A causa di questa proprietà, ora possiamo prendere le radici quadrate dei fattori del cubo e moltiplicarle insieme per la risposta.

3. Se il tuo numero non può essere scomposto perfettamente, semplificalo. In realtà, i numeri di cui vuoi trovare le radici quadrate non saranno bei numeri arrotondati con belle radici quadrate come 400. In questi casi potrebbe non essere possibile ottenere un numero intero come risposta. Invece, usando tutti i cubi che riesci a trovare, puoi determinare la risposta come una radice quadrata più piccola e più facile da usare. Puoi farlo riducendo il numero a una combinazione di fattori cubo e altri fattori, quindi semplificandolo.

4. Semplificare, se necessario. Usando la radice quadrata nei termini più semplici, di solito è abbastanza facile ottenere una stima approssimativa della risposta stimando le radici quadrate rimanenti e moltiplicandole. Un modo per migliorare le tue ipotesi è trovare i quadrati perfetti su entrambi i lati del numero nella radice quadrata. Sai che il valore decimale del numero nella tua radice quadrata è da qualche parte tra questi due numeri, quindi anche la tua ipotesi dovrebbe essere compresa tra questi numeri.

5. In alternativa, come primo passo, puoi semplificare il numero inminimo comune multiplo. La ricerca dei fattori quadrati non è necessaria se si trovano facilmente i fattori primi di un numero (fattori che sono anche primi contemporaneamente). Scrivi il numero in termini di multipli minimi comuni. Quindi cerca tra i tuoi fattori le corrispondenti coppie di numeri primi. Se trovi due fattori primi che corrispondono, rimuovili dalla radice quadrata e mettili un di questi numeri al di fuori del radicale.
Metodo 2 di 2: Trovare radici quadrate senza calcolatrice
Con una lunga divisione

1. Dividi le cifre del tuo numero in coppie. Questo metodo è simile alla divisione lunga, che ti consente di farlo esatto trova la radice quadrata di un numero cifra per cifra. Sebbene non sia essenziale, dividere un numero in blocchi praticabili può renderlo più facile da risolvere, soprattutto se è lungo. Per prima cosa traccia una linea verticale che divide l`area di lavoro in 2 aree, quindi una linea più corta vicino alla parte superiore dell`area destra, dividendola in una parte superiore più piccola e una parte più grande in basso. Quindi dividi il numero in coppie di numeri, partendo dal punto decimale. Secondo questa regola, 79520789182.47897 diventa uguale a "7 95 20 78 91 82,47 89 70". Scrivi questo numero nell`area in alto a sinistra.
- Ad esempio, calcoliamo la radice quadrata di 780,14. Dividi il tuo spazio di lavoro come indicato sopra e scrivi "7 80, 14" nell`angolo in alto a sinistra. Va bene se c`è solo un numero all`estrema sinistra, invece di due. Quindi scrivi la risposta (la radice quadrata di 780,14) nella parte superiore dell`area a destra.

2. Trova il numero intero più grande n il cui quadrato è minore o uguale alla cifra o numero più a sinistra. Trova il quadrato più grande minore o uguale a questo numero, quindi trova la radice quadrata di questo quadrato. Questo numero è n. Nota che nell`area in alto a destra e scrivi il quadrato di n nel quadrante inferiore di quell`area.

3. Sottrai il numero che hai calcolato della cifra o del numero più a sinistra. Come per la divisione lunga, il passaggio successivo consiste nel sottrarre il quadrato dal numero che abbiamo appena usato per calcolare. Scrivi questo numero sotto il numero più a sinistra e sottraili l`uno dall`altro. Scrivi la risposta qui sotto.

4. Sposta il numero successivo verso il basso. Posizionalo accanto al valore che hai trovato nella modifica precedente. Moltiplica il numero in alto a destra per due e scrivilo in basso a destra. Risparmia spazio accanto al numero che hai appena annotato per la somma della moltiplicazione che farai nel passaggio successivo. Scrivere qui `"_×_="`.

5. Inserisci i numeri a destra. Nello spazio vuoto della somma (a destra), inserisci il numero intero più grande che renderà il risultato della moltiplicazione a destra minore o uguale al numero corrente a sinistra.

6. Sottrarre il numero appena calcolato dal numero corrente a sinistra. Quindi sottrai il risultato della moltiplicazione a destra dalla risposta corrente a sinistra. Scrivi la tua risposta direttamente qui sotto.

7. Ripetere il passaggio 4. Sposta la coppia di numeri successiva da 780,14 verso il basso. Se arrivi a una virgola, scrivi quella virgola nella risposta a destra. Quindi moltiplica per 2 il numero in alto a destra e scrivi la risposta accanto a ("_ × _") come sopra.

8. Ripetere i passaggi 5 e 6. Trova il numero più grande che fornisce una risposta minore o uguale al numero corrente a sinistra. Risolvere.

9. Per rendere accurato il risultato, ripeti la procedura precedente fino a trovare la risposta con il numero di decimali (centesimi, millesimi) di cui hai bisogno.
Comprendere la procedura
- Nota che se dividi 88962 per 7 usando la divisione lunga, il primo passaggio è lo stesso: hai a che fare con la prima cifra di 88962 (8) e vuoi che la cifra più grande moltiplicata per 7 sia minore o uguale a 8. In sostanza decidi tu D in modo che 7×d ≤ 8 < 7×(d+1). In questo caso d è uguale a 1.
- Nel nostro esempio (10A+B)² = L = S = 100A² + 2×10A×B + B². Ricorda che 10A+B rappresenta la nostra risposta L insieme a B nella posizione delle unità e A nella posizione delle decine. Ad esempio, se A=1 e B=2, allora 10A+B è il numero 12. (10A+B)² è l`area dell`intera piazza, mentre 100 A² è l`area della piazza interna più grande, B² è l`area del minimo quadrato e 10A×B è l`area di ciascuno dei restanti rettangoli. Attraverso questo lungo e complicato procedimento, possiamo trovare l`area dell`intero quadrato sommando le aree dei quadrati e dei rettangoli che lo compongono.

1. Considera il numero di cui vuoi calcolare la radice quadrata come area S di un quadrato. Poiché l`area di un quadrato è L, dove L è la lunghezza di uno dei suoi lati, quindi prendendo la radice quadrata del tuo numero, provi a calcolare la lunghezza L del lato di quel quadrato.

2. Assegna una lettera a ogni cifra della tua risposta. Assegna la variabile A come prima cifra di L (la radice quadrata che stiamo cercando di calcolare). B è la seconda cifra, C è la terza e così via.

3. Date una lettera a ciascuno "coppia di numeri" del numero con cui inizi. Dare la variabile Sun alla prima coppia di cifre in S (il valore iniziale), SB alla seconda coppia di cifre, ecc.

4. Comprendere la relazione tra questo metodo e la lunga divisione. Questo metodo per trovare una radice quadrata è essenzialmente una divisione lunga, dividendo il valore iniziale per la sua radice quadrata e prendendo la radice quadrata come risposta "dato". Come con la divisione lunga, dove sei interessato solo alla cifra successiva alla volta, sei interessato solo alle due cifre successive alla volta (che corrispondono alla cifra successiva della radice quadrata).

5. Trova il numero più grande il cui quadrato è minore o uguale a Sun è. La prima cifra A nella nostra risposta è quindi l`intero più grande il cui quadrato non è maggiore di Sun (A tale che A² ≤ Sa < (LA+1)²). Nel nostro esempio, S. èun = 7 e 2² ≤ 7 < 3², quindi A = 2.

6. Visualizza il quadrato di cui vuoi trovare l`area. La tua risposta, la radice quadrata del valore iniziale, è L, che descrive la lunghezza di un quadrato di area S (il valore iniziale). I valori per A, B e C rappresentano i numeri nel valore L. Un altro modo per dirlo è che per una risposta a 2 cifre, 10A + B = L, e per una risposta a 3 cifre, 100A +10B + C = L, e così via.

7. Sottrarre A² da Sun. Porta una coppia di numeri (SB) dal numero S. Sun SB è la superficie quasi totale della piazza, dalla quale hai appena sottratto l`area della piazza interna più grande. Il resto è diciamo il numero N1, che abbiamo ottenuto nel passaggio 4 (N1 = 380 nel nostro esempio). N1 è uguale a 2×10A×B + B² (l`area dei 2 rettangoli più l`area del quadratino).

8. Guarda N1 = 2×10A×B + B², scritto anche come N1 = (2×10A + B) × B. Nel nostro esempio conosci già N1 (380) e A (2), quindi ora devi trovare B. B probabilmente non è un numero intero, quindi è necessario in realtà trova l`intero più grande B, tale che (2×10A + B) × B ≤ N1. Quindi ora hai: N1 < (2×10A + (B+1)) × (B+1).)

9. Risolvi l`equazione. Per risolvere questa equazione, moltiplica A per 2, spostalo alle decine (moltiplica per 10), posiziona B nelle unità e moltiplica il risultato per B. In altre parole, (2×10A + B) × B. Questo è esattamente quello che fai quando scrivi "N_×_=" (con N=2×A) nel quadrante in basso a destra al punto 4. Nel passaggio 5 si determina l`intero più grande B che si adatta al di sotto della linea, tale che (2×10A + B) × B ≤ N1.

10. Sottrarre l`area (2×10A + B) × B dall`area totale. Questo produce l`area S-(10A+B)² che non hai ancora preso in considerazione (e che usi per calcolare i seguenti numeri allo stesso modo).

11. Per calcolare la cifra successiva C, ripetere la procedura. Sposta la coppia di numeri successiva da S in basso (SC) per ottenere N2 a sinistra e cercare il C più grande in modo da avere: (2×10×(10A+B)+C) × C ≤ N2 (uguale al doppio del numero a due cifre "A B" seguito da "_×_=" . Ora determina il numero più grande che puoi inserire qui, che ti darà una risposta inferiore o uguale a N2.
Consigli
- Spostando la virgola decimale di due posizioni (un fattore 100) si sposta la virgola decimale nella radice quadrata corrispondente di una posizione (un fattore 10).
- Nell`esempio, 1.73 può essere considerato come "riposo": 780,14 = 27,9² + 1,73.
- Questo metodo funziona per qualsiasi sistema numerico, non solo per il sistema decimale (dieci decimali).
- Sentiti libero di mettere i calcoli dove vuoi. Alcune persone lo scrivono sopra il numero di cui vogliono calcolare la radice quadrata.
- Un metodo alternativo è il seguente: √z = √(x^2+y) = x + y/(2x + y/(2x + y/(2x + ...))). Ad esempio, per calcolare la radice quadrata di 780,14, dovresti prendere l`intero al quadrato più vicino a 780,14 (28), quindi =780,14, x=28 e y=-3,86. La compilazione e la stima ci danno x + y/(2x) e questo dà (termini semplificati) 78207/2800 o circa 27,931(1); il termine successivo, 4374188/156607 o circa 27.930986(5). Ogni termine aggiunge circa 3 decimali di precisione al precedente.
Avvertenze
- Assicurati di dividere il numero in coppie partendo dal punto decimale. Dividendo 79520789182.47897 come "79 52 07 89 18 2.4 78 97" dà un risultato non corretto.
Articoli sull'argomento "Calcola la radice quadrata di un numero senza calcolatrice"
Condividi sui social network:
Simile
Popolare