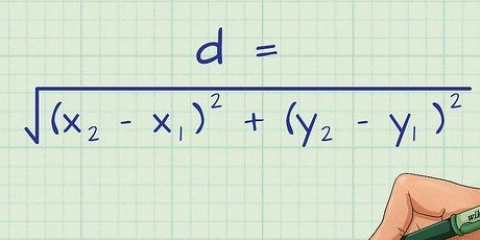Calcolo del Valore Assoluto di un Numero: 15 Passaggi (con Immagini)

Contenuto

Passi
- Metodo 1 di 2: Determina il valore assoluto
- Metodo 2 di 2: risoluzione di equazioni complesse con valori assoluti (equazioni con `i`)
Consigli

Il valore assoluto di un numero è facile da trovare e la teoria alla base è importante per risolvere equazioni con un valore assoluto. Ogni valore assoluto è una misura di quanto quel numero è lontano da zero. Se pensi a una linea numerica, con lo zero al centro, puoi scoprire quanto è lontano il numero in questione da quello zero.

Passi

Metodo 1 di 2: Determina il valore assoluto

Immagine titolata Trova il valore assoluto di un numero Passaggio 1

1. Ricorda che il valore assoluto è la distanza di un numero da zero. Un valore assoluto è la distanza dal numero a zero lungo una linea numerica. o,

| - 4 |

${displaystyle |-4|}$ quindi indica semplicemente quanto è lontano -4 da zero. Poiché la distanza è sempre un numero di posizione (non ci si può muovere a passi `negativi`, solo in una direzione diversa), il risultato del valore assoluto è sempre positivo.

Immagine titolata Trova il valore assoluto di un numero Passaggio 2

2. Rendi positivo il numero all`interno delle barre del valore assoluto. In poche parole, il valore assoluto rende positivo qualsiasi numero. È utile per misurare la distanza, o determinare valori in materia finanziaria, lavorando con numeri negativi come debiti o prestiti.

Immagine titolata Trova il valore assoluto di un numero Step 3

3. Utilizzare semplici barre verticali per indicare un valore assoluto. Il formato per un valore assoluto è facile. Righe singole (che si trovano vicino al tasto Invio su una tastiera) attorno a un numero o un`espressione, ad esempio

| n |, | 3 + 5 |, | - 72 |

${displaystyle |n|,|3+5|,|-72|}$ , indica un valore assoluto.

| 2 |

${displaystyle |2|}$ è `il valore assoluto di 2.`

Immagine titolata Trova il valore assoluto di un numero Step 4

4. Ometti i segni meno per il numero all`interno dei segni di valore assoluto. Ad esempio: |-5| quindi diventa |5|.

Immagine titolata Trova il valore assoluto di un numero Passaggio 5

5. Ometti i segni di valore assoluto. Il numero che rimane è la risposta, quindi |-5| diventa |5| e poi 5. Quanto segue è tutto ciò che devi fare:

| - 5 | = 5

${displaystyle |-5|=5}$

Immagine titolata Trova il valore assoluto di un numero Passaggio 6

6. Semplifica l`espressione entro il valore assoluto. È un`espressione semplice, come

| - 10 |

${displaystyle |-10|}$ , quindi puoi semplicemente renderlo positivo. Ma un`espressione come

| (- 4 * 5) + 3 - 2 |

${displaystyle |(-4*5)+3-2|}$ deve essere semplificato prima di poterne trovare il valore assoluto. L`ordine fisso delle operazioni resta valido:

Incarico:

| (- 4 * 5) + 3 - 2 |

${displaystyle |(-4*5)+3-2|}$

Semplifica tra parentesi:

| (- 20) + 3 - 2 |

${displaystyle |(-20)+3-2|}$

Somma e sottrai:

| - 19 |

${displaystyle |-19|}$

Rendi positivo tutto ciò che rientra nel valore assoluto:

| 19 |

${displaystyle |19|}$

Risposta finale: 19

Immagine titolata Trova il valore assoluto di un numero Passaggio 7

7. Utilizzare sempre questo ordine di operazioni prima di calcolare il valore assoluto. Quando si elaborano equazioni più lunghe, si esegue tutto il lavoro necessario prima di determinare il valore assoluto. Non cercare di semplificare i valori assoluti finché tutto non viene sommato, sottratto e diviso correttamente. Ad esempio:

Incarico:

1 + 2 + | 4 - 7 | 5 * | - 3 * 2 |

${displaystyle {frac {1+2+|4-7|}{5*|-3*2|}}}$

Esegui l`ordine delle operazioni all`interno e all`esterno del valore assoluto:

3 + | - 3 | 5 * | - 6 |

${displaystyle {frac {3+|-3|}{5*|-6|}}}$

Determina i valori assoluti:

3 + (3) 5 * (6)

${displaystyle {frac {3+(3)}{5*(6)}}}$

Ordine delle operazioni:

\frac{6}{30}

${displaystyle {frac {6}{30}}}$

Semplifica la risposta finale: $\frac{1}{5}$ ${frac{1}{5}}$

Immagine titolata Trova il valore assoluto di un numero Step 8

8. Continua a lavorare su alcuni esercizi di esempio per prenderne il controllo. Calcolare il valore assoluto di un numero è molto semplice, ma ciò non significa che fare problemi di pratica non sarebbe utile per rispolverare le tue conoscenze:

| 12 |

${displaystyle |12|}$ =

12

${ displaystyle 12}$

| - 24 |

${displaystyle |-24|}$ =

24

${ displaystyle 24}$

| 3 + 2 - 11 + 5 - 6 |

${displaystyle |3+2-11+5-6|}$ =

7

$7$

Metodo 2 di 2: risoluzione di equazioni complesse con valori assoluti (equazioni con `i`)

Immagine titolata Trova il valore assoluto di un numero Step 9

1. Fai attenzione quando hai a che fare con equazioni complesse che coinvolgono numeri immaginari, come `i` o -1{displaystyle {sqrt {-1}}} ${displaystyle {sqrt {-1}}}$ , e risolverli separatamente. Non puoi trovare il valore assoluto dei numeri immaginari nello stesso modo in cui puoi trovare i numeri razionali. Puoi trovare il valore assoluto di un`equazione complessa elaborandolo nella formula della distanza. Prendi l`espressione

| 3 - 4 io |

${displaystyle |3-4i|}$ come esempio.

Incarico: $| 3 - 4 io |$ ${displaystyle |3-4i|}$
Fai attenzione: Se usi un`espressione come $\sqrt{- 1}$ ${displaystyle {sqrt {-1}}}$ puoi sostituirlo con `i.` La radice quadrata di -1 è un numero immaginario, i. $| io | = 1$ ${displaystyle |i|=1}$

Immagine titolata Trova il valore assoluto di un numero Step 10

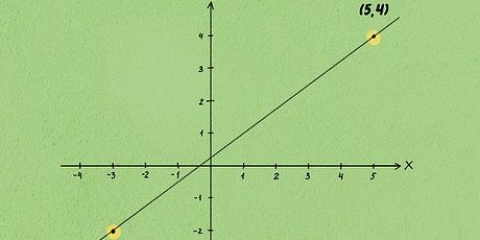
2. Trova i coefficienti dell`equazione complessa. Prendi 3-4i come equazione di una retta. Il valore assoluto è la distanza da zero, quindi determini la distanza da zero per il punto (3, -4) su questa linea.I coefficienti sono semplicemente i due numeri che non sono `i`. Sebbene il numero accanto alla i sia solitamente il secondo numero, non importa quando si risolve. Esercitati con i seguenti coefficienti:

| 1 + 6 io |

${displaystyle |1+6i|}$ = (1, 6)

| 2 - io |

${displaystyle |2-i|}$ = (2, -1)

| 6 io - 8 |

${displaystyle |6i-8|}$ = (-8, 6)

Immagine titolata Trova il valore assoluto di un numero Step 11

3. Rimuovere i simboli del valore assoluto dall`equazione. Ora ti servono solo i coefficienti. Ricorda che determini la distanza dell`equazione da zero. Poiché nel passaggio successivo utilizzerai la formula della distanza, questo equivale a determinare il valore assoluto.

Immagine titolata Trova il valore assoluto di un numero Step 12

4. Al quadrato entrambi i coefficienti. Per determinare la distanza, si utilizza la formula della distanza, nota anche come

\sqrt{X} 2 + y^{2}

${displaystyle {sqrt {x^{2}+y^{2}}}}$ . Quindi, come primo passo, devi quadrare entrambi i coefficienti dell`equazione complessa. Continuiamo con l`esempio:

| 3 - 4 io |

${displaystyle |3-4i|}$ :

Coefficienti: (3, -4)

Formula distanza:

\sqrt{3} 2 + (- 4)^{2}

${displaystyle {sqrt {3^{2}+(-4)^{2}}}}$

Al quadrato i coefficienti: `

\sqrt{9 + 16}

${displaystyle {sqrt {9+16}}}$

Fai attenzione: Esercitati di nuovo con la formula della distanza se non la capisci. Nota che la quadratura di entrambi i numeri li rende positivi, dandoti essenzialmente il valore assoluto.

Immagine titolata Trova il valore assoluto di un numero Step 13

5. Metti il prodotto dei numeri sotto il radicale. Il segno radicale indica che stai sottraendo la radice quadrata del numero sottostante. Ora somma prima i numeri, senza fare nulla per il segno radicale.

Coefficienti: (3, -4)

Formula distanza:

\sqrt{3} 2 + (- 4)^{2}

${displaystyle {sqrt {3^{2}+(-4)^{2}}}}$

Al quadrato i coefficienti:

\sqrt{9 + 16}

${displaystyle {sqrt {9+16}}}$

Somma il prodotto dei coefficienti:

\sqrt{25}

${displaystyle {sqrt {25}}}$

Immagine titolata Trova il valore assoluto di un numero Step 14

6. Prendi la radice quadrata per la tua risposta finale. Devi solo semplificare l`equazione per la risposta finale. Questa è la distanza dal tuo "punto" su una linea numerica immaginaria al punto zero. Se non c`è radice quadrata, lascia la risposta dell`ultimo passaggio sotto il segno radicale: questa è una risposta corretta.

Coefficienti: (3, -4)

Formula distanza:

\sqrt{3} 2 + (- 4)^{2}

${displaystyle {sqrt {3^{2}+(-4)^{2}}}}$

Al quadrato i coefficienti:

\sqrt{9 + 16}

${displaystyle {sqrt {9+16}}}$

Somma il prodotto dei coefficienti:

\sqrt{25}

${displaystyle {sqrt {25}}}$

Sottrarre la radice quadrata per la risposta finale: 5

$| 3 - 4 io | = 5$ ${displaystyle |3-4i|=5}$

Immagine titolata Trova il valore assoluto di un numero Step 15

7. Prova alcuni esercizi pratici. Clicca con il mouse direttamente dietro le domande per vedere le risposte, in bianco.

| 1 + 6 io |

${displaystyle |1+6i|}$ = √37

| 2 - io |

${displaystyle |2-i|}$ = √5

| 6 io - 8 |

${displaystyle |6i-8|}$ = 10

Consigli

Se hai una variabile all`interno di un valore assoluto, non puoi rimuovere i segni di valore assoluto usando questo metodo, perché se il valore della variabile è negativo, il valore assoluto lo renderebbe positivo.
Se hai un`espressione all`interno di un valore assoluto, semplifica l`espressione prima di determinarne il valore assoluto.
Quando un numero positivo è all`interno degli indicatori di valore assoluto, la risposta è sempre quel numero.
È necessario un metodo diverso per risolvere le equazioni del valore assoluto con x e y, sebbene la teoria alla base del valore assoluto sia utilizzata come base.
Un valore assoluto non può mai essere un numero negativo, quindi se vedi qualcosa come | 2 - 4x| = -7, allora sai che questa equazione è falsa senza doverla risolvere.