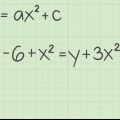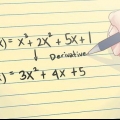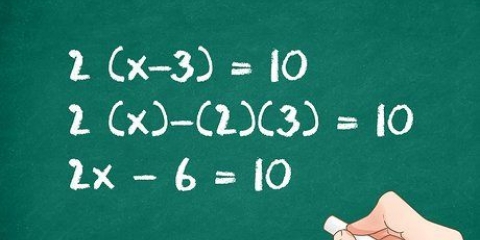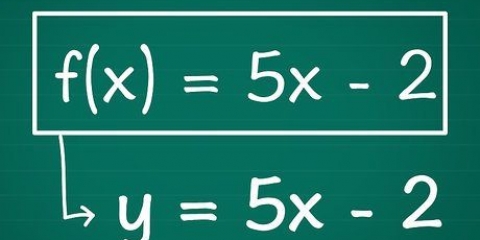Trovare il Valore Estremo di un'Equazione: 10 Passaggi (con Immagini)

Contenuto

Passi
- Metodo 1 di 2: La formula x = -b/2a
- Metodo 2 di 2: elaborare l`equazione
Consigli
Avvertenze
Necessità

Il valore estremo di una parabola è il massimo o il minimo dell`equazione. Se vuoi trovare il valore estremo di un`equazione quadratica, usa una formula o risolvi l`equazione. Qui imparerai come farlo.

Passi

Metodo 1 di 2: La formula x = -b/2a

Immagine titolata Trova il vertice di un`equazione quadratica Passaggio 1

1. Determina i valori di a, b e c. In un`equazione quadratica o quadratica,X = un,X = b, e la costante (il termine senza variabile) = C. Supponiamo di avere a che fare con la seguente equazione: y = x + 9 x + 18. In questo esempio, un = 1, B = 9 e C = 18.

Immagine titolata Trova il vertice di un`equazione quadratica Passaggio 2

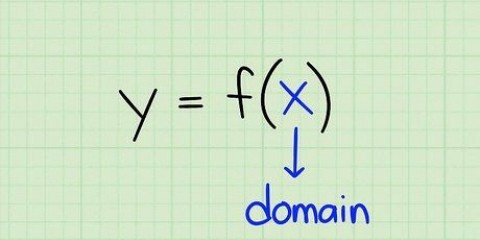
2. Usa una formula per trovare il valore di x. Il vertice della parabola è anche l`asse di simmetria dell`equazione. La formula per trovare il valore estremo x di un`equazione quadratica è x = -b/2a. Compila i valori rilevanti in questa equazione per ottenere X trovare. Sostituisci i valori per a e b. Ecco come:

x=-b/2a

x=-(9)/(2)(1)

x=-9/2

Immagine titolata Trova il vertice di un`equazione quadratica Passaggio 3

3. Inserisci il valore di x nell`equazione originale per ottenere il valore di y. Ora che conosci x è possibile applicare questo valore all`equazione originale per ottenere y. La formula per determinare il valore estremo di un`equazione quadratica è (x, y) = [(-b/2a), f(-b/2a)]. Questo significa solo che per ottenere y, puoi trovare x usando questa formula e quindi inserirla nell`equazione originale. Ecco come va:

y = x + 9x + 18

y = (-9/2) + 9(-9/2) +18

y = 81/4 -81/2 + 18

y = 81/4 -162/4 + 72/4

y = (81 - 162 + 72)/4

y = -9/4

Immagine titolata Trova il vertice di un`equazione quadratica Passaggio 4

4. Scrivi i valori per xey come una coppia ordinata. Ora che sai che x = -9/2 e y = -9/4, scrivi questi valori come una coppia ordinata: (-9/2, -9/4). Il valore estremo di questa equazione quadratica è (-9/2, -9/4). Se vuoi disegnare questa parabola in un grafico, allora questo punto è il minimo della parabola, perché x è positivo.

Metodo 2 di 2: elaborare l`equazione

Immagine titolata Trova il vertice di un`equazione quadratica Passaggio 5

1. Scrivi l`equazione. Elaborare l`equazione è un altro modo per trovare il valore estremo di un`equazione quadratica. Con questo metodo è possibile trovare immediatamente le coordinate xey. Diciamo che stiamo lavorando con la seguente equazione quadratica: x + 4 x + 1 = 0.

Immagine titolata Trova il vertice di un`equazione quadratica Passaggio 6

2. Dividi ogni termine per il coefficiente di x . In questo caso, il coefficiente dix è uguale a 1, quindi puoi saltare questo passaggio. Dividere ogni termine per 1 non ha importanza!

Immagine titolata Trova il vertice di un`equazione quadratica Passaggio 7

3. Sposta la costante sul lato destro dell`equazione. La costante è il termine senza coefficiente. In questo caso è così "1". Sposta l`1 sull`altro lato dell`equazione sottraendo 1 da entrambi i lati. Ecco come farlo:

x + 4 x + 1 = 0

x + 4 x + 1 -1 = 0 - 1

x + 4 x = - 1

Immagine titolata Trova il vertice di un`equazione quadratica Passaggio 8

4. Completa il quadrato a sinistra dell`equazione.Opera (b/2) e aggiungi il risultato a entrambi i lati dell`equazione. riempire "4" come valore di B, perché "4x" il termine b è dell`equazione.

(4/2) = 2 = 4. Ora aggiungi 4 a entrambi i lati dell`equazione per ottenere quanto segue:

x + 4 x + 4 = -1 + 4

x + 4 x + 4 = 3

Immagine titolata Trova il vertice di un`equazione quadratica Passaggio 9

5. Fattorizzare il lato sinistro dell`equazione. Ora vedrai che x + 4x + 4 è un quadrato perfetto. Questo può essere riscritto come (x + 2) = 3

Immagine titolata Trova il vertice di un`equazione quadratica Passaggio 10

6. Usalo per trovare le coordinate xey. Puoi trovare la coordinata x semplicemente rendendo (x + 2) uguale a zero. Quindi se (x + 2) = 0, allora cosa dovrebbe essere x? La variabile x dovrebbe quindi essere uguale a -2 per compensare il +2, quindi la coordinata x è -2. La coordinata y è semplicemente il termine costante sull`altro lato dell`equazione. Quindi, y = 3. Puoi anche prendere una scorciatoia e prendere il segno del numero tra parentesi per trovare la coordinata x. Quindi, il valore estremo dell`equazione x + 4x + 1 = (-2, 3)

Consigli

Capire cosa rappresentano a, b e c.
Mostra il tuo lavoro e controllalo! Di conseguenza, il tuo insegnante sa che capisci e tu stesso hai la possibilità di vedere e correggere gli errori nelle tue risposte.
Rispettare questo ordine di elaborazione per garantire un buon esito dell`incarico.