Nota che ogni risultato è inferiore di $ 10 rispetto a quanto descritto sopra, poiché devi prima pagare $ 10 per partita, indipendentemente dal risultato. 
La tua calcolatrice 1/6 potrebbe fare qualcosa come 0,166667. Arrotondiamo questo valore a 0,167 per semplificare il calcolo, senza sacrificare la precisione. Se vuoi un risultato molto accurato, non convertirlo in decimale, inserisci semplicemente 1/6 nella formula e calcolalo in questo modo sulla tua calcolatrice. 
Non è necessario calcolare questi risultati ora, se si dispone di una calcolatrice in grado di eseguire più operazioni contemporaneamente. Otterrai un risultato più accurato se inserisci l`intera equazione. 

Più spesso una situazione viene ripetuta, più accuratamente il valore atteso è una rappresentazione del risultato medio effettivo. Ad esempio, potresti giocare 5 volte di seguito e perdere ogni volta, con una perdita media di 10 €. Tuttavia, se giochi altre 1000 volte, il risultato medio si avvicinerà sempre di più al valore atteso di -1,67 € a partita. Questo principio è chiamato "la legge dei grandi numeri." 

x = ___ 
x = (0,5)(x+1) + ___ Colmeremo lo spazio vuoto mentre continuiamo a pensare ad altre situazioni. Puoi usare le frazioni invece dei decimali se è più semplice o necessario. 
Se il secondo lancio è una moneta, allora siamo tornati all`inizio. Se anche la seconda volta è una tazza, allora abbiamo finito! 

x = (0.5)(x+1) + (0.25)(x+2) + ___ 
x = (0,5)(x+1) + (0,25)(x+2) + (0,25)(2) Se non sei sicuro di aver riflettuto su ogni possibile situazione, c`è un modo semplice per verificare se l`equazione è completa. Il primo numero in ogni parte dell`equazione rappresenta la probabilità che si verifichi un evento. Questo sarà sempre sommato a 1. Qui 0,5 + 0,25 + 0,25 = 1, quindi sappiamo di aver incluso ogni situazione. 
x = 0,5x + (0,5)(1) + 0,25x + (0,25)(2) + (0,25)(2) x = 0,5x + 0,5 + 0,25x + 0,5 + 0,5 x = 0,75x + 1,5 
x = 0,75x + 1,5 x - 0,75x = 0,75x + 1,5 - 0,75x 0,25x = 1,5 (0,25x)/(0,25) = (1,5)/(0,25) x = 6 In media dovrai lanciare una moneta 6 volte prima di lanciare testa due volte. 

La convinzione di poter essere fortunati o sfortunati lanciando monete (o qualsiasi altro gioco d`azzardo), o che tutta la tua sfortuna ora è finita e la fortuna sarà dalla tua parte, è anche chiamato errore del giocatore (o errore del giocatore). Questo ha a che fare con la tendenza delle persone a prendere decisioni rischiose o stupide quando sentono che la fortuna è dalla loro parte, o che "serie fortunata" o se sentono il loro "la fortuna sta per girare." 
Calcolo del valore atteso
Contenuto
L`aspettativa è un termine statistico e un concetto utilizzato per decidere quanto sarà utile o dannosa un`azione. Per calcolare il valore di aspettativa, è necessario acquisire una buona comprensione di ogni risultato in una particolare situazione e la sua probabilità associata, cioè la probabilità che si verifichi un particolare risultato. I passaggi seguenti forniscono alcuni esercizi di esempio per aiutarti a comprendere il concetto di valore atteso.
Passi
Metodo 1 di 3: Un primo semplice problema

1. Leggi il compito. Prima di iniziare a pensare a tutti i possibili risultati e probabilità, è importante comprendere bene il problema. Ad esempio, un gioco di dadi che costa 10 € a partita. Un dado a 6 facce viene lanciato una volta e le tue vincite dipendono dal numero che ottieni. Se esce un 6, vinci 30€; un 5 ti dà $ 20; qualsiasi altro numero non produce nulla.

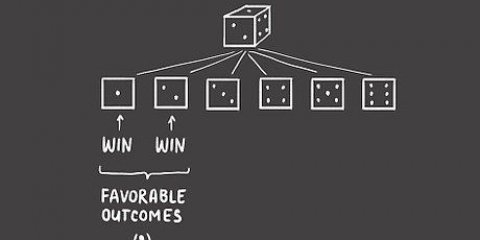
2. Elenca tutti i possibili risultati. Aiuta a elencare tutti i possibili risultati in una determinata situazione. Nell`esempio sopra, ci sono 6 possibili risultati. Questi sono: (1) tira un 1 e perdi 10€, (2) tira un 2 e perdi 10€, (3) tira un 3 e perdi 10€, (4) tira un 4 e perdi 10€ , (5) tira un 5 e vinci 10 €, (6) tira un 6 e vinci 20 €.

3. Determina la probabilità di ogni risultato. In questo caso, la probabilità di 6 risultati qualsiasi è la stessa. La probabilità di ottenere un numero casuale è 1 su 6. Per semplificare la scrittura, scriviamo la frazione (1/6) come decimale usando una calcolatrice: 0,167. Scrivi questa probabilità accanto a ciascun risultato, soprattutto se vuoi risolvere un problema con probabilità diverse per ogni risultato.

4. Registra il valore di ogni risultato. Moltiplica il numero di € di un risultato per la probabilità che quel risultato si realizzi per calcolare quanto denaro quel risultato contribuisce al valore atteso. Ad esempio, il risultato di ottenere un 1 è -$10 e la probabilità di ottenere un 1 è 0,167. Il valore di rotolare un 1 è quindi (-10) * (0,167).

5. Somma il valore di ogni risultato per ottenere il valore atteso di un evento. Per continuare con l`esempio sopra, il valore atteso del gioco dei dadi è: (-10 *0.167) + (-10 *0.167) + (-10 *0.167) + (-10 *0.167) + (10 *0.167) + (20 * 0,167) o - € 1,67. Quindi puoi aspettarti di perdere $ 1,67 ogni volta su questo gioco (a partita).

6. Quali sono le implicazioni del calcolo del valore atteso. Nell`esempio sopra, abbiamo determinato che il guadagno (perdita) previsto sarebbe - $ 1,67 per roll. Questo è un risultato impossibile per 1 partita; puoi perdere 10€, vincere 10€ o vincere 20€. Ma nel lungo periodo, il valore atteso è una probabilità media utile. Se continui a giocare a questo gioco, perderai in media circa $ 1,67 a partita. Un altro modo per pensare al valore atteso è allocare determinati costi (o benefici) al gioco; dovresti giocare a questo gioco solo se pensi che ne valga la pena, come se fosse abbastanza da spendere $ 1,67 ogni volta.
Metodo 2 di 3: calcolo del valore atteso per un risultato specifico

1. Usa questo metodo per calcolare il numero medio di monete che devi lanciare prima che si verifichi un determinato schema. Ad esempio, puoi utilizzare il metodo per scoprire il numero previsto di monete da girare fino a quando non colpisci testa due volte di seguito. Questo problema è un po` più complicato di un problema del valore di aspettativa standard, quindi se non hai familiarità con il valore di aspettativa, leggi prima la parte precedente di questo articolo.

2. Supponiamo di cercare un valore x. Stai cercando di determinare quante monete devi rovesciare in media per ottenere testa due volte di seguito. Facciamo ora un confronto per trovare la risposta. Chiamiamo la risposta che stiamo cercando x. Facciamo il necessario confronto passo dopo passo. Attualmente abbiamo quanto segue:

3. Pensa a cosa succede quando il primo lancio paga.Nella metà dei casi sarà così. Se questo è il caso, allora devi voltarti "sprecato", mentre la probabilità di colpire due teste di fila non è cambiata. Come per il lancio della moneta, ci si aspetta che dovrai lanciare un numero medio di volte per ottenere due teste di fila. In altre parole, dovresti aspettarti di tirare un numero x di volte, più quelle che hai già girato. Sotto forma di equazione:

4. Pensa a cosa succede quando butti la testa. C`è una probabilità di 0,5 (o 1/2) che tirerai una tazza la prima volta. Questo sembra avvicinarsi all`obiettivo di tirare di testa due volte di seguito, ma quanto? Il modo più semplice per scoprirlo è pensare alle tue opzioni nel secondo rotolo:

5. Scopri come calcolare la probabilità che si verifichino entrambi due eventi. Ora sappiamo che hai una probabilità del 50% di ottenere una testa, ma qual è la probabilità di ottenere una testa due volte di seguito?? Per calcolare questa probabilità, moltiplica la probabilità di entrambi insieme. In questo caso è 0,5 x 0,5 = 0,25. Questa è ovviamente anche la probabilità che tu lanci prima testa e poi croce, perché entrambi hanno una probabilità di 0.5 a verificarsi: 0,5 x 0,5 = 0,25.

6. Somma il risultato per "testa, poi croce" al confronto. Ora che abbiamo calcolato la probabilità che questo evento si verifichi, possiamo passare all`espansione dell`equazione. C`è una probabilità di 0,25 (o 1/4) di sprecare due lanci senza fare un ulteriore passo avanti. Ma ora abbiamo ancora bisogno di un numero x di lanci in più in media per ottenere il risultato che vogliamo, più i 2 che abbiamo già tirato. Sotto forma di equazione, questa diventa (0,25)(x+2), che ora possiamo aggiungere all`equazione:

7. Prefissa il risultato "testa di testa" aggiungere al confronto. Se lanci testa con i primi due lanci di monete, hai finito. Hai ottenuto il risultato esattamente in 2 lanci. Come abbiamo stabilito in precedenza, c`è una probabilità di 0,25 che ciò accada, quindi l`equazione per questo è (0,25)(2). La nostra equazione è ora completa:

8. Semplifica l`equazione. Semplifichiamo l`equazione moltiplicando. Ricorda, se vedi qualcosa tra parentesi come questo: (0.5)(x+1), stai moltiplicando 0.5 per ogni termine all`interno della seconda serie di parentesi. Questo ti dà quanto segue: 0,5x + (0.5)(1) o 0,5x + 0,5. Facciamolo per ogni termine nell`equazione, quindi combiniamo quei termini per rendere le cose un po` più semplici:

9. Risolvi per x. Come in ogni equazione dovrai isolare la x su un lato dell`equazione per calcolarla. Ricorda che x ha lo stesso significato di "il numero medio di monete che devi lanciare per ottenere testa due volte di seguito." Quando abbiamo calcolato x, abbiamo anche trovato la nostra risposta.
Metodo 3 di 3: Comprendere il concetto

1. Che cos`è esattamente un valore di aspettativa?. Il valore atteso non è necessariamente il risultato più ovvio o logico. A volte un valore di aspettativa può anche essere un valore impossibile in una determinata situazione. Ad esempio, il valore atteso potrebbe essere +$5 per un gioco con un prezzo non superiore a $10. Ciò che indica il valore di aspettativa è quanto valore ha un particolare evento. Se un gioco ha un valore atteso di +$5, puoi giocarci se ritieni che valga il tempo e il denaro che puoi ottenere per gioco. Se un altro gioco ha un valore atteso di -$20, lo giocherai solo se ritieni che ogni gioco valga i $20.

2. Comprendere il concetto di eventi indipendenti. Nella vita di tutti i giorni, molti di noi pensano di avere un giorno fortunato in cui accadono cose belle e ci aspettiamo che il resto della giornata sia lo stesso. Allo stesso modo possiamo pensare di aver avuto abbastanza incidenti prima di allora e che ora debba succedere qualcosa di veramente bello. Matematicamente, le cose non funzionano in questo modo. Se lanci una moneta normale, c`è esattamente la stessa possibilità che lanci una testa o una moneta. Non importa quante volte hai lanciato; la prossima volta che lanci funziona ancora allo stesso modo. Lanciare la moneta è "indipendente" degli altri calchi, non ne è influenzato.

3. Comprendere la legge dei grandi numeri. Potresti pensare che il valore delle aspettative non sia realmente utile, perché solo raramente ti dice qual è il risultato effettivo di una situazione. Se hai calcolato che il valore atteso di un gioco di roulette è -€1, e giochi 3 volte il gioco, di solito ti ritroverai con -€10, o +€60, o qualche altro risultato. Il "legge dei grandi numeri" aiuta a spiegare perché il valore di aspettativa è più utile di quanto potresti pensare: più spesso giochi, più vicino al valore di aspettativa sarà il risultato medio. Quando si osserva il gran numero di eventi, è probabile che il risultato finale sia vicino al valore atteso.
Consigli
- Per quelle situazioni in cui sono possibili più risultati, puoi creare un foglio di calcolo nel computer per calcolare il valore atteso dai risultati e dalle loro probabilità.
- I calcoli in € di cui sopra funzionano anche in altre valute.
Necessità
- Matita
- Carta
- Calcolatrice
Articoli sull'argomento "Calcolo del valore atteso"
Condividi sui social network:
Popolare