Calcolo della Sequenza di Fibonacci (con Immagini)

Contenuto

Passi
- Metodo 1 di 2: usa una tabella
- Metodo 2 di 2: utilizzo della formula di Binet e della media aurea

La sequenza di Fibonacci è una sequenza di numeri generata sommando i due numeri precedenti nella sequenza. I numeri della serie si vedono spesso in natura e nell`arte, come le spirali e il rapporto aureo. Il modo più semplice per calcolare le serie è preparare una tabella; tuttavia, questo non è pratico se stai cercando il centesimo termine nella sequenza, ad esempio, nel qual caso utilizzerai la formula di Binet.

Passi

Metodo 1 di 2: usa una tabella

Immagine titolata Calculate the Fibonacci Sequence Step 1

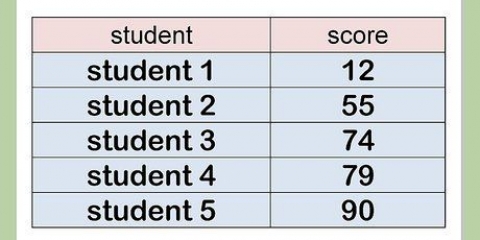
1. Crea una tabella con due colonne. Il numero di righe dipende dal numero di numeri nella sequenza di Fibonacci che vuoi calcolare.

Ad esempio, se vuoi trovare il quinto numero nella sequenza, la tua tabella avrà cinque righe.
Con questo metodo tabellare non è possibile trovare alcun numero più in basso nella sequenza senza prima calcolare tutti i numeri prima di esso. Ad esempio, se vuoi trovare il centesimo numero nella sequenza, dovrai prima trovare i primi 99 numeri. Pertanto il metodo della tabella funziona solo per i numeri all`inizio della sequenza.

Immagine titolata Calculate the Fibonacci Sequence Step 2

2. Immettere la sequenza di numeri nella colonna di sinistra. Ciò significa compilare una sequenza di numeri ordinali consecutivi, a partire da "1°."

Il termine si riferisce alla posizione del numero nella sequenza di Fibonacci.

Ad esempio, se vuoi calcolare il quinto numero della sequenza, scrivi 1°, 2°, 3°, 4°, 5° nella colonna di sinistra. Questo ti aiuterà a identificare i primi cinque termini della sequenza.

Immagine titolata Calculate the Fibonacci Sequence Step 3

3. Metti 1 nella prima riga della colonna di destra. Questo è il punto di partenza della sequenza di Fibonacci. In altre parole, il primo termine della sequenza è 1.

La sequenza di Fibonacci corretta inizia sempre con 1. Se vuoi iniziare con un numero diverso, non troverai lo schema corretto della sequenza di Fibonacci.

Immagine titolata Calculate the Fibonacci Sequence Step 4

4. Conta il primo termine (1) e 0. insieme su. Questo ti darà il secondo numero nella sequenza.

Ricorda che per trovare un dato numero della sequenza di Fibonacci, devi solo sommare i due numeri precedenti.

Per creare la sequenza, 0 viene prima di 1 (il primo termine), quindi: 1 + 0 = 1.

Immagine titolata Calculate the Fibonacci Sequence Step 5

5. Somma il primo termine (1) e il secondo termine (1). Questo ti darà il terzo numero nella sequenza.

1 + 1 = 2. Il terzo termine è 2.

Immagine titolata Calculate the Fibonacci Sequence Step 6

6. Somma il secondo termine (1) e il terzo termine (2) per ottenere il quarto numero della sequenza.

1 + 2 = 3. Il quarto termine è 3.

Immagine titolata Calculate the Fibonacci Sequence Step 7

7. Somma il terzo termine (2) e il quarto termine (3). Ora conosci il quinto numero della sequenza.

2 + 3 = 5. Il quinto termine è 5.

Immagine titolata Calculate the Fibonacci Sequence Step 8

8. Somma i due numeri precedenti per trovare un dato numero nella sequenza di Fibonacci. Se usi questo metodo, usi la formula

F n = F_{n - 1} + F_{n - 2}

$F_{{n}}=F_{{n-1}}+F_{{n-2}}$ . Poiché questa non è una formula chiusa, non puoi usarla per calcolare tutti i termini della serie senza prima calcolare tutti i numeri precedenti.

Metodo 2 di 2: utilizzo della formula di Binet e della media aurea

Immagine titolata Calculate the Fibonacci Sequence Step 9

1. Scrivi la formula:

X n

$x_{{n}}$ =

φ n - (1 - φ)^{n} \sqrt{5}

${frac{phi ^{{n}}-(1-phi )^{{n}}}{{sqrt{5}}}}$ . Nella formula,

X n

$x_{{n}}$ = il termine nella sequenza che stai cercando di trovare,

n

$n$ = il numero di posizione del termine nella serie, e

φ

$phi$ = il rapporto aureo.

Questa è una formula chiusa, quindi puoi calcolare un termine specifico nella serie senza dover calcolare tutti i precedenti.
Questa formula è una formula semplificata derivata dalla formula di Fibonacci di Binet.
La formula applica il rapporto aureo ( $φ$ $phi$ ), perché il rapporto di due numeri consecutivi nella sequenza di Fibonacci è molto simile al rapporto aureo.

Immagine titolata Calculate the Fibonacci Sequence Step 10

2. Regola il numero per n{ displaystyle n} $n$ applicare alla formula. Il

n

$n$ rappresenta il termine che stai cercando nella sequenza.

Ad esempio, se stai cercando il quinto numero della sequenza, inserisci 5. La tua formula ora dovrebbe assomigliare a questa:

X 5

$x_{5}}$ =

φ 5 - (1 - φ)^{5} \sqrt{5}

${frac{phi ^{{5}}-(1-phi )^{{5}}}{{sqrt{5}}}}$ .

Immagine titolata Calculate the Fibonacci Sequence Step 11

3. Sostituisci il rapporto aureo nella formula. Usa 1.618034 come approssimazione del rapporto aureo.

Ad esempio, se cerchi il quinto numero nella sequenza, la formula che hai inserito sarà simile a questa:

X 5

$x_{5}}$ =

(1, 618034) 5 - (1 - 1, 618034)^{5} \sqrt{5}

${frac{(1.618034)^{{5}}-(1-1,618034)^{{5}}}{{sqrt{5}}}}$ .

Immagine titolata Calculate the Fibonacci Sequence Step 12

4. Completa i calcoli tra parentesi. Considera l`ordine delle operazioni aritmetiche calcolando prima la parte tra parentesi:

1 - 1, 618034 = - 0, 618034

$1-1.618034=-0.618034$ .

Nell`esempio, l`equazione diventa

X 5

$x_{5}}$ =

(1, 618034) 5 - (- 0, 618034)^{5} \sqrt{5}

${frac{(1.618034)^{{5}}-(-0.618034)^{{5}}}{{sqrt{5}}}}$ .

Immagine titolata Calculate the Fibonacci Sequence Step 13

5. Calcola gli esponenti. Moltiplica i due numeri tra parentesi al numeratore per l`esponente appropriato.

Nell`esempio,

1, 618034 5 = 11, 090170

$1.618034^{{5}}=11.090170$ ;

- 0, 618034 5 = - 0, 090169

$-0,618034^{{5}}=-0,090169$ . Quindi l`equazione diventa

X 5 = 11, 090170 - (- 0, 090169) \sqrt{5}

$x_{{5}}={frac{11,090170-(-0.090169)}{{sqrt{5}}}}$ .

Immagine titolata Calculate the Fibonacci Sequence Step 14

6. Completa il calcolo. Prima di continuare a dividere, devi prima sottrarre i due numeri nel numeratore.

Nell`esempio,

11, 090170 - (- 0, 090169) = 11, 180339

$11.090170-(-0.090169)=11.180339$ , quindi l`equazione diventa

X 5

$x_{5}}$ =

11, 180339 \sqrt{5}

${frac{11,180339}{{sqrt{5}}}}$ .

Immagine titolata Calculate the Fibonacci Sequence Step 15

7. Dividi per la radice quadrata di cinque. La radice quadrata di cinque è arrotondata a 2,236067.

Nell`incarico di esempio,

11, 180339 2, 236067 = 5, 000002

${frac{11,180339}{2,236067}}=5,000002$ .

Immagine titolata Calculate the Fibonacci Sequence Step 16

8. Arrotonda al numero intero più vicino. La tua risposta è un numero decimale, ma è molto vicino a un numero intero. Questo numero intero rappresenta il numero nella sequenza di Fibonacci.

Se hai utilizzato il rapporto aureo completo e non hai arrotondato nulla, otterrai un numero intero. Tuttavia, è più pratico arrotondare, il che risulterà in un decimale.

Nell`esempio, la tua risposta, calcolata con una calcolatrice, sarà di circa 5.000002. Arrotondato al numero intero più vicino, la tua risposta sarà cinque, che sarà anche il quinto numero nella sequenza di Fibonacci.