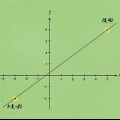
L`asse x è l`asse orizzontale; l`asse y è l`asse verticale. Le coordinate di un punto si scrivono come  .
. Ad esempio, un segmento di linea può avere un punto finale in corrispondenza  e un altro su
e un altro su  .
. 
Ad esempio, con i punti  e
e  , la tua formula sarà simile a questa:
, la tua formula sarà simile a questa: 


Ad esempio:



Ad esempio:



Poiché stai determinando la radice quadrata, potrebbe essere necessario arrotondare la risposta. Poiché stai lavorando da un sistema di coordinate, la tua risposta sarà in generale "unità" e non in centimetri, metri o qualsiasi altra unità. Ad esempio:

 unità.
unità.
Calcolo della lunghezza di una linea utilizzando la formula della distanza
Puoi misurare la lunghezza di una linea verticale o orizzontale in un sistema di coordinate semplicemente aggiungendo le coordinate; tuttavia, misurare la lunghezza di una linea diagonale è un po` più complicato. È possibile utilizzare la formula della distanza per determinare la lunghezza di tale linea. Questa formula è in realtà il teorema di Pitagora, che diventa chiaro quando immagini il segmento di retta come l`ipotenusa di un triangolo rettangolo. Utilizzando una semplice formula geometrica, misurare le linee lungo un certo numero di coordinate diventa un compito relativamente semplice.
Passi
Parte 1 di 2: Scrivere la formula

1. Scrivi la formula della distanza. La formula lo afferma  , per cui
, per cui  è uguale alla distanza della linea,
è uguale alla distanza della linea,  è uguale alle coordinate del primo punto finale del segmento di linea, e
è uguale alle coordinate del primo punto finale del segmento di linea, e  è uguale alle coordinate del secondo punto finale del segmento di linea.
è uguale alle coordinate del secondo punto finale del segmento di linea.
 , per cui
, per cui  è uguale alla distanza della linea,
è uguale alla distanza della linea,  è uguale alle coordinate del primo punto finale del segmento di linea, e
è uguale alle coordinate del primo punto finale del segmento di linea, e  è uguale alle coordinate del secondo punto finale del segmento di linea.
è uguale alle coordinate del secondo punto finale del segmento di linea.
2. Determina le coordinate dei punti finali del segmento di linea. Questi potrebbero essere già stati dati. In caso contrario, contare lungo l`asse x e l`asse y per trovare le coordinate.
 .
. e un altro su
e un altro su  .
.
3. Applicare le coordinate alla formula della distanza. Assicurati di inserire i valori per le variabili corrette. Il due  -le coordinate sono tra le prime parentesi e le due
-le coordinate sono tra le prime parentesi e le due  -le coordinate sono all`interno delle due parentesi successive.
-le coordinate sono all`interno delle due parentesi successive.
 -le coordinate sono tra le prime parentesi e le due
-le coordinate sono tra le prime parentesi e le due  -le coordinate sono all`interno delle due parentesi successive.
-le coordinate sono all`interno delle due parentesi successive. e
e  , la tua formula sarà simile a questa:
, la tua formula sarà simile a questa: 
Parte 2 di 2: Calcolo della distanza

1. Calcola la somma meno tra parentesi. Secondo l`ordine delle operazioni, ogni calcolo tra parentesi deve essere calcolato per primo.
- Ad esempio:

2. Al quadrato il valore tra parentesi. L`ordine delle operazioni prevede che poi si debbano calcolare le potenze.



3. Somma i numeri sotto il segno radicale. Puoi eseguire questo calcolo come se stessi lavorando con numeri interi.



4. Risolvere per D  . Per approssimare la risposta finale, trova la radice quadrata della somma sotto il radicale.
. Per approssimare la risposta finale, trova la radice quadrata della somma sotto il radicale.
 . Per approssimare la risposta finale, trova la radice quadrata della somma sotto il radicale.
. Per approssimare la risposta finale, trova la radice quadrata della somma sotto il radicale.
 unità.
unità.Consigli
- Non confondere questa formula con altre, come la formula del punto medio, la formula della pendenza o l`equazione di una retta.
- Tenere presente l`ordine delle operazioni quando si calcola la risposta. Prima sottrarre, quindi elevare al quadrato la differenza, quindi aggiungere e quindi calcolare la radice quadrata.
Articoli sull'argomento "Calcolo della lunghezza di una linea utilizzando la formula della distanza"
Condividi sui social network:
Simile
Popolare