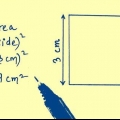
I due lati più corti del triangolo sono i lati del quadrato: ognuno ha una lunghezza S. L`ipotenusa è la diagonale del quadrato, D. 


Semplificare: 
Dividi entrambi i lati per due: 
Zona = 
Zona = 

Ad esempio, supponiamo che un quadrato abbia una diagonale di 10 cm. Zona = 
=
= 50 cm. Ad esempio, un quadrato con una diagonale di 10 cm ha i lati di lunghezza  centimetro.
centimetro. Se vuoi trovare sia la lunghezza di un lato che l`area della diagonale, puoi prima usare questa formula e poi quadrare la risposta per l`area: Area  centimetro. Questo è un po` meno accurato, perché
centimetro. Questo è un po` meno accurato, perché  è un numero irrazionale che potrebbe presentare errori di arrotondamento.
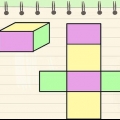
è un numero irrazionale che potrebbe presentare errori di arrotondamento. Disegna un quadrato su carta. Assicurati che tutti i lati siano uguali. Misura la diagonale. Disegna un secondo quadrato con quella lunghezza dei lati del quadrato. Traccia una copia del tuo primo quadrato in modo da averne due. Ritaglia tutti e tre i quadrati. Taglia i due quadrati più piccoli in forme che si adattino al quadrato grande. Devono riempire perfettamente lo spazio, per mostrare che l`area del quadrato grande è esattamente il doppio dell`area del quadrato più piccolo.
Calcolo dell'area di un quadrato usando la diagonale
Contenuto
La formula più comune per l`area di un quadrato è semplice: è la lunghezza di uno dei suoi lati al quadrato, o s. Ma a volte conosci solo la lunghezza della diagonale di un quadrato, la linea tra due vertici opposti. Se hai familiarità con i triangoli rettangoli, puoi ricavare una nuova formula con la diagonale come unica variabile.
Passi
Parte 1 di 2: Calcolo dell`area di un quadrato

1. Disegna il tuo quadrato. Un quadrato ha quattro lati uguali. Diciamo che ogni lato ha una lunghezza di `s`.

2. Usa la formula standard per l`area di un quadrato. L`area di un quadrato è uguale alla sua lunghezza moltiplicata per la sua larghezza. Perché ogni lato S diventa formula Area = s x s = s. Questo si rivelerà presto utile.

3. Collega due angoli opposti per formare una diagonale. La misura di questa diagonale diventa D unità. Questa diagonale divide il quadrato in due triangoli rettangoli.

4.Usa il teorema di Pitagora per uno dei triangoli. Il teorema di Pitagora è una formula per trovare l`ipotenusa (lato più lungo) di un triangolo rettangolo: (lato A) + (lato B) = (ipotenusa) o  . Ora che il quadrato è stato diviso a metà, puoi usare questa formula su uno dei triangoli rettangoli:
. Ora che il quadrato è stato diviso a metà, puoi usare questa formula su uno dei triangoli rettangoli:
 . Ora che il quadrato è stato diviso a metà, puoi usare questa formula su uno dei triangoli rettangoli:
. Ora che il quadrato è stato diviso a metà, puoi usare questa formula su uno dei triangoli rettangoli:

5. Disporre l`equazione in modo che s sia su un lato. Ricordiamo che sappiamo che l`area del quadrato è s. Se riesci a isolare s su un lato, allora hai una nuova equazione per l`area:






6. Usa questa formula con un quadrato di esempio. Questi passaggi hanno dimostrato che la formula Area =  vale per tutti i quadrati. Immettere la lunghezza della diagonale per D e risolvere.
vale per tutti i quadrati. Immettere la lunghezza della diagonale per D e risolvere.
 vale per tutti i quadrati. Immettere la lunghezza della diagonale per D e risolvere.
vale per tutti i quadrati. Immettere la lunghezza della diagonale per D e risolvere.
=

= 50 cm.
Parte 2 di 2: informazioni aggiuntive
1. Trova la diagonale della lunghezza di un lato. Il teorema di Pitagora per un quadrato di lato S e diagonale D darti la formula  in poi. Risolvi per `d` se conosci le lunghezze dei lati e vuoi determinare la lunghezza della diagonale:
in poi. Risolvi per `d` se conosci le lunghezze dei lati e vuoi determinare la lunghezza della diagonale:
 in poi. Risolvi per `d` se conosci le lunghezze dei lati e vuoi determinare la lunghezza della diagonale:
in poi. Risolvi per `d` se conosci le lunghezze dei lati e vuoi determinare la lunghezza della diagonale: - Ad esempio, se un quadrato ha i lati di 7 cm, la diagonale è d = 7√2 cm, ovvero circa 9,9 cm.
- Se non hai una calcolatrice, puoi usare 1.4 come stima di √2.
2. Determina la lunghezza di un lato usando la diagonale. È data la diagonale e sai che è la diagonale di un quadrato  quindi puoi dividere entrambi i lati per
quindi puoi dividere entrambi i lati per  a
a  ottenere.
ottenere.
 quindi puoi dividere entrambi i lati per
quindi puoi dividere entrambi i lati per  a
a  ottenere.
ottenere. centimetro.
centimetro. centimetro. Questo è un po` meno accurato, perché
centimetro. Questo è un po` meno accurato, perché  è un numero irrazionale che potrebbe presentare errori di arrotondamento.
è un numero irrazionale che potrebbe presentare errori di arrotondamento.3. Interpreta la formula della superficie. La formula Area =  sembra essere matematicamente corretto, ma c`è un modo per verificarlo direttamente? Bene,
sembra essere matematicamente corretto, ma c`è un modo per verificarlo direttamente? Bene,  è l`area di un secondo quadrato con la diagonale come lato. Perché la formula completa
è l`area di un secondo quadrato con la diagonale come lato. Perché la formula completa  puoi ragionare sul fatto che questo secondo quadrato ha esattamente il doppio dell`area del quadrato originale. Puoi testarlo tu stesso:
puoi ragionare sul fatto che questo secondo quadrato ha esattamente il doppio dell`area del quadrato originale. Puoi testarlo tu stesso:
 sembra essere matematicamente corretto, ma c`è un modo per verificarlo direttamente? Bene,
sembra essere matematicamente corretto, ma c`è un modo per verificarlo direttamente? Bene,  è l`area di un secondo quadrato con la diagonale come lato. Perché la formula completa
è l`area di un secondo quadrato con la diagonale come lato. Perché la formula completa  puoi ragionare sul fatto che questo secondo quadrato ha esattamente il doppio dell`area del quadrato originale. Puoi testarlo tu stesso:
puoi ragionare sul fatto che questo secondo quadrato ha esattamente il doppio dell`area del quadrato originale. Puoi testarlo tu stesso:Consigli
- Questa semplice equazione è utilizzata in molti campi, tra cui cristallografia, chimica e arte. Ad esempio, puoi usarlo per calcolare l`area di un paesaggio che vedi durante il rilievo, o quando usi la prospettiva in fotografia o pittura, misurando la distanza percorsa e immaginando una griglia di quella distanza come diagonale.
- Se vuoi adottare un approccio più visivo alla matematica, o imparare a usare grafici e diagrammi nell`arte, o esplorare il percorso a spirale di una particella, dai un`occhiata ad alcuni articoli su Microsoft Excel, matematica, fogli di calcolo e grafica.
- Se non hai una calcolatrice ma hai bisogno di una stima più accurata della radice quadrata di due, ci sono modi per farlo per farlo a mano. Un esempio di questo è il metodo di Newton-Raphson.
Articoli sull'argomento "Calcolo dell'area di un quadrato usando la diagonale"
Condividi sui social network:
Simile
Popolare