Calcolo dell'altezza di un prisma

Contenuto

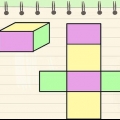
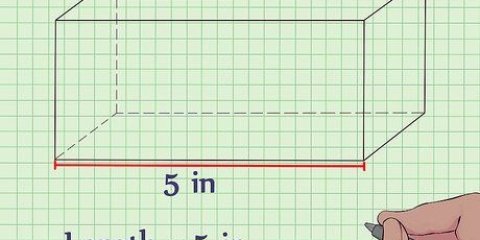
Un prisma è una figura tridimensionale con due basi parallele, che sono congruenti.La forma della base determina di che tipo di prisma si tratta, ad esempio un prisma rettangolare o triangolare. Trattandosi di una forma 3D, non è raro voler calcolare il volume di un prisma; tuttavia, per questo è necessaria l`altezza del prisma. Trovare l`altezza è possibile quando hai ricevuto informazioni sufficienti: il volume, l`area e il perimetro della base. Le formule descritte nei metodi seguenti sono adatte per prismi con basi di qualsiasi forma, a condizione che tu conosca la formula per trovare l`area di quella forma.

Passi

Metodo 1 di 4: Trovare l`altezza di un prisma rettangolare di volume noto

Immagine titolata Trova l`altezza di un prisma Step 1
1. Usa la formula per il volume di un prisma. Il volume di un prisma può essere trovato usando la formula V=unh{ displaystyle V = Ah}V=Ah, per cui V{ displaystyle V}V è uguale al volume del prisma, un{ displaystyle A}un è uguale all`area di una base, e h{ displaystyle h}h è uguale all`altezza del prisma.
  • La base di un prisma è uno dei suoi lati congruenti. Poiché tutti i lati opposti di un prisma rettangolare sono congruenti, qualsiasi lato può essere utilizzato come piano terra, purché tu sia coerente con i tuoi calcoli.
Immagine titolata Trova l`altezza di un prisma Step 2
2. Applicare il volume alla formula. Se non conosci il volume, non puoi utilizzare questo metodo.
  • Ad esempio, se il volume del prisma è 64 m3{displaystyle m^{3}}m^{{3}}), la tua formula sarà simile a questa:
    64=unh{displaystyle 64=Ah}64=Ah
    • Immagine titolata Trova l`altezza di un prisma Step 3
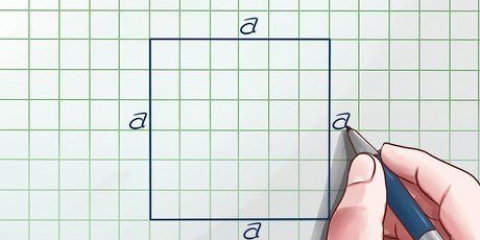
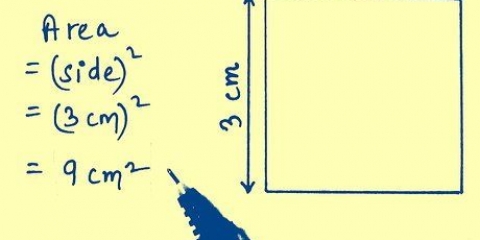
    3. Trova l`area della base. Per trovare l`area, devi conoscere la lunghezza e la larghezza della base (o di un lato, se la base è un quadrato). Usa la formula un=lw{ displaystyle A = lw}A=lw per determinare l`area di un rettangolo.
  • Ad esempio, se la base è un rettangolo lungo 8 metri e largo 2 metri, si calcola l`area come segue:
    un=(8)(2){displaystyle A=(8)(2)}A=(8)(2)
    un=16m2{displaystyle A=16m^{2}}A=16 milioni^{{2}}
    • Immagine titolata Trova l`altezza di un prisma Step 4
    4. Sostituisci l`area della base nel volume della formula del prisma. Assicurati di sostituire la variabile un{ displaystyle A}un.
  • Ad esempio, se hai calcolato che l`area della base è 16 m, la tua formula sarà simile a questa:
    64=16h{displaystyle 64=16h}64=16h
    • Immagine titolata Trova l`altezza di un prisma Step 5
    5. Risolvi l`equazione per h{ displaystyle h}h. Ora conosci l`altezza del tuo prisma.
  • Ad esempio, nell`equazione 64=16h{displaystyle 64=16h}64=16h, devi dividere ogni lato per 16 om h{ displaystyle h}h calcolare. Così:
    6416=16h16{displaystyle {frac {64}{16}}={frac {16h}{16}}}{frac{64}{16}}={frac{16h}{16}}
    4=h{ displaystyle 4 = h}4=h
    Quindi l`altezza del prisma rettangolare è di 4 metri.

    • Metodo 2 di 4: Determinazione dell`altezza di un prisma triangolare di volume noto

    Immagine titolata Trova l`altezza di un prisma Step 6
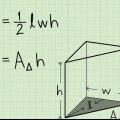
    1. Scrivi la formula per il volume di un prisma. Il volume di qualsiasi prisma può essere trovato usando la formula V=unh{ displaystyle V = Ah}V=Ah,per cui V{ displaystyle V}V è uguale al volume del prisma, un{ displaystyle A}un è uguale all`area di una base, e h{ displaystyle h}h è uguale all`altezza del prisma.
    • La base di un prisma è uno dei suoi lati congruenti. La base di un prisma triangolare è un triangolo. I lati sono rettangoli.
    Immagine titolata Trova l`altezza di un prisma Step 7
    2. Applicare il volume alla formula. Se non conosci il volume, non puoi utilizzare questo metodo.
  • Ad esempio, se sai che il volume del prisma è di 840 metri cubi (m3{displaystyle m^{3}}m^{{3}}), la tua formula sarà simile a questa:
    840=unh{displaystyle 840=Ah}840=Ah
    • Immagine titolata Trova l`altezza di un prisma Step 8
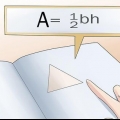
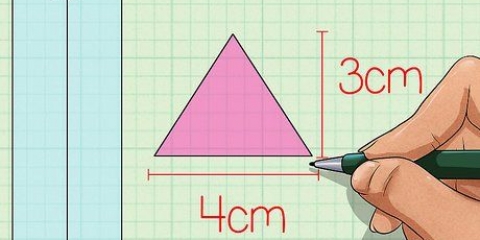
    3. Trova l`area della base. Per trovare l`area, devi conoscere la lunghezza della base del triangolo e l`altezza del triangolo. Usa la formula un=12(B)(h){displaystyle A={frac {1}{2}}(b)(h)}A={frac{1}{2}}(b)(h) per determinare l`area di un triangolo.
  • Se conosci la lunghezza di tutti e tre i lati di un triangolo, puoi calcolare l`area usando la formula di Heron.leggere Calcola l`area di un triangolo per istruzioni dettagliate.
  • Ad esempio, se la base del triangolo è 12 metri e l`altezza del triangolo è 7 metri, trova l`area come segue:
    un=12(12)(7){displaystyle A={frac {1}{2}}(12)(7)}A={frac{1}{2}}(12)(7)
    un=12(84){displaystyle A={frac {1}{2}}(84)}A={frac{1}{2}}(84)
    un=42{displaystyle A=42}A=42
    • Immagine titolata Trova l`altezza di un prisma Step 9
    4. Sostituisci l`area della base nel volume della formula del prisma. Assicurati di sostituire la variabile un{ displaystyle A}un.
  • Ad esempio, se sai che l`area della base è 42 m2, la tua formula sarà simile a questa:
    840=42h{displaystyle 840=42h}840=42 ore
    • Immagine titolata Trova l`altezza di un prisma Step 10
    5. Risolvi l`equazione per h{ displaystyle h}h. Ora conosci l`altezza del tuo prisma.
  • Ad esempio, nell`equazione 840=42h{displaystyle 840=42h}840=42 ore, devi dividere ogni lato per 42 per determinare h{ displaystyle h}h. Così:
    84042=42h42{displaystyle {frac {840}{42}}={frac {42h}{42}}}{frac{840}{42}}={frac{42h}{42}}
    20=h{ displaystyle 20 = h}20=h
  • Quindi, l`altezza del tuo prisma triangolare è di 20 metri.

    • Metodo 3 di 4: Trovare l`altezza di un prisma rettangolare usando la sua area

    Immagine titolata Trova l`altezza di un prisma Step 11
    1. Scrivi la formula per l`area di un prisma. La formula per l`area di un prisma è Sun=2B+Ph{ displaystyle SA = 2B + Ph}SA=2B+F, per cui Sun{ displaystyle SA}SA è uguale alla superficie, B{ displaystyle B}B è uguale all`area della base, P{ displaystyle P}P è uguale al perimetro della base, e h{ displaystyle h}h è uguale all`altezza del prisma.
    • Affinché questo metodo funzioni, è necessario conoscere l`area del prisma, nonché la lunghezza e la larghezza della base.
    Immagine titolata Trova l`altezza di un prisma Step 12
    2. Sostituisci l`area del prisma nella formula. Se la superficie è sconosciuta, questo metodo non funzionerà.
  • Ad esempio, se l`area è 1460 cm, la tua formula sarebbe simile a questa:
    1460=2B+Ph{ displaystyle 1460 = 2B+F}1460=2B+F
    • Immagine titolata Trova l`altezza di un prisma Step 13
    3. Trova l`area della base. Per trovare l`area, devi conoscere la lunghezza e la larghezza della base (o un lato, se la base è un quadrato). Usa la formula un=lw{ displaystyle A = lw}A=lw per determinare l`area di un rettangolo.
  • Ad esempio, se la base è un rettangolo con una lunghezza di 8 cm e una larghezza di 2 cm, trovare l`area come segue:
    un=(8)(2){displaystyle A=(8)(2)}A=(8)(2)
    un=16{displaystyle A=16}A=16
    • Immagine titolata Trova l`altezza di un prisma Step 14
    4. Sostituisci l`area della base nella formula per l`area di un prisma e semplifica. Assicurati di compilare la lettera B{ displaystyle B}B.
  • Ad esempio, se l`area della base è 16, la tua formula sarebbe simile a questa:
    1460=2(16)+Ph{displaystyle 1460=2(16)+Ph}1460=2(16)+F
    1460=32+Ph{displaystyle 1460=32+Fh}1460=32+F
    • Immagine titolata Trova l`altezza di un prisma Step 15
    5. Determina il perimetro della base. Per trovare il perimetro di un rettangolo, somma le lunghezze di tutti e quattro i lati o moltiplica la lunghezza di un lato per 4 se è un quadrato.
  • Ricorda che i lati opposti di un rettangolo hanno la stessa lunghezza.
  • Ad esempio, se la base è un rettangolo con una lunghezza di 8 cm e una larghezza di 2 cm, trova il perimetro come segue:
    P=8+2+8+2{displaystyle P=8+2+8+2}P=8+2+8+2
    P=20{displaystyle P=20}P=20
    • Immagine titolata Trova l`altezza di un prisma Step 16
    6. Sostituisci il perimetro della base nella formula per l`area di un prisma. Assicurati di sostituire la lettera P{ displaystyle P}P.
  • Ad esempio, se il perimetro della base è 20, la tua formula sarebbe simile a questa:
    1460=32+20h{displaystyle 1460=32+20h}1460=32+20 ore
    • Immagine titolata Trova l`altezza di un prisma Step 17
    7. Risolvi l`equazione per h{ displaystyle h}h. Ora conosci l`altezza del tuo prisma.
  • Ad esempio, nell`equazione 1460=32+20h{displaystyle 1460=32+20h}1460=32+20 ore prima sottrarre 32 da ciascun lato, quindi dividere ciascun lato per 20. Così:
    1460=32+20h{displaystyle 1460=32+20h}1460=32+20 ore
    1428=20h{displaystyle 1428=20h}1428=20 ore
    142820=20h20{displaystyle {frac {1428}{20}}={frac {20h}{20}}}{frac{1428}{20}}={frac{20h}{20}}
    71.4=h{ displaystyle 71.4=h}71,4=h
  • Quindi l`altezza del tuo prisma è 71,4 cm.

    • Metodo 4 di 4: Determina l`altezza di un prisma triangolare usando la sua area

    Immagine titolata Trova l`altezza di un prisma Step 18
    1. Scrivi la formula per l`area di un prisma. La formula per l`area di un prisma è Sun=2B+Ph{ displaystyle SA = 2B + Ph}SA=2B+F, per cui Sun{ displaystyle SA}SA è uguale alla superficie, B{ displaystyle B}B è uguale all`area della base, P{ displaystyle P}P è uguale al perimetro della base, e h{ displaystyle h}h è uguale all`altezza del prisma.
    • Affinché questo metodo funzioni, è necessario conoscere l`area del prisma, nonché l`area della base triangolare e la lunghezza di tutti e tre i lati della base.
    Immagine titolata Trova l`altezza di un prisma Step 19
    2. Sostituisci l`area del prisma nella formula. Se la superficie non è nota, questo metodo non funzionerà.
  • Ad esempio, se l`area è 1460 cm, la tua formula sarebbe simile a questa:
    1460=2B+Ph{ displaystyle 1460 = 2B+F}1460=2B+F
    • Immagine titolata Trova l`altezza di un prisma Step 20
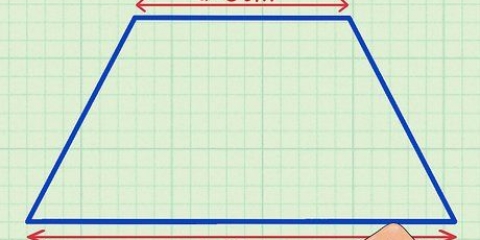
    3. Trova l`area della base. Per trovare l`area, devi conoscere la lunghezza della base del triangolo e l`altezza del triangolo. Usa la formula un=12(B)(h){displaystyle A={frac {1}{2}}(b)(h)}A={frac{1}{2}}(b)(h) per determinare l`area di un triangolo.
  • Se conosci la lunghezza di tutti e tre i lati di un triangolo, puoi determinare l`area usando la formula di Heron.leggere Calcola l`area di un triangolo per le istruzioni complete.
  • Ad esempio, se la base del triangolo è 8 cm e l`altezza del triangolo è 4 cm, si calcola l`area come segue:
    un=12(8)(4){displaystyle A={frac {1}{2}}(8)(4)}A={frac{1}{2}}(8)(4)
    un=12(32){displaystyle A={frac {1}{2}}(32)}A={frac{1}{2}}(32)
    un=16{displaystyle A=16}A=16
    • Immagine titolata Trova l`altezza di un prisma Step 21
    4. Sostituisci l`area della base nella formula per l`area di un prisma e semplifica. Sostituto per B{ displaystyle B}B.
  • Ad esempio, se l`area della base è 16, la tua formula sarebbe simile a questa:
    1460=2(16)+Ph{displaystyle 1460=2(16)+Ph}1460=2(16)+F
    1460=32+Ph{displaystyle 1460=32+Fh}1460=32+F
    • Immagine titolata Trova l`altezza di un prisma Step 22
    5. Determina il perimetro della base. Per trovare il perimetro di un triangolo, somma le lunghezze di tutti e tre i lati.
  • Ad esempio, se la base è un triangolo di lunghezza 8, 4 e 9 cm, si calcola il perimetro come segue:
    P=8+4+9{displaystyle P=8+4+9}P=8+4+9
    P=21{ displaystyle P = 21}P=21
    • Immagine titolata Trova l`altezza di un prisma Step 23
    6. Sostituisci il perimetro della base nella formula per l`area di un prisma. Assicurati di sostituire P{ displaystyle P}P.
  • Ad esempio, supponiamo che il perimetro della base sia 21, la tua formula sarà simile a questa:
    1460=32+21h{displaystyle 1460=32+21h}1460=32+21 ore
    • Immagine titolata Trova l`altezza di un prisma Step 24
    7. Risolvi l`equazione per h{ displaystyle h}h. Ora conosci l`altezza del tuo prisma.
  • Ad esempio, nell`equazione 1460=32+21h{displaystyle 1460=32+21h}1460=32+21 ore, devi prima sottrarre 32 da ciascun lato, quindi dividere ogni lato per 21. Così:
    1460=32+21h{displaystyle 1460=32+21h}1460=32+21 ore
    1428=21h{displaystyle 1428=21h}1428=21h
    142821=21h21{displaystyle {frac {1428}{21}}={frac {21h}{21}}}{frac{1428}{21}}={frac{21h}{21}}
    68=h{ displaystyle 68 = h}68=h
  • Quindi, l`altezza del tuo prisma è di 68 cm.

    • Necessità

    • Penna/matita e carta o calcolatrice (opzionale)

    It.FaqCartx.info / Educazione e comunicazione
    Condividi sui social network:
    Nuovo
    Trattamento della fascite plantare
    Trattamento della fascite plantare
    Stampa le ricevute di uber
    Stampa le ricevute di uber
    Aglio essiccato
    Aglio essiccato
    Salvare un cespuglio di rose morente
    Salvare un cespuglio di rose morente
    Pastinaca arrosto
    Pastinaca arrosto
    Installa i controller di gioco usb in windows 8
    Installa i controller di gioco usb in windows 8