Es: se l`altezza della base triangolare è 5 cm e la base del prisma triangolare è 4 cm, allora l`area della base è 1/2 x 5 cm x 4 cm, pari a 10 cm. 

Es: 10 cm x 7 cm = 70 cm 


Es: Lunghezza = 3 cm. 
Es: 3 cm = 3 cm. * 3 cm. * 3 cm. = 27 cm. 


Es: Lunghezza = 10 cm. 
Es: Larghezza = 8 cm. 
Es: Altezza = 5 cm. 
Es: 10 cm. * 8 cm. * 5 cm = 400 cm. 


Supponiamo che base 1 = 8 cm, base 2 = 6 cm e altezza = 10 cm. Es: 1/2 x (6 + 8) x 10 = 1/2 x 14 cm x 10 cm = 80 cm. 

80 cm x 12 cm = 960 cm. 


A = 1/2 x 5 x lato x apotema A = 1/2 x 5 x 6 cm x 7 cm = 105 cm 

105 cm x 10 cm = 1050 cm 
Calcolo del volume di un prisma
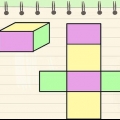
Un prisma è una figura geometrica con due estremità identiche e lati piatti. Il prisma prende il nome dalla forma della sua base, quindi un prisma a base triangolare è chiamato a "Prisma triangolare." Per calcolare il volume di un prisma, devi solo calcolare l`area della base e moltiplicarla per l`altezza: calcolare l`area della base può essere la parte difficile. Ecco come calcolare il volume di vari prismi.
Passi
Metodo 1 di 5: Calcolo del volume di un prisma triangolare

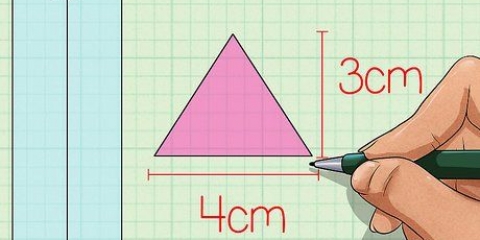
1. Scrivi la formula per trovare il volume di un prisma triangolare. La formula è V = 1/2 x lunghezza x larghezza x altezza. Ma scomponiamo ulteriormente questa formula, per ottenere la formula V = area o base x altezza usare. Puoi calcolare l`area della base, usando la formula per trovare l`area di un triangolo: moltiplica 1/2 per la lunghezza e la larghezza della base.

2. Determina l`area del piano di base. Per trovare il volume di un prisma triangolare, devi prima determinare l`area della base triangolare. Trova l`area della base del prisma moltiplicando 1/2 per la base del triangolo per l`altezza.

3. Determina l`altezza. Supponiamo che l`altezza di questo prisma triangolare sia 7 cm.

4. Moltiplica l`area della base triangolare per l`altezza. Moltiplica l`area della base per l`altezza. Moltiplica la base per l`altezza e ottieni il volume del prisma triangolare.

5. Dai la tua risposta in unità cubiche. Dovresti sempre usare le unità cubiche quando calcoli un volume perché stai lavorando con oggetti tridimensionali. La risposta finale è 70 cm.
Metodo 2 di 5: Calcolo del volume di un cubo

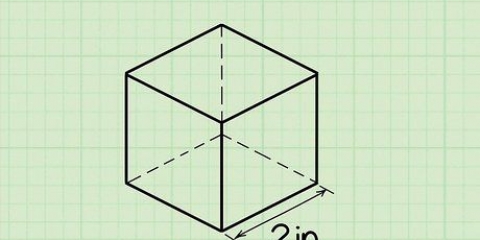
1. Scrivi la formula per trovare il volume di un cubo. La formula è V = lato. Un cubo è un prisma con 3 lati uguali.

2. Determina la lunghezza di 1 lato del cubo. Tutti i lati sono uguali, quindi non importa quale scegli.

3. Il potere del tre. Moltiplica il numero per se stesso due volte per ottenere il numero cubico. Un esempio è "ax ax a". Poiché tutte le lunghezze dei lati sono uguali, moltiplicare due lati per l`area della base e un terzo lato per l`altezza. Puoi pensare a questo come a una moltiplicazione della lunghezza, larghezza e altezza, che sono tutte uguali.

4. Dai la tua risposta in unità cubiche.. La risposta finale è 27 cm.
Metodo 3 di 5: Calcolo del volume di un prisma rettangolare

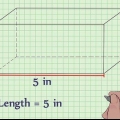
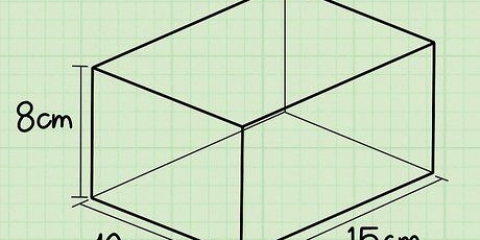
1. Scrivi la formula per trovare il volume di un prisma rettangolare. La formula è V = lunghezza * larghezza * altezza. Un prisma rettangolare è un prisma a base rettangolare.

2. Determina la lunghezza. La lunghezza è il lato più lungo della superficie piana del rettangolo, sopra o sotto il prisma rettangolare.

3. Determina la larghezza. La larghezza del prisma rettangolare è il lato più corto della superficie piana di un rettangolo, nella parte superiore o inferiore della forma.

4. Determina l`altezza. L`altezza è quella parte del prisma rettangolare che è verticale. Puoi immaginare l`altezza del prisma rettangolare come quella parte che si estende da un rettangolo e ne fa una figura tridimensionale.

5. Moltiplica la lunghezza, la larghezza e l`altezza. Moltiplicare questi in qualsiasi ordine per il prodotto. Usa questo metodo per trovare l`area della base rettangolare (10 x 8) e poi il volume moltiplicandolo per l`altezza, 5. Tuttavia, per trovare il volume di questo prisma, puoi moltiplicare le lunghezze degli sono in qualsiasi ordine.

6. Dai la tua risposta in unità cubiche. La risposta finale è 400 cm.
Metodo 4 di 5: Calcolo del volume di un prisma trapezoidale

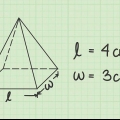
1. Scrivi la formula per calcolare il volume di un trapezio. La formula è: V = [1/2 x (base1 + base2) x altezza] x altezza del prisma. Usa la prima parte per l`area della base del prisma prima di continuare.

2. Trova l`area della base. Per fare ciò, inserisci l`area della parte superiore e inferiore nella formula, insieme all`altezza.

3. Determina l`altezza del prisma. Supponiamo che l`altezza del prisma sia 12 cm.

4. Moltiplica l`area della base per l`altezza. Per calcolare il volume del trapezio, moltiplica l`area della base per l`altezza.

5. Dai la tua risposta in unità cubiche. La risposta finale è 960 cm
Metodo 5 di 5: Calcola il volume di un prisma pentagonale regolare

1. Scrivi la formula per trovare il volume di un prisma pentagonale regolare. La formula è V = [1/2 x 5 x lato x apotema] x altezza del prisma. Puoi usare la prima parte della formula per trovare l`area della base pentagonale. Pensa a questo come alla determinazione dell`area dei 5 triangoli che insieme formano un poligono regolare. Il lato è la larghezza di 1 triangolo e l`apotema è l`altezza di uno dei triangoli.Ora moltiplichi per 1/2 perché fa parte della ricerca dell`area di un triangolo e poi lo moltiplichi per 5 perché ci sono 5 triangoli in un pentagono.
- Per ulteriori informazioni sulla determinazione dell`apotema, vedere qui.

2. Trova l`area della base pentagonale. Supponiamo che la lunghezza di un lato sia 6 cm e la lunghezza dell`apotema sia 7 cm. Inserisci i numeri nella formula:

3. Determina l`altezza. Impostare l`altezza dello stampo è di 10 cm.

4. Moltiplica l`area della base pentagonale per l`altezza. Moltiplica l`area della base pentagonale, 105 cm, per l`altezza, 10 cm, per trovare il volume del comune prisma pentagonale.

5. Dai la tua risposta in unità cubiche. La risposta finale è 1050 cm.
Consigli
- Provare "base" da non confondere con "piano di base".Un piano di base si riferisce alla forma bidimensionale che è la base del prisma (di solito la parte superiore e inferiore).Ma quel piano di base può avere la sua base --- uno dei lati della forma del piano, usato per trovare l`area di quella forma.
Articoli sull'argomento "Calcolo del volume di un prisma"
Condividi sui social network:
Simile
Popolare