Come Calcolare il Volume di una Piramide Quadrata

Contenuto

Passi
Consigli

Una piramide quadrata è una figura tridimensionale con una base quadrata e inclinazioni triangolari che si incontrano in un punto sopra la base. Nel caso in cui $S$ $S$ è la lunghezza di uno dei lati del quadrato e $h$ $h$ l`altezza della piramide (la distanza perpendicolare dalla base a quel punto), quindi il volume di una piramide quadrata può essere calcolato usando la formula $V = \frac{1}{3} S^{2} h$ $V={frac{1}{3}}s^{2}h$ . Non importa se la piramide ha le dimensioni di un fermacarte o più grande della Piramide di Giza: questa formula funziona per qualsiasi piramide quadrata. Il volume può anche essere calcolato utilizzando l`apotema della piramide.

Passi

Metodo 1 di 3: Determina il volume con l`area della base e l`altezza

Immagine titolata Calculate the Volume of a Square Pyramid Step 01

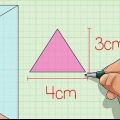
1. Misura la lunghezza del lato della base. Poiché le piramidi quadrate per definizione hanno una base quadrata, tutti i lati della base dovrebbero avere la stessa lunghezza. Quindi con una piramide quadrata devi solo conoscere la lunghezza di uno dei lati.

Supponiamo di avere una piramide a base quadrata i cui lati hanno una lunghezza di $S = 5 centimetro$ $s=5{testo{cm}}$ . Utilizzerai questo valore per calcolare l`area della base.
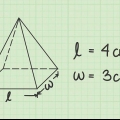
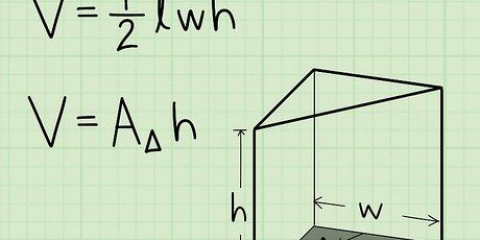
Se i lati della base non sono uguali in lunghezza, allora hai a piramide rettangolare invece di una piramide quadrata. La formula per il volume di una piramide rettangolare è molto simile alla formula per le piramidi quadrate. Nel caso in cui $l$ $l$ è la lunghezza della base della piramide rettangolare e $w$ $w$ la larghezza, quindi il volume della piramide $V = \frac{1}{3} h * l * w$ $V={frac{1}{3}}h*l*w$ .

Immagine titolata Calculate the Volume of a Square Pyramid Step 02

2. Calcola l`area della base. Per determinare il volume, è necessaria prima l`area della base. Lo fai moltiplicando la lunghezza e la larghezza della base. Poiché la base di una piramide quadrata è un quadrato, tutti i lati hanno la stessa lunghezza e l`area della base è uguale al quadrato della lunghezza di uno dei suoi lati (quindi moltiplicato per se stesso).

Nell`esempio i lati della base della piramide sono tutti 5 cm, e si calcola l`area della base come segue:

Superficie = S^{2} = (5 centimetro)^{2} = 25 {centimetro}^{2}

${text{Area}}=s^{2}=(5{text{cm}})^{2}=25{text{cm}}^{2}$

Ricorda che le aree bidimensionali sono espresse in quadrati: centimetri quadrati, metri, chilometri, ecc.

Immagine titolata Calculate the Volume of a Square Pyramid Step 03

3. Moltiplica l`area della base per l`altezza della piramide. Quindi moltiplichi l`area di base per l`altezza della piramide. Come promemoria, l`altezza è la distanza è la lunghezza del segmento di linea dalla sommità della piramide alla base, ad angolo retto.

Nell`esempio assumiamo che la piramide abbia un`altezza di 9 cm. In questo caso, moltiplica l`area della base per questo valore, come segue:

25 centimetro 2 * 9 centimetro = 225 {centimetro}^{3}

$25{testo{cm}}^{2}*9{testo{cm}}=225{testo{cm}}^{3}$

Ricorda che i volumi sono espressi in unità cubiche. In questo caso, poiché tutte le misure lineari sono centimetri, il volume è indicato in centimetri cubi.

Immagine titolata Calculate the Volume of a Square Pyramid Step 04

4. Dividi questa risposta per 3. Infine, determini il volume della piramide dividendo il valore che hai appena trovato (moltiplicando l`area della base per l`altezza) per 3. Questo calcola il volume della piramide quadrata.

Nell`esempio, dividi 225 cm per 3 e la risposta è 75 cm per il volume.

Metodo 2 di 3: Determina il volume con l`apotema

Immagine titolata Calculate the Volume of a Square Pyramid Step 05

1. Misura l`apotema della piramide. A volte non viene data l`altezza perpendicolare della piramide (o bisogna misurarla), ma l`apotema. Con l`apotema puoi usare il teorema di Pitagora utilizzare per calcolare l`altezza perpendicolare.

L`apotema di una piramide è la distanza dall`apice al centro di uno dei lati della sua base. Misura al centro di uno dei lati e non a uno degli angoli della base. Per questo esempio assumiamo che l`apotema sia 13 cm e la lunghezza di un lato della base sia 10 cm.
Ricorda che il teorema di Pitagora può essere espresso come equazione $un 2 + B^{2} = C^{2}$ $a^{2}+b^{2}=c^{2}$ , per cui $un$ $un$ e $B$ $B$ le gambe perpendicolari sono del triangolo rettangolo e $C$ $C$ l`ipotenusa.

Immagine titolata Calculate the Volume of a Square Pyramid Step 06

2. Immagina un triangolo rettangolo. Per usare il teorema di Pitagora è necessario un triangolo rettangolo. Immagina un triangolo che divide la piramide a metà e perpendicolare alla base della piramide. L`apotema della piramide, chiamato

l

$l$ , è l`ipotenusa di questo triangolo rettangolo. La base di questo triangolo rettangolo è la metà della lunghezza di

S

$S$ , lato della base quadrata della piramide.

Immagine titolata Calculate the Volume of a Square Pyramid Step 07

3. Assegna variabili ai valori. Il teorema di Pitagora usa le variabili a, b e c, ma è utile sostituirle con variabili significative per il tuo problema. l`apotema

l

$l$ prende il posto di

C

$C$ nel teorema di Pitagora. La gamba del triangolo rettangolo (

\frac{S}{2}

${frac{s}{2}}$ ), prende il posto di

B .

$B$ Vai all`altezza

h

$h$ determinare la piramide, che occupa il posto di

un

$un$ nel teorema di Pitagora.

Questa sostituzione si presenta così:

un 2 + B^{2} = C^{2}

$a^{2}+b^{2}=c^{2}$

h 2 + (\frac{S}{2})^{2} = l^{2}

$h^{2}+({frac{s}{2}})^{2}=l^{2}$

Immagine titolata Calculate the Volume of a Square Pyramid Step 08

4. Usa il teorema di Pitagora per calcolare l`altezza perpendicolare. Utilizzare i valori misurati

S = 10

$s=10$ e

l = 13

$l=13$ . Quindi risolvi l`equazione:

h 2 = l^{2} - (\frac{S}{2})^{2}

$h^{2}=l^{2}-({frac{s}{2}})^{2}$ .....(equazione originale)

h = \sqrt{l} 2 - (\frac{S}{2})^{2}

$h={sqrt{l^{2}-({frac{s}{2}})^{2}}}$ .....(quadrare entrambi i lati)

h = \sqrt{13} 2 - (\frac{10}{2})^{2}

$h={sqrt{13^{2}-({frac{10}{2}})^{2}}}$ .....(inserire valori)

h = \sqrt{169 - 5} 2

$h={sqrt{169-5^{2}}}$ .....(semplificare la frazione)

h = \sqrt{169 - 25}

$h={sqrt{169-25}}$ .....(semplificare quadrato)

h = \sqrt{144}

$h={sqrt{144}}$ .....(sottrarre)

h = 12

$h=12$ .....(semplificare la radice)

Immagine titolata Calculate the Volume of a Square Pyramid Step 09

5. Usa altezza e base per calcolare il volume. Dopo aver applicato questi calcoli al Teorema di Pitagora ora hai le informazioni che ti servono per calcolare il volume della piramide. Usa la formula

V = \frac{1}{3} S^{2} h

$V={frac{1}{3}}s^{2}h$ e risolvili, assicurandoti di dare la risposta in unità quadrate.

Dai calcoli deduciamo che l`altezza della piramide è di 12 cm. Usalo insieme al lato di 10 cm della base per calcolare il volume della piramide:

V = \frac{1}{3} S^{2} h

$V={frac{1}{3}}s^{2}h$

V = \frac{1}{3} (10^{2}) 12

$V={frac{1}{3}}(10^{2})12$

V = \frac{1}{3} (100) (12)

$V={frac{1}{3}}(100)(12)$

V = 400 centimetro 3

$V=400{testo{cm}}^{3}$

Metodo 3 di 3: Determinazione del volume con l`altezza delle gambe

Immagine titolata Calculate the Volume of a Square Pyramid Step 10

1. Misura l`altezza delle gambe della piramide. L`altezza delle gambe è la lunghezza dei bordi della piramide, misurata dalla sommità a uno degli angoli della base. Come sopra, usa il teorema di Pitagora per calcolare l`altezza perpendicolare della piramide.

In questo esempio assumiamo che l`altezza delle gambe sia 11 cm e che l`altezza perpendicolare sia 5 cm.

Immagine titolata Calculate the Volume of a Square Pyramid Step 11

2. Immagina un triangolo rettangolo. Anche in questo caso è necessario un triangolo rettangolo per poter utilizzare il teorema di Pitagora. In questo caso, tuttavia, il valore sconosciuto è la base della piramide. Nota è l`altezza verticale e l`altezza delle gambe. Ora immagina di tagliare la piramide in diagonale da un angolo all`altro, quindi aprendo la figura, il piano risultante sembrerebbe un triangolo. L`altezza di quel triangolo è l`altezza perpendicolare della piramide. Questo divide il triangolo esposto in due triangoli rettangoli simmetrici. L`ipotenusa di ciascuno dei triangoli rettangoli è l`altezza delle gambe della piramide. La base di ciascuno dei triangoli rettangoli è metà della diagonale della base della piramide.

Immagine titolata Calculate the Volume of a Square Pyramid Step 12

3. Assegna variabili. Usa il triangolo rettangolo immaginario e assegna valori al Teorema di Pitagora. Conosci l`altezza verticale,

h,

$h,$ che è un lato del teorema di Pitagora,

un

$un$ . L`altezza delle gambe della piramide,

l,

$io,$ forma l`ipotenusa di questo triangolo rettangolo immaginario, e quindi ne prende il posto

C

$C$ . La diagonale sconosciuta della base della piramide è il lato rimanente del triangolo rettangolo,

B .

$B$ Dopo aver effettuato queste sostituzioni, l`equazione si presenta così:

un 2 + B^{2} = C^{2}

$a^{2}+b^{2}=c^{2}$

h 2 + B^{2} = l^{2}

$h^{2}+b^{2}=l^{2}$

Immagine titolata Calculate the Volume of a Square Pyramid Step 13

4. Calcola la diagonale della base quadrata. Devi riordinare l`equazione per ottenere la variabile

B

$B$ isolare, quindi calcolarne il valore.

h 2 + B^{2} = l^{2}

$h^{2}+b^{2}=l^{2}$ ..........(equazione aggiustata)

B 2 = l^{2} - h^{2}

$b^{2}=l^{2}-h^{2}$ ..........(sostituire h su entrambi i lati)

B = \sqrt{l} 2 - h^{2}

$b={sqrt{l^{2}-h^{2}}}$ ..........(sottrai la radice quadrata di entrambi i lati)

B = \sqrt{11} 2 - 5^{2}

$b={sqrt{11^{2}-5^{2}}}$ ..........(compilare i numeri)

B = \sqrt{121 - 25}

$b={sqrt{121-25}}$ ..........(semplificare i quadrati)

B = \sqrt{96}

$b={sqrt{96}}$ ..........(sottrai valori)

B = 9.80

$b=9,80$ ..........(semplificare la radice quadrata)

Raddoppia questo valore per trovare la diagonale della base quadrata della piramide. Pertanto, la diagonale della base della piramide è 9,8 * 2 = 19,6 cm.

Immagine titolata Calculate the Volume of a Square Pyramid Step 14

5. Trova il lato della base della diagonale. La base della piramide è un quadrato. La diagonale di ogni quadrato è uguale alla lunghezza di uno dei suoi lati, moltiplicata per radice quadrata 2. E quindi puoi trovare il lato di un quadrato dividendo la diagonale per la radice quadrata 2.

In questo esempio piramidale, la diagonale della base è 19,6 cm. Pertanto, il lato è uguale a:

S = \frac{19.6}{\sqrt{2}} = \frac{19.6}{1.41} = 13.90

$s={frac{19.6}{{sqrt{2}}}}={frac{19.6}{1.41}}=13.90$

Immagine titolata Calculate the Volume of a Square Pyramid Step 15

6. Calcola il volume usando il lato e l`altezza. Ritorna alla formula originale per calcolare il volume utilizzando l`altezza laterale e perpendicolare.

V = \frac{1}{3} S^{2} h

$V={frac{1}{3}}s^{2}h$

V = \frac{1}{3} {13.9}^{2} * 5

$V={frac{1}{3}}13,9^{2}*5$

V = \frac{1}{3} 193.23 * 5

$V={frac{1}{3}}193,23*5$

V = 322.02 centimetro 3

$V=322.02{testo{cm}}^{3}$

Consigli

In una piramide quadrata, l`altezza perpendicolare, l`apotema e la lunghezza del bordo della base possono essere calcolati utilizzando il teorema di Pitagora.