Trovare l'Area di una Piramide: 12 Passaggi (con Immagini)

Contenuto

Passi
- Metodo 1 di 2: Trovare l`Area di una Piramide Ordinaria
- Metodo 2 di 2: Trovare l`area di una piramide quadrata
Necessità

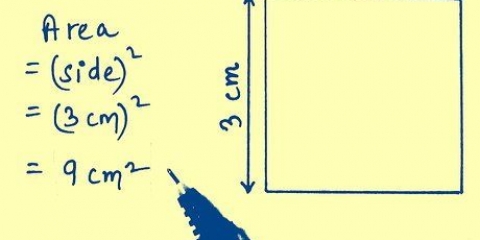
L`area di una piramide può essere trovata aggiungendo l`area della sua base all`area dei suoi lati. Quando lavori con le piramidi regolari puoi trovare l`area usando una formula purché tu sappia come trovare l`area della base della piramide. Poiché la base può essere un poligono, è utile sapere come determinare l`area di forme come pentagoni ed esagoni. Tuttavia, quando si lavora con la piramide quadrata regolare, calcolare l`area totale è facile, a condizione che si conosca l`altezza inclinata della piramide e la lunghezza della base quadrata.

Passi

Metodo 1 di 2: Trovare l`Area di una Piramide Ordinaria

Immagine titolata Trova la superficie di una piramide Step 1

1. Scrivi la formula per l`area di una piramide ordinaria. La formula è

S un = P \times h 2 + B

$SA={frac{ptimes h}{2}}+B$ , per cui

S un

$SA$ è uguale all`area totale della piramide,

P

$P$ è uguale al perimetro della base,

h

$h$ è uguale alla pendenza della piramide, e

B

$B$ è uguale all`area della base.

La formula base per l`area di una piramide, regolare o irregolare, è Area Totale = Area Base + Area Inclinata.
Non confondere `altezza inclinata` con `altezza.L`"altezza inclinata" è la distanza diagonale dalla sommità della piramide al bordo della base. L `"altezza" è la distanza perpendicolare dall`alto alla base.

Immagine titolata Trova la superficie di una piramide Step 2

2. Calcola il perimetro della base. Se il perimetro non è dato, ma è data la lunghezza di uno spigolo della base, puoi calcolare il perimetro moltiplicando la lunghezza di uno spigolo per il numero di spigoli.

Ad esempio, se vuoi trovare l`area di una piramide esagonale e sai che la lunghezza di uno spigolo della base è 4 cm, calcola

4 \times 6 = 24

$4volte 6=24$ per trovare il perimetro della base, perché un esagono ha sei lati. Quindi il perimetro della base è 24 cm, quindi la formula per l`area sarà simile a questa:

S un = 24 \times h 2 + B

$SA={frac{24times h}{2}}+B$ .

Immagine titolata Trova la superficie di una piramide Step 3

3. Immettere il valore dell`altezza della pendenza nella formula. Assicurati di utilizzare l`altezza inclinata, non l`altezza perpendicolare. L`altezza della pendenza dovrebbe essere indicata nel problema. Se non si conosce l`altezza della pendenza, non è possibile utilizzare questo metodo.

Supponiamo che l`altezza inclinata di una piramide esagonale sia 12 cm, quindi la tua formula sarà simile a questa:

S un = 24 \times 12 2 + B

$SA={frac{24volte 12}{2}}+B$ .

Immagine titolata Trova la superficie di una piramide Step 4

4. Calcola l`area della base. Il modo in cui lo fai dipende dalla forma della base. Per questo devi sapere come determinare le aree dei poligoni.

Ad esempio, se hai a che fare con una piramide esagonale, dovresti calcola l`area dell`esagono. La formula è

un = 3 \sqrt{3} \times S^{2} 2

$A={frac{3{sqrt{3}}times s^{{2}}}{2}}$ , per cui

S

$S$ è la lunghezza di un lato dell`esagono. Poiché la lunghezza di un lato dell`esagono è 4 cm, calcola come segue:

un = 3 \sqrt{3} \times 4^{2} 2

$A={frac{3{sqrt{3}}times 4^{{2}}}{2}}$

un = 3 \sqrt{3} \times 162

$A={frac{3{sqrt{3}}volte 16}{2}}$

un = 48 \sqrt{3} 2

$A={frac{48{sqrt{3}}}{2}}$

un = \frac{83.14}{2}

$A={frac{83,14}{2}}$

un = 41.57

$A=41,57$ .
Quindi l`area della base è di 41,57 centimetri quadrati.

Immagine titolata Trova la superficie di una piramide Step 5

5. Applicare l`area della base alla formula. Assicurati di avere la variabile

B

$B$ sostituisce.

Supponiamo che l`area della base esagonale sia 41,57 cm. quindi la tua formula per l`area sarebbe simile a questa:

S un = 24 \times 12 2 + 41.57

$SA={frac{24times 12}{2}}+41.57$ .

Immagine titolata Trova la superficie di una piramide Step 6

6. Moltiplica il perimetro della base per l`altezza inclinata della piramide. Dividi il prodotto per due. Questo ti dà l`area inclinata delle facce della piramide.

Ad esempio:

S un = 24 \times 12 2 + 41.57

$SA={frac{24times 12}{2}}+41.57$

S un = \frac{288}{2} + 41.57

$SA={frac{288}{2}}+41.57$

S un = 144 + 41.57

$SA=144+41.57$

Immagine titolata Trova la superficie di una piramide Step 7

7. Somma i due valori insieme. La somma è l`area inclinata più l`area di base, quindi ottieni l`area totale della piramide in unità quadrate.

Ad esempio:

S un = 144 + 41, 57

$SA=144+41.57$

S un = 185, 57

$SA=185,57$
Quindi l`area totale di una piramide esagonale, con una data lunghezza del bordo di base di 4 cm e un`altezza del pendio di 12 cm, è pari a 185,57 centimetri quadrati.

Metodo 2 di 2: Trovare l`area di una piramide quadrata

Immagine titolata Trova la superficie di una piramide Step 8

1. Scrivi la formula per l`area di una piramide quadrata. La formula è

S un = B 2 + 4 (B h 2)

$SA=b^{{2}}+4({frac{bh}{2}})$ , per cui

B

$B$ è uguale alla lunghezza di un lato della base, e

h

$h$ è uguale alla pendenza della piramide.

Non confondere `altezza inclinata` con `altezza.L`"altezza inclinata" è la distanza diagonale dalla sommità della piramide al bordo della base. L `"altezza" è la distanza perpendicolare dalla cima alla base.
Nota che questa formula è solo un altro modo per calcolare Area totale = Area di base ( $B 2$ $b^{{2}}$ ) + Superficie inclinata ( $4 (B h 2)$ $4({frac{bh}{2}})$ ) scrivere. Questa formula funziona solo per piramidi quadrate regolari.

Immagine titolata Trova la superficie di una piramide Step 9

2. Immettere nella formula i valori della lunghezza dei lati e dell`altezza della pendenza. Assicurati di sostituire la lunghezza del lato della base con

B

$B$ e l`altezza inclinata di

h

$h$ .

Supponiamo che la lunghezza di un lato della base di una piramide quadrata sia 4 cm e l`altezza della pendenza sia 12 cm, quindi la formula sarebbe simile a questa:

S un = 4 2 + 4 ((4) (12) 2)

$SA=4^{{2}}+4({frac{(4)(12)}{2}})$ .

Immagine titolata Trova la superficie di una piramide Step 10

3. Riquadra la lunghezza di un lato della base. Questo ti darà l`area della base.

Ad esempio:

S un = 4 2 + 4 ((4) (12) 2)

$SA=4^{{2}}+4({frac{(4)(12)}{2}})$

S un = 16 + 4 ((4) (12) 2)

$SA=16+4({frac{(4)(12)}{2}})$

Immagine titolata Trova la superficie di una piramide Step 11

4. Moltiplica la lunghezza di un lato della base per l`altezza della pendenza e dividi per due. Quindi moltiplica per quattro. Questo ti darà la superficie angolata della piramide.

Ad esempio: