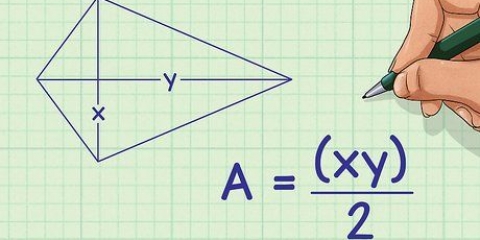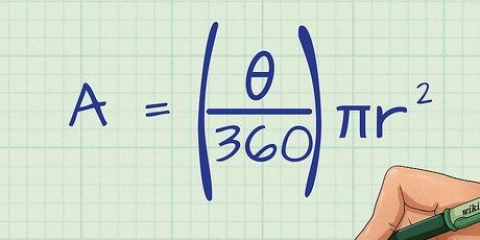Come Calcolare l'Area di un Triangolo Isoscele (con Immagini)

Contenuto

Passi
- Metodo 1 di 2: Determinazione dell`area utilizzando le lunghezze di ciascun lato
- Metodo 2 di 2: utilizzo della trigonometria
Consigli

Un triangolo isoscele è un triangolo con due lati della stessa lunghezza. Questi due lati uguali hanno sempre lo stesso angolo rispetto alla base (il terzo lato) e si incontrano direttamente sopra il centro della base. Puoi provarlo tu stesso con un righello e due matite della stessa lunghezza: se provi a inclinare il triangolo in una direzione, le estremità delle matite non si incontreranno. Con queste proprietà speciali del triangolo isoscele, l`area può essere calcolata con pochi dati.

Passi

Metodo 1 di 2: Determinazione dell`area utilizzando le lunghezze di ciascun lato

Immagine titolata Trova l`area di un triangolo isoscele Passaggio 1

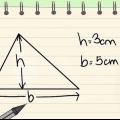
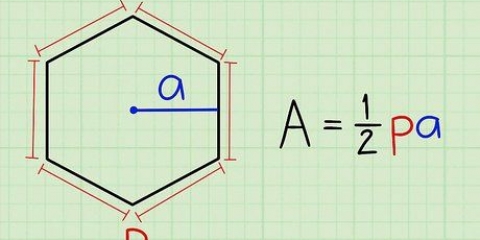
1. Prendi l`area di un parallelogramma. Quadrati e rettangoli sono parallelogrammi, come qualsiasi forma a quattro lati in cui due coppie di lati sono parallele tra loro. Tutti i parallelogrammi hanno una semplice formula dell`area: l`area è uguale alla base moltiplicata per l`altezza, o A = bh. Se metti un parallelogramma immaginario in posizione verticale su una superficie orizzontale, la base è la lunghezza del lato su cui si trova la figura. L`altezza è la distanza dalla base al punto più alto (come ci si aspetterebbe); cioè la distanza dalla base al lato opposto. Misurare sempre l`altezza ad angolo retto (90 gradi) rispetto alla base.

Per quadrati e rettangoli, l`altezza è uguale alla lunghezza di un lato verticale, poiché questi lati sono ad angolo retto rispetto al suolo.

Immagine titolata Trova l`area di un triangolo isoscele Step 2

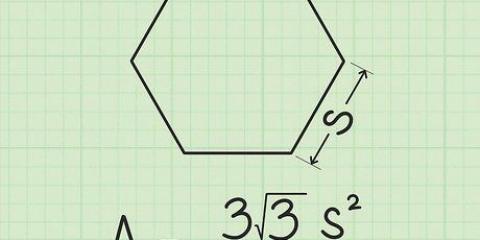
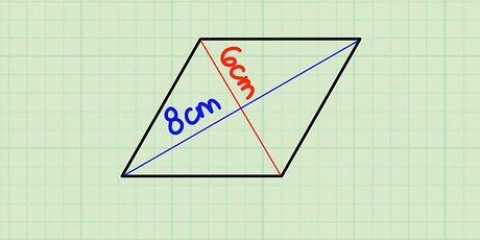
2. Confronta Triangoli e Parallelogrammi. C`è una semplice relazione tra queste due forme. Tagliare un parallelogramma a metà lungo la diagonale lo divide in due triangoli uguali. Allo stesso modo, puoi unire due triangoli identici per formare un parallelogramma. Ciò significa che l`area di un triangolo può essere scritta come A = bh, esattamente la metà di un parallelogramma corrispondente.

Immagine titolata Trova l`area di un triangolo isoscele Step 3

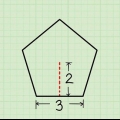
3. Trova la base del triangolo isoscele. Ora hai la formula, ma cosa sono esattamente la "base" e l` "altezza" di un triangolo isoscele? La base è la parte facile: prendi il terzo lato disuguale del triangolo isoscele.

Ad esempio, se un triangolo isoscele ha i lati di 5 cm, 5 cm e 6 cm, allora il lato di 6 cm è la base.

Se un triangolo ha tre lati uguali (ed è quindi equilatero), puoi scegliere qualsiasi lato come base. Un triangolo equilatero è un tipo speciale di triangolo isoscele, ma puoi trovare la sua area allo stesso modo.

Immagine titolata Trova l`area di un triangolo isoscele Step 4

4. Disegna una linea tra la base e il vertice opposto. Assicurati che la linea tocchi la base ad angolo retto. La lunghezza di questa linea è l`altezza del triangolo ed è quindi etichettata h. Una volta ottenuto il valore di h calcolato, è possibile determinare l`area.

In un triangolo isoscele, questa linea tocca sempre la base nel suo centro esatto.

Immagine titolata Trova l`area di un triangolo isoscele Step 5

5. Visualizza una metà del triangolo isoscele. Si noti che l`altitudine divide il triangolo isoscele in due triangoli rettangoli identici. Guarda uno di loro e indica i tre lati:

Uno dei lati corti è uguale alla metà della base:

\frac{B}{2}

${frac{b}{2}}$ .

L`altro lato corto è l`altezza h.

L`ipotenusa (ipotenusa) del triangolo rettangolo è uno dei due lati uguali del triangolo isoscele. Prendiamo questo S menzionare.

Immagine titolata Trova l`area di un triangolo isoscele Step 6

6.Usa il teorema di Pitagora. Se conosci due lati di un triangolo rettangolo e vuoi trovare il terzo, puoi usare il Teorema di Pitagora: (lato 1) + (lato 2) = (ipotenusa) Sostituisci le variabili che usiamo in questo problema e ottieni

(\frac{B}{2})^{2} + h^{2} = S^{2}

$({frac{b}{2}})^{2}+h^{2}=s^{2}$ .

Probabilmente hai imparato il teorema di Pitagora se

un 2 + B^{2} = C^{2}

$a^{2}+b^{2}=c^{2}$ . Scrivere questo come "lati" e "ipotenusa" ti evita di confonderli con le variabili del triangolo.

Immagine titolata Trova l`area di un triangolo isoscele Step 7

7. Risolvere per h. Ricorda che hai la formula dell`area B e h usato, ma di cui non si conosce il valore h non lo so ancora. Riscrivi la formula h risolvere:

(\frac{B}{2})^{2} + h^{2} = S^{2}

$({frac{b}{2}})^{2}+h^{2}=s^{2}$

h 2 = S^{2} - (\frac{B}{2})^{2}

$h^{2}=s^{2}-({frac{b}{2}})^{2}$

h = \sqrt{(} S^{2} - (\frac{B}{2})^{2})

$h={sqrt(}s^{2}-({frac{b}{2}})^{2})$ .

Immagine titolata Trova l`area di un triangolo isoscele Step 8

8. Sostituisci i valori del tuo triangolo con h Ora che conosci questa formula, puoi usarla per un triangolo isoscele di cui conosci i lati. Basta inserire la lunghezza della base per B e la lunghezza di uno dei lati uguali per S, e poi calcola h.

Ad esempio, hai un triangolo isoscele con i lati 5 cm, 5 cm e 6 cm. B = 6 e S = 5.

Usa questi valori nella tua formula:

h = \sqrt{(} S^{2} - (\frac{B}{2})^{2})

$h={sqrt(}s^{2}-({frac{b}{2}})^{2})$

h = \sqrt{(} 5^{2} - (\frac{6}{2})^{2})

$h={sqrt(}5^{2}-({frac{6}{2}})^{2})$

h = \sqrt{(} 25 - 3^{2})

$h={sqrt(}25-3^{2})$

h = \sqrt{(} 25 - 9)

$h={sqrt(}25-9)$

h = \sqrt{(} 16)

$h={sqrt(}16)$

h = 4

$h=4$ centimetro.

Immagine titolata Trova l`area di un triangolo isoscele Step 9

9. Usa i valori di base e altezza nella formula dell`area. Ora hai quello che ti serve per usare la formula dall`inizio di questa sezione: Area = ½bh. Sostituisci i valori per b e h in questa formula e calcola la risposta. Non dimenticare di scrivere la tua risposta in unità quadrate.

Per continuare con l`esempio: il triangolo 5-5-6 ha una base di 6 cm e un`altezza di 4 cm.

A = bh
A = ½(6 cm)(4 cm)
A = 12 cm.

Immagine titolata Trova l`area di un triangolo isoscele Step 10

10. Prova un esempio più difficile. La maggior parte dei triangoli isoscele sono più difficili da lavorare rispetto all`esempio precedente. L`altezza contiene spesso una radice quadrata che non può essere semplificata a un numero intero. Se questo è il caso, lasciare l`altezza come radice quadrata nel la forma più semplice Stare in piedi. Ecco un esempio:

Qual è l`area di un triangolo con i lati 8 cm, 8 cm e 4 cm?

Il lato irregolare è di 4 cm e la base B.

L`altezza

h = \sqrt{8} 2 - (\frac{4}{2})^{2}

$h={sqrt{8^{2}-({frac{4}{2}})^{2}}}$

= \sqrt{64 - 4}

$={sqrt{64-4}}$

= \sqrt{60}

$={sqrt{60}}$

Semplifica la radice quadrata calcolando:

h = \sqrt{60} = \sqrt{4 * 15} = \sqrt{4} \sqrt{15} = 2 \sqrt{15} .

$h={sqrt{60}}={sqrt{4*15}}={sqrt{4}}{sqrt{15}}=2{sqrt{15}}$

Superficie

= \frac{1}{2} B h

$={frac{1}{2}}bh$

= \frac{1}{2} (4) (2 \sqrt{15})

$={frac{1}{2}}(4)(2{sqrt{15}})$

= 4 \sqrt{15}

$=4{sqrt{15}}$

Lascia questa risposta come annotata o usa una calcolatrice per una stima decimale (circa 15,49 cm2).

Metodo 2 di 2: utilizzo della trigonometria

Immagine titolata Trova l`area di un triangolo isoscele Step 11

1. Inizia con un lato e un angolo. Se hai familiarità con la trigonometria, puoi trovare l`area di un triangolo isoscele anche se nessuna delle lunghezze dei suoi lati è nota. Ecco un problema di esempio in cui è noto solo quanto segue:

La lunghezza S dei due lati uguali è 10 cm.
L`angolo θ tra i due lati uguali è di 120 gradi.

Immagine titolata Trova l`area di un triangolo isoscele Step 12

2. Dividi il triangolo isoscele in due triangoli rettangoli. Traccia una linea dal vertice tra i due lati uguali, intersecando la base ad angolo retto. Ora hai due triangoli rettangoli uguali.

Questa linea divide θ perfettamente a metà. Ogni triangolo rettangolo ha un angolo di ½θ, o in questo caso (½)(120) = 60 gradi.

Immagine titolata Trova l`area di un triangolo isoscele Step 13

3. Utilizzare la trigonometria per determinare il valore di h. Ora che hai un triangolo rettangolo, puoi applicare le funzioni trigonometriche (seno, coseno e tangente). Nel problema di esempio sai qual è l`ipotenusa e vuoi il valore di h sai, il lato vicino all`angolo noto. Usa il fatto che coseno = adiacente / ipotenusa a h risolvere:

cos(θ/2) = h / s

cos(60º) = h / 10

h = 10 cos(60º)

Immagine titolata Trova l`area di un triangolo isoscele Step 14

4. Determina il valore del lato rimanente. C`è un lato ancora sconosciuto del triangolo rettangolo, che tu X può nominare. Risolvi questo con la definizione seno = opposto / ipotenusa:

sin(θ/2) = x / s

sin(60º) = x / 10

x = 10peccato(60º)

Immagine titolata Trova l`area di un triangolo isoscele Step 15

5. Usa la relazione di x con la base del triangolo isoscele. Ora puoi "rimpicciolire" il triangolo isoscele in questione. La base B di quell`angolo è uguale a 2X, poiché era diviso in due segmenti, ciascuno con una lunghezza X.

Immagine titolata Trova l`area di un triangolo isoscele Step 16

6. Usa i valori h e B nella formula dell`area per il triangolo. Ora che conosci la base e l`altezza, puoi applicare la formula standard A = ½bh:

un = \frac{1}{2} B h

$A={frac{1}{2}}bh$

= \frac{1}{2} (2 X) (10 C o S 60)

$={frac{1}{2}}(2x)(10cos60)$

= (10 S io n 60) (10 C o S 60)

$=(10sin60)(10cos60)$

= 100 S io n (60) C o S (60)

$=100peccato(60)cos(60)$

Usando una calcolatrice (impostata in gradi), ottieni circa 43,3 cm2 come risposta. In alternativa, usa le proprietà della trigonometria per semplificarle in A = 50sin(1200).

Immagine titolata Trova l`area di un triangolo isoscele Step 17

7. Riscrivilo come una formula universale. Ora che sai come risolvere questo problema, puoi applicare la formula generale senza eseguire l`intero processo ogni volta. Ecco cosa ottieni se ripeti questo processo, senza utilizzare valori specifici (e semplificando usando le proprietà della trigonometria):

un = \frac{1}{2} S^{2} S io n θ

$A={frac{1}{2}}s^{2}peccatoteta$

s è la lunghezza di uno dei due lati uguali.

Θ è l`angolo tra i due lati uguali.

Consigli

Se hai a che fare con un triangolo rettangolo isoscele (due lati uguali e un angolo di 90 gradi), è molto più facile trovare l`area. Se usi uno dei lati corti come base, l`altro lato corto è l`altezza. Ora la formula A = ½ b * h può essere semplificata a ½s, dove s è la lunghezza di un lato corto.
Le radici quadrate hanno due soluzioni, una positiva e una negativa, ma puoi ignorare il negativo in geometria. Ad esempio, non puoi avere un triangolo con `altezza negativa`.
Alcuni problemi trigonometrici ti danno altre informazioni da cui partire, come la lunghezza della base e un angolo (e il fatto che il triangolo è isoscele). La strategia di base rimane la stessa: dividere il triangolo isoscele in triangoli rettangoli e calcolarli per altezza, usando le funzioni trigonometriche.

Articoli sull'argomento "Calcola l'area di un triangolo isoscele"

Calcola l'area di un quadrilatero

Calcola l'area di un pentagono

Calcola l'area di un triangolo

Calcola area

Condividi sui social network: