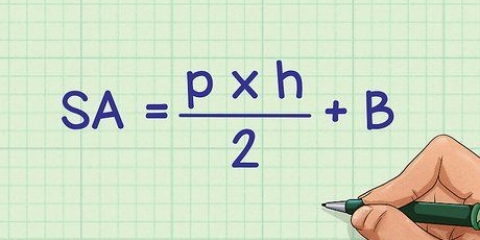Registra questa misurazione come un. Esempio: a = 2 cm 
Nota che questo passaggio calcola l`area di una faccia del cubo. Esempio: a = 2 cm a = 2 x 2 = 4 cm 
Questo passaggio completa il calcolo dell`area del cubo. Esempio: a = 4 cm Area = 6 x a = 6 x 4 = 24 cm 

Misurare la lunghezza della base per determinare la lunghezza del prisma e assegnarla a C. Esempio: c = 5 cm Misura la larghezza della base per determinare la larghezza del prisma e chiamala un. Esempio: a = 2 cm Misurare l`altezza del lato per determinare l`altezza del prisma e chiamarla B. Esempio: b = 3 cm 
Esempio: 2 x (a x c) = 2 x (2 x 5) = 2 x 10 = 20 cm 
Esempio: 2 x (a x b) = 2 x (2 x 3) = 2 x 6 = 12 cm 
Esempio: 2 x (b x c) = 2 x (3 x 5) = 2 x 15 = 30 cm 
Esempio: Area = 2ab + 2bc + 2ac = 12 + 30 + 20 = 62 cm. 

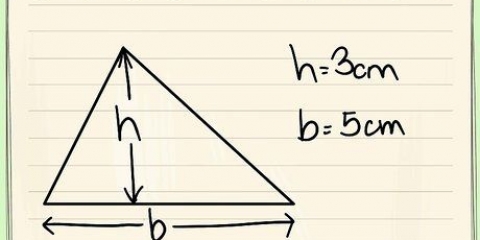
La base B, è uguale alla lunghezza della parte inferiore del triangolo. Esempio: b = 4 cm L`altezza h della base triangolare è uguale alla distanza tra il bordo inferiore e la punta. Esempio: h = 3 cm L`area di un triangolo moltiplicata per 2 = 2(1/2)b*h = b*h = 4*3 =12 cm 
Esempio: H = 5 cm I tre lati si riferiscono ai tre lati della base triangolare. Esempio: S1 = 2 cm, S2 = 4 cm, S3 = 6 cm 
Esempio: P = S1 + S2 + S3 = 2 + 4 + 6 = 12 cm 
Esempio: P x A = 12 x 5 = 60 cm 
Esempio: 2A + PH = 12 + 60 = 72 cm. 

Esempio: r = 3 cm 
Esempio: r = r x r = 3 x 3 = 9 cm 
Esempio: π*r = 3,14 x 9 = 28,26 cm 
Esempio: 4π*r = 4 x 28,26 = 113,04 cm 

Esempio: r = 3 cm Esempio: h = 5 cm 
Esempio: Area della base = π*r = 3,14 x 3 x 3 = 28,26 cm Esempio: 2π*r = 2 x 28,26 = 56,52 cm 
Esempio: 2π*dx = 2 x 3,14 x 3 x 5 = 94,2 cm 
Esempio: 2π*r + 2π*rh = 56,52 + 94,2 = 150,72 cm 

Esempio: l = 3 cm Esempio: s = 1 cm 
Esempio: s = s x s = 1 x 1 = 1 cm 
Esempio: 2 x s x l = 2 x 1 x 3 = 6 cm 
Esempio: s + 2sl = 1 + 6 = 7 cm 

Esempio: r = 2 cm Esempio: h = 4 cm 
Esempio: l = √ (r + h) = √ (2 x 2 + 4 x 4) = √ (4 + 16) = √ (20) = 4,47 cm 
Esempio: π*r = 3,14 x 2 x 2 = 12,56 cm 
Esempio: π*rl = 3,14 x 2 x 4,47 = 28,07 cm 
Esempio: π*r + π*rl = 12,56 + 28,07 = 40,63 cm
Calcola area
Contenuto
L`area è lo spazio totale occupato da tutte le aree di un oggetto. È la somma di tutte le aree di quell`oggetto. Determinare l`area di una forma tridimensionale è abbastanza facile, a patto di utilizzare la formula giusta. Ogni forma ha la sua formula separata, quindi dovrai prima controllare quale forma è. Il calcolo della formula dell`area per vari oggetti può semplificare i calcoli in futuro. Qui discutiamo alcune delle forme più comuni che potresti incontrare.
Passi
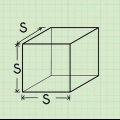
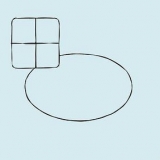
Metodo 1 di 7: Cubo

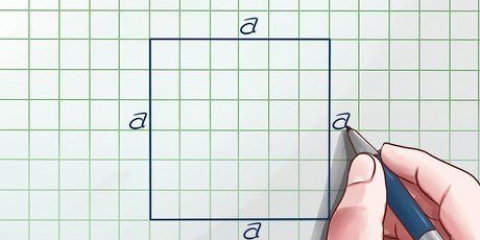
1. Definisci la formula per l`area di un cubo. Un cubo ha sei facce identiche. Poiché sia la lunghezza che la larghezza di un quadrato sono uguali, l`area di un quadrato lo è un, per cui un la lunghezza è un lato. Poiché un cubo ha sei facce uguali, puoi calcolarne l`area moltiplicando l`area di una delle sue facce per sei. La formula per l`area di un cubo O è O = 6a, per cui un la lunghezza è un lato.
- L`unità di area è una certa lunghezza al quadrato: cm, dm, m, ecc.

2. Misura la lunghezza di un lato. Per definizione, ogni lato o bordo (bordo) di un cubo dovrebbe essere uguale all`altro, quindi devi misurare solo un lato. Misura la lunghezza del lato con un righello. Presta attenzione alle unità che usi.

3. Squadra la tua misura per un. Al quadrato la misura per calcolare la lunghezza della nervatura. Quadrare un valore significa moltiplicarlo per se stesso. Se stai imparando questo per la prima volta, potrebbe essere utile ricordarlo come NT= 6*a*a.

4. Moltiplica questo prodotto per sei. Ricorda che un cubo ha sei facce identiche. Ora che conosci l`area di una delle facce, moltiplicala per sei (a causa di tutte e sei le facce).
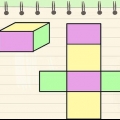
Metodo 2 di 7: Prisma rettangolare

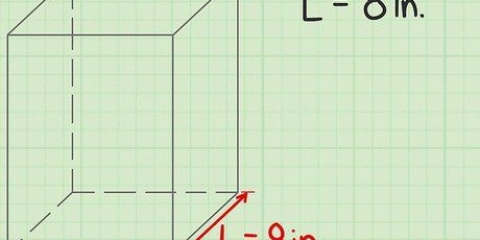
1. Definisci la formula per l`area di un prisma rettangolare. Come un cubo, un prisma rettangolare ha sei facce, ma a differenza di un cubo, quelle facce non sono uguali. In un prisma rettangolare, solo le facce opposte sono uguali tra loro. Pertanto, quando si calcola l`area di un prisma rettangolare, bisogna tenere conto delle varie lunghezze delle nervature, come nella formula SA = 2ab + 2bc + 2ac.
- Per questa formula, un uguale alla larghezza del prisma, B uguale all`altezza e C uguale alla lunghezza.
- Se osserviamo più da vicino la formula, vedrai che sommiamo semplicemente tutte le aree di ciascuna faccia dell`oggetto.
- L`unità di area sarà una certa lunghezza al quadrato: cm, dm, m, ecc.

2. Misura la lunghezza, l`altezza e la larghezza di ciascun lato. Tutte e tre le letture possono essere diverse, quindi ciascuna deve essere misurata separatamente. Misura ogni lato con un righello e annota il valore. Usa le stesse unità per ogni misura.

3. Calcola l`area di una delle facce del prisma e moltiplicala per due. Ricorda che ci sono sei facce in un prisma rettangolare e le facce opposte sono uguali tra loro. Moltiplica la lunghezza e l`altezza, o C e un, per trovare l`area di un aereo. Prendi questa misura e moltiplicala per due per tenere conto del piano identico opposto.

4. Trova l`area dell`altra faccia del prisma e moltiplicala per due. Come per il primo insieme di facce, moltiplicare la larghezza e l`altezza, o un e B per determinare l`area di un`altra faccia del prisma. Moltiplica questa misura per due per tenere conto dei lati identici opposti.

5. Calcola l`area delle estremità del prisma e moltiplicala per due. Le altre due facce del prisma sono le estremità. Moltiplica la lunghezza e la larghezza (C e B) per trovare la loro superficie. Moltiplica quest`area per due per tenere conto di entrambi i lati.

6. Aggiungi le tre aree separate insieme. Poiché l`area del prisma è l`area totale di tutte le facce di un oggetto, l`ultimo passaggio consiste nel sommare tutte le aree calcolate individualmente. Aggiungi le aree di tutti i lati insieme per ottenere l`area totale.
Metodo 3 di 7: Prisma triangolare

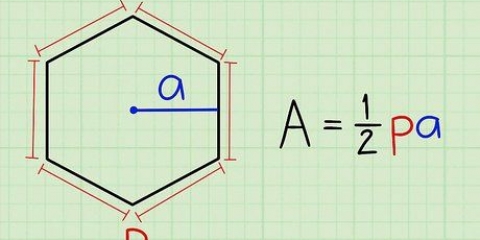
1. Definire la formula dell`area per un prisma triangolare. Un prisma triangolare ha due facce triangolari identiche e tre facce rettangolari. Per trovare l`area, devi calcolare l`area di tutte le facce e sommarle. L`area di un prisma triangolare è SA = 2A + PH, dove A è l`area della base triangolare, P è il perimetro della base triangolare e h è l`altezza del prisma.
- Per questa formula vale un il area di un triangolo e quindi LA = 1/2 bh, per cui B è la base del triangolo e h l`altezza.
- P è il perimetro del triangolo calcolato sommando tutti e tre gli spigoli del triangolo.
- L`unità di area è un`unità di lunghezza al quadrato: cm, dm, m, ecc.

2. Calcola l`area del piano triangolare e moltiplicalo per due. L`area di un triangolo è /2b*h dove b è la base del triangolo e h è l`altezza. Quindi, poiché ci sono due triangoli identici come facce, moltiplichiamo la formula per due. Questo rende facile il calcolo per entrambi i piani (b*h).

3. Misura ogni lato del triangolo e l`altezza del prisma. Per completare il calcolo dell`area, è necessario conoscere la lunghezza di ciascun lato del triangolo e l`altezza del prisma. L`altezza è la distanza tra le due facce triangolari.

4. Trova il perimetro del triangolo. Il perimetro del triangolo può essere calcolato sommando tutti i lati misurati: S1 + S2 + S3.

5. Moltiplica la circonferenza della base per l`altezza del prisma. Ricorda che l`altezza del prisma è la distanza tra le due facce triangolari. In altre parole, moltiplicare P di eh.

6. Somma le due letture separate insieme. È necessario sommare le due misurazioni dei due passaggi precedenti per ottenere l`area del prisma triangolare.
Metodo 4 di 7: Bol

1. Definire la formula dell`area per una sfera. Una sfera ha una superficie curva, quindi l`area della superficie è un valore moltiplicato per la costante, pi. L`area di una sfera viene calcolata utilizzando l`equazione NT = 4π*r.
- Per questa formula, R uguale al raggio della sfera. Pi (o π) può essere arrotondato a 3,14.
- Le unità dell`area saranno un`unità di lunghezza, al quadrato: cm, dm, m, ecc.

2.Misura il raggio del bulbo. Il raggio della sfera è la metà del diametro, ovvero la distanza dal centro della sfera al bordo.

3. Al quadrato il raggio. Per quadrare un numero, moltiplicalo per se stesso. Moltiplica la misura per R con se stesso. Ricorda che questa formula può essere riscritta come SA = 4π*r*r.

4. Moltiplica il raggio al quadrato per un arrotondamento di pi. Pi è una costante che rappresenta il rapporto tra la circonferenza di un cerchio e il suo diametro. È un numero irrazionale con molte cifre dopo la virgola. Viene spesso arrotondato a 3,14. Moltiplica il raggio al quadrato per π, o 3,14, per l`area di una sezione trasversale circolare della sfera.

5. Moltiplica questo prodotto per quattro. Per completare il calcolo, moltiplicalo per quattro. Trova l`area della sfera moltiplicando l`area circolare piatta per quattro.
Metodo 5 di 7: Cilindro

1. Definire la formula dell`area per un cilindro. Un cilindro ha due estremità circolari che chiudono una superficie tubolare. La formula per l`area di un cilindro è NT = 2π*r + 2π*rh, per cui R è uguale al raggio della base circolare e h è uguale all`altezza del cilindro. il giro pi (o π) diminuisce a 3,14.
- La formula 2π*r calcola l`area delle due estremità circolari, mentre 2πrh è l`area della colonna tra le due estremità.
- Le unità di area sono un`unità di lunghezza al quadrato: cm, dm, m, ecc.

2. Misurare il raggio e l`altezza del cilindro. Il raggio di un cerchio è la metà del suo diametro, ovvero la distanza dal centro del cerchio al bordo. L`altezza è la distanza totale del cilindro da un`estremità all`altra. Disegna queste misure con un righello e scrivile.

3. Trova l`area della base e moltiplicala per due. Per trovare l`area della base, usa la formula dell`area o un cerchio (π*r). Per completare il calcolo, quadra il raggio e moltiplicalo per pi. Quindi moltiplica per due a causa del secondo cerchio identico all`altra estremità del cilindro.

4. Calcola la superficie del cilindro stesso con 2π*rh. Questa è la formula per calcolare l`area di un tubo. Il tubo è lo spazio tra le due estremità circolari del cilindro. Moltiplica il raggio per due, pi e l`altezza.

5. Somma le due letture separate insieme. Aggiungi l`area dei due cerchi all`area dello spazio tra i due cerchi per calcolare l`area totale del cilindro. Nota: aggiungendo questi due pezzi riconosci la formula originale: NT =2π*r + 2π*rh.
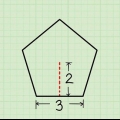
Metodo 6 di 7: Piramide Quadrata

1. Definire la formula dell`area per una piramide quadrata. Una piramide quadrata ha una base quadrata e quattro lati triangolari. Come accennato, l`area di un quadrato è la lunghezza di un lato al quadrato. L`area di un triangolo è 1/2 sl (il lato del triangolo moltiplicato per la lunghezza o l`altezza del triangolo). Poiché ci sono quattro triangoli, calcoli l`area totale moltiplicandola per quattro. Sommando tutte queste facce insieme si ottiene l`equazione dell`area per una piramide quadrata: NT = s + 2ch.
- In questa equazione, S la lunghezza di ciascun lato della base quadrata e l l`altezza inclinata di ciascun lato triangolare.
- L`unità di area è una certa unità di lunghezza al quadrato: cm, dm, m, ecc.

2. Misurare l`altezza inclinata e il lato della base. L`altezza obliqua l, è l`altezza di uno dei lati triangolari. È la distanza dalla base alla punta della piramide, misurata lungo un lato piatto. Il lato fondamentale S, è la lunghezza di un lato della base quadrata. Poiché la base è quadrata, questa misura è la stessa per tutti i lati. Usa un righello per ogni misura.

3. Trova l`area della base quadrata. L`area di una base quadrata può essere calcolata quadrando la lunghezza di un lato (S moltiplicare per se stesso).

4. Calcola l`area totale delle quattro facce triangolari. La seconda parte dell`equazione è l`area delle restanti quattro facce triangolari. Usando la formula 2ls, moltiplichiamo S di l e due. Trova l`area di ciascuna faccia.

5. Aggiungi le due aree separate insieme. Aggiungi l`area totale delle facce all`area della base per calcolare l`area totale.
Metodo 7 di 7: Cono

1. Definire la formula dell`area per un cono. Un cono ha una base circolare e una superficie rotonda che si assottiglia in un punto. Per trovare l`area, prendi l`area della base circolare e l`area del cono e aggiungi le due insieme. La formula per l`area di un cono è: SA = π*r + π*rl, per cui R il raggio è dalla base circolare, l l`altezza obliqua del cono, e π è la costante pi (3.14).
- L`unità di area è una certa unità di lunghezza al quadrato: cm, dm, m, ecc.

2. Misurare il raggio e l`altezza del cono. Il raggio è la distanza dal centro della base circolare al bordo della base. L`altezza è la distanza dal centro della base alla punta del cono, misurata attraverso il centro del cono.

3. Calcola l`altezza del pendio (l) del cono. Poiché l`altezza obliqua è l`effettiva ipotenusa di un triangolo, è necessario trovare il usando il teorema di Pitagora per calcolarlo. Usa la forma riorganizzata, l = √ (r + h), per cui R il raggio è e h l`altezza del cono.

4. Trova l`area della base circolare. L`area della base si calcola con la formula π*r. Dopo aver misurato il raggio, lo quadra (quindi lo moltiplichi per se stesso) e poi moltiplichi quel prodotto per pi greco.

5. Calcola l`area della sommità del cono. Usa la formula π*rl, dove R il raggio è del cerchio e l la pendenza come calcolato sopra, per determinare l`area della sommità del cono.

6. Aggiungi le due aree insieme per ottenere l`area totale del cono. Calcola l`area finale del cono aggiungendo l`area della base circolare durante il calcolo del passaggio precedente.
Necessità
- Governate
- Penna o matita
- Carta
Articoli sull'argomento "Calcola area"
Condividi sui social network:
Popolare