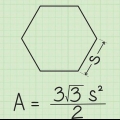
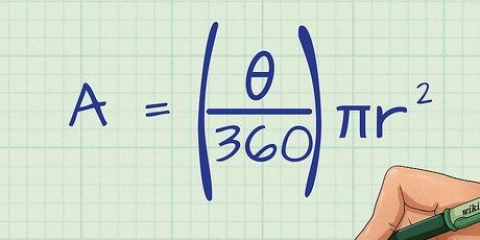Vedi l`apotema come il "x√3"-lato di un triangolo 30-60-90. Puoi vederlo in questo modo perché l`esagono è composto da sei triangoli equilateri. L`apotema taglia a metà uno di questi triangoli, creando un triangolo con angoli di 30, 60 e 90 gradi. Sai che il lato opposto all`angolo di 60 gradi ha una lunghezza di x√3, il lato opposto all`angolo di 30 gradi ha una lunghezza di x e il lato opposto all`angolo di 90 gradi ha una lunghezza di 2x. Se 10√3 sta per "x√3," allora sai che x = 10. Sai che x è la metà della lunghezza della parte inferiore del triangolo. Raddoppia per determinare la lunghezza totale. Quindi la parte inferiore del triangolo è 20. Ci sono sei di questi lati nell`esagono, quindi per trovare il perimetro dell`esagono moltiplichiamo 20 per 6 = 120. 
Area = 1/2 x 120 x 10√3 Area = 60 x 10√3 Area = 600√3 


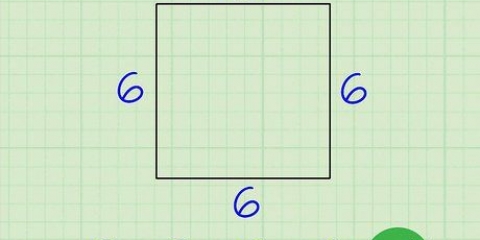
Se hai un quadrato con i lati di lunghezza 6, l`area è 6 x 6 = 36. 
Se la base di un rettangolo è 4 e l`altezza è 3, l`area è 4 x 3 = 12. 
Supponiamo di avere un trapezio le cui basi hanno lunghezza 6 e 8 e la cui altezza è 10. Quindi l`area è [(6 + 8) x 10]/2, che può essere semplificata in (14 x 10)/2 o 140/2, che è un`area di 70. 





Calcola l'area di un poligono
Contenuto
Calcolare l`area di un poligono può essere molto semplice quando si tratta di un triangolo regolare. Ma diventa molto più difficile quando si tratta di una forma irregolare con undici lati. Se vuoi sapere come calcolare l`area di diversi poligoni, segui questi passaggi.
Passi
Parte 1 di 3: Calcolo dell`area dei poligoni usando l`apotema

1. Scrivi la formula per trovare l`area di un poligono regolare. Per trovare l`area di un poligono regolare, tutto ciò che devi fare è seguire la formula: area = 1/2 x perimetro x apotema. Ciò significa quanto segue:
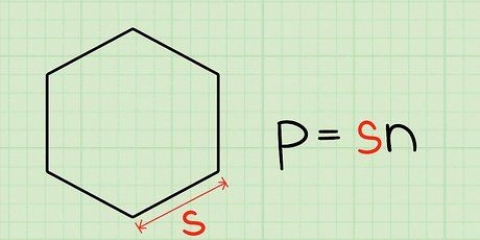
- Circonferenza = la somma delle lunghezze di tutti i lati
- Apotema = il segmento e anche la distanza dal centro del poligono al centro di un lato

2. Determina l`apotema del poligono. Se usi il metodo dell`apotema, l`apotema sarà sempre scontato. Supponiamo di lavorare con un esagono il cui apotema ha una lunghezza di 10√3.

3. Determina il perimetro del poligono. Se la circonferenza è scontata, hai quasi finito. Ma probabilmente solo l`apotema è scontato. Se sai che è un poligono regolare, puoi usare l`apotema per determinarne il perimetro. Ecco come lo fai:

4. Ora possiamo mettere l`apotema e il perimetro nella formula. Di nuovo: area = 1/2 x perimetro x apotema, il perimetro è 120 e l`apotema è 10√3. Allora la formula si presenta così:

5. Semplifica la tua risposta. Forse dovresti scrivere il risultato in decimali anziché in un radicale. Usa la calcolatrice per trovare la radice quadrata approssimativa di tre e moltiplicala per 600. √3 x 600 = 1.039.2. Questo è il risultato in decimali.
Parte 2 di 3: Trovare l`area di un poligono regolare usando altre formule

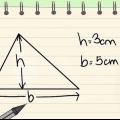
1. Calcola l`area di un triangolo pari. Se vuoi trovare l`area di un triangolo regolare puoi usare questa formula: area = 1/2 x base x altezza.
- Se hai un triangolo con base 10 e altezza 8, allora l`area = 1/2 x 8 x 10 = 40.

2. Calcola l`area di un quadrato. Per trovare l`area di un quadrato basta moltiplicare uno dei suoi lati per se stesso, perché base e altezza sono uguali per un quadrato.

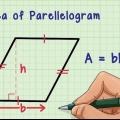
3. Calcola l`area di un rettangolo. Per trovare l`area di un rettangolo tutto ciò che devi fare è moltiplicare la sua base per la sua altezza.

4.Calcola l`area di un trapezio. Per trovare l`area di un trapezio, puoi usare la seguente formula: area = [(base 1 + base 2) x altezza]/2.
Parte 3 di 3: Trovare l`area di un poligono irregolare

1. Utilizzare le coordinate dei nodi per calcolare l`area. Se conosci le coordinate puoi calcolare l`area di un poligono irregolare.

2. Crea una sequenza. Elenca le coordinate xey di ciascun vertice del poligono, in senso antiorario. Ripetere le coordinate del primo punto in fondo all`elenco.

3. Moltiplica la coordinata x di ciascun vertice per la coordinata y del vertice successivo. Somma i risultati. La somma di questi prodotti è 82.

4. Moltiplica la coordinata y di ciascun vertice per la coordinata x del vertice successivo. Somma i risultati. La somma di questi prodotti è -38.

5. Sottrarre la somma dei prodotti calcolati al punto 4 dalla somma dei prodotti calcolati al punto 3. (82) - (-38) = 120.

6. Dividi questo risultato per 2 per trovare l`area del poligono. Area = 120/2 = 60.
Consigli
- Se si elencano i punti in senso orario invece che antiorario si ottiene anche l`area, ma negativa. Ad esempio, puoi usarlo come strumento per determinare la sequenza ciclica di un insieme di punti che formano un poligono.
- Questa formula calcola l`area con l`orientamento. Se lo usi su una forma in cui due delle linee si intersecano come in un 8, ottieni l`area in senso antiorario meno l`area in senso orario.
Articoli sull'argomento "Calcola l'area di un poligono"
Condividi sui social network:
Popolare