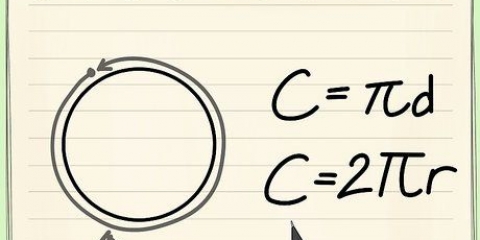Calcolo della Circonferenza per Area: 10 Passaggi (con Immagini)

Contenuto

Passi
- Metodo 1 di 2: Utilizzo dell`equazione del perimetro
- Metodo 2 di 2: risolvere il problema al contrario

La formula per calcolare la circonferenza (C) di un cerchio, C = πD o C = 2πR, è semplice se si conosce il diametro (D) o il raggio (R) del cerchio. Ma cosa fai se conosci solo l`area del cerchio? Come molte cose in matematica, ci sono molteplici soluzioni a questo problema. La formula C = 2√πA serve per trovare la circonferenza di un cerchio utilizzando l`area (A). Puoi anche invertire l`equazione A = πR per trovare R, quindi inserire R nell`equazione del perimetro. Entrambe le equazioni danno lo stesso risultato.

Passi

Metodo 1 di 2: Utilizzo dell`equazione del perimetro

Immagine titolata Trova la circonferenza di un cerchio usando la sua area Passaggio 1

1. Usa la formula C=2√πA per risolvere il problema. Questa formula calcola la circonferenza di un cerchio se conosci solo la sua area. C sta per il perimetro e A per l`area. Scrivi questa formula per iniziare a risolvere il problema.

Il simbolo π, che sta per pi, è un decimale ripetuto con (ormai) migliaia di cifre dopo il punto decimale. Per semplicità, usa 3.14 come valore di pi.
Dal momento che devi comunque convertire pi nella sua forma numerica, usa 3.14 nell`equazione dall`inizio. Scrivilo come C = 2√3,14 x A.

Immagine titolata Trova la circonferenza di un cerchio usando la sua area Passaggio 2

2. Includere l`area come A nell`equazione. Poiché conosci già l`area del cerchio, questo è il valore di A. Quindi procedere alla risoluzione del problema utilizzando l`ordine delle operazioni.

Diciamo che l`area del cerchio è 500 cm. Quindi risolvi l`equazione come segue: 2√3,14 x 500.

Immagine titolata Trova la circonferenza di un cerchio usando la sua area Passaggio 3

3. Moltiplica pi greco per l`area del cerchio. Nell`ordine delle operazioni, le operazioni all`interno del simbolo della radice quadrata vengono per prime. Moltiplica pi per l`area del cerchio che hai collegato. Quindi collega quel risultato all`equazione.

Se il calcolo è uguale a 2√3,14 x 500, allora calcoli prima 3,14 x 500 = 1570. Quindi calcola 2√1.570.

Immagine titolata Trova la circonferenza di un cerchio usando la sua area Passaggio 4

4. Particolareradice quadrata della somma. Esistono diversi modi per calcolare la radice quadrata. Se stai usando una calcolatrice, premi la funzione √ e digita il numero. Puoi anche risolvere il problema manualmente usando i fattori primi.

La radice quadrata di 1570 è 39,6.

Immagine titolata Trova la circonferenza di un cerchio usando la sua area Passaggio 5

5. Moltiplica la radice quadrata per 2 per trovare il perimetro. Infine, completi il calcolo moltiplicando il risultato per 2. Questo restituisce un numero finale, la circonferenza.

Calcola 39,6 x 2 = 79,2. Ciò significa che la circonferenza è 79,2 cm, il che risolve la formula.

Metodo 2 di 2: risolvere il problema al contrario

Immagine titolata Trova la circonferenza di un cerchio usando la sua area Passaggio 6

1. Usa la formula A = πR in. Questa è la formula per l`area di un cerchio. A sta per l`area e R per il raggio. Normalmente lo useresti se conoscessi il raggio, ma puoi anche riempire l`area per risolvere l`equazione.

Ancora una volta, usa 3.14 come valore arrotondato per pi.

Immagine titolata Trova la circonferenza di un cerchio usando la sua area Passaggio 7

2. Immettere l`area come valore per A. Usa l`area del cerchio nell`equazione. Mettilo a sinistra dell`equazione come valore per A.

Supponiamo che l`area del cerchio sia 200 cm. L`equazione diventa quindi 200 = 3,14 x R.

Immagine titolata Trova la circonferenza di un cerchio usando la sua area Passaggio 8

3. Dividi entrambi i membri dell`equazione per 3,14. Per risolvere questo tipo di equazione, devi eliminare gradualmente i passaggi a destra eseguendo le operazioni opposte. Poiché conosci il valore di pi, dividi ciascun lato per quel valore. Questo elimina pi a destra e ti dà un nuovo valore numerico a sinistra.

Se dividi 200 per 3,14, il risultato è 63,7. Quindi la nuova equazione è 63,7 = R.

Immagine titolata Trova la circonferenza di un cerchio usando la sua area Passaggio 9

4. Particolareradice quadrata del risultato per ottenere il raggio del cerchio. Quindi l`esponente a destra dell`equazione viene eliminato. L`opposto di "esponenziale" è trovare la radice quadrata del numero. Trova la radice quadrata di ciascun lato dell`equazione. Questo rimuove l`esponente a destra e mette il raggio a sinistra.

La radice quadrata di 63,7 è 7,9. L`equazione diventa quindi 7,9 = R, il che significa che il raggio del cerchio è 7,9. Questo ti darà tutte le informazioni necessarie per trovare il perimetro.

Immagine titolata Trova la circonferenza di un cerchio usando la sua area Passaggio 10

5.Determina la circonferenza del cerchio usando il raggio. Ci sono due formule per trovare il perimetro (C). Il primo è C = πD, dove D è il diametro. Moltiplica il raggio per 2 per trovare il diametro. Il secondo è C = 2πR. Moltiplica 3,14 per 2 e poi moltiplica il risultato per il raggio. Entrambe le formule ti daranno lo stesso risultato.

Usa la prima opzione, 7,9 x 2 = 15,8, il diametro del cerchio. Questo diametro moltiplicato per 3,14 è 49,6.

Per la seconda opzione, il calcolo diventa 2 x 3,14 x 7,9. Per prima cosa calcoli 2 x 3,14 = 6,28 e quello moltiplicato per 7,9 è 49,6. Nota come entrambi i metodi ti danno la stessa risposta.