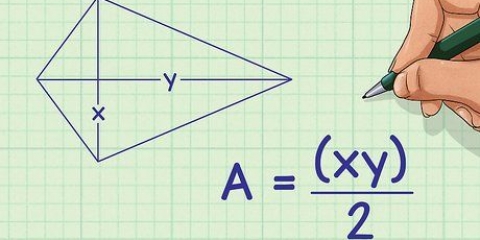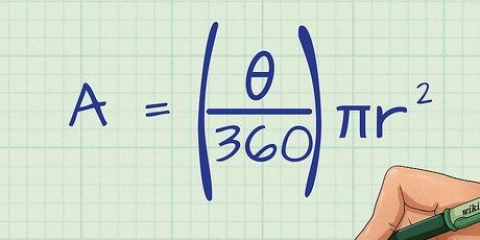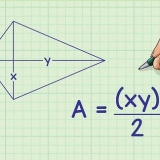Nel nostro esempio, l`area del triangolo=½ x 3 x 2=3. 
Nel nostro esempio, A(totale del pentagono)=5 x A(triangolo)=5 x 3=15. 



Il base del triangolo è ½ volte il lato del pentagono. Nel nostro esempio questo è ½ x 7=3,5 unità. Il angolo al centro del pentagono è sempre 36º. (Supponendo 360º per un cerchio completo, puoi dividerlo in 10 triangoli più piccoli. 360 ÷ 10=36, quindi l`angolo di un tale triangolo è 36º). 
In un triangolo rettangolo, l`è tangente di un angolo uguale alla lunghezza del lato opposto, divisa per la lunghezza del lato adiacente. Il lato opposto all`angolo di 36º è la base del triangolo (metà del lato del pentagono). Il lato adiacente dell`angolo di 36º è l`altezza del triangolo. tan(36º)=opposto / adiacente Nel nostro esempio, tan(36º)=3,5 / altezza altezza x abbronzatura(36º)=3,5 altezza=3,5 / abbronzatura (36º) altezza=(circa) 4.8. 
Nel nostro esempio, l`area di uno dei triangoli piccoli è=½bh=½(3.5)(4.8)=8.4. 
Nel nostro esempio, l`area dell`intero pentagono=8,4 x 10=84. 

Area di un pentagono regolare=(5S ) / (4tan(36º)), dove S=lunghezza di un lato. abbronzatura(36º)=√(5-2√5). Se la tua calcolatrice non ha una funzione `abbronzatura`, usa la formula per l`area: Area=(5S) / (4√(5-2√5)). 
L`area di un pentagono regolare=(5/2)Rsin(72º), dove R il raggio è.
Calcola l'area di un pentagono
Contenuto
Un pentagono è un poligono con cinque lati diritti. Quasi tutti i problemi che incontrerai durante le lezioni di matematica riguarderanno pentagoni regolari, con cinque lati uguali. Ci sono due modi comuni per calcolare l`area, a seconda di quante informazioni hai.
Passi
Metodo 1 di 3: Determinazione dell`area utilizzando i lati e l`apotema

1. Inizia con la lunghezza del lato e l`apotema. Questo metodo funziona per pentagoni regolari, con cinque lati uguali. Oltre alla lunghezza del lato ci vuole l`apotema del pentagono. L`apotema è la linea dal centro del pentagono a un lato, che interseca il lato perpendicolarmente (cioè con un angolo di 90º).
- Non confondere l`apotema con il raggio di un poligono, perché interseca un angolo (vertice) anziché un punto al centro del lato. Se conosci solo la lunghezza di un lato e il raggio, passa al metodo successivo.
- Come esempio usiamo un pentagono con lato 3 e apotema 2.

2. Dividi il pentagono in cinque triangoli. Disegna cinque linee dal centro del pentagono, ciascuna che porta a un vertice (angolo). Ora hai cinque triangoli.

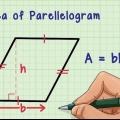
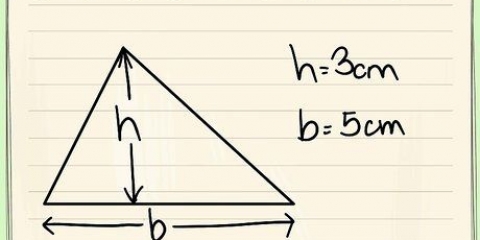
3. Calcola l`area di un triangolo. Ogni triangolo ha a base uguale al lato del pentagono. Ha anche un altezza che è uguale all`apotema. (Ricorda, l`altezza di un triangolo è la lunghezza del lato che è perpendicolare alla sua base e si estende fino a un vertice). Per calcolare l`area di un triangolo si usa ½ x base x altezza.

4. Moltiplica per cinque per l`area totale del pentagono. Abbiamo diviso il pentagono in cinque triangoli uguali. Per calcolare l`area totale, moltiplica per cinque l`area di un triangolo.
Metodo 2 di 3: Determinazione dell`area utilizzando la lunghezza di un lato

1. Inizia con la lunghezza di un lato. Questo metodo funziona solo per pentagoni regolari, che hanno cinque lati di uguale lunghezza.
- In questo esempio utilizziamo un pentagono con lunghezza 7 per ogni lato.

2. Dividi il pentagono in cinque triangoli. Disegna una linea dal centro del pentagono a un vertice. Ripetere per ogni vertice. Ora hai cinque triangoli, ciascuno della stessa dimensione.

3. Dividi un triangolo a metà. Disegna una linea dal centro del pentagono alla base di un triangolo. Questa linea dovrebbe intersecare la base ad angolo retto (90º), che divide il triangolo in due triangoli uguali e più piccoli.

4. Etichetta uno dei triangoli più piccoli. Possiamo già etichettare un lato e un angolo del triangolo più piccolo:

5. Calcola l`altezza del triangolo. Il altezza di questo triangolo è il lato perpendicolare al lato del pentagono che porta al centro. Usiamo una semplice trigonometria per determinare la lunghezza di questo lato:

6.Calcola l`area del triangolo. L`area di un triangolo è uguale a ½ base x altezza. (LA=½bh.) Ora che conosci l`altezza, inserisci questi valori per determinare l`altezza del tuo piccolo triangolo.

7. Moltiplica per trovare l`area del pentagono. Uno di questi triangoli più piccoli copre 1/10 dell`area del pentagono. Per l`area totale, moltiplica per 10 l`area del triangolo più piccolo.
Metodo 3 di 3: Utilizzo di una formula

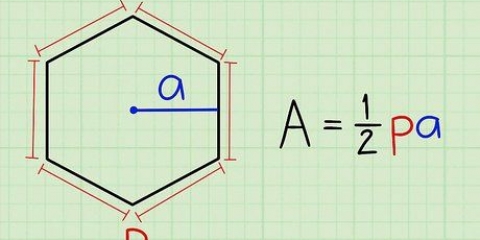
1. Usa il contorno e l`apotema. L`apotema è una linea dal centro di un pentagono che interseca un lato ad angolo retto. Se viene data la lunghezza, puoi utilizzare questa semplice formula.
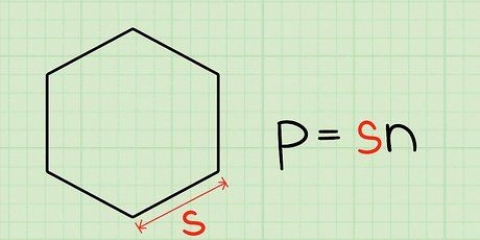
- Area di un pentagono regolare=papà / 2, dove P=la circonferenza e un=l`apotema.
- Se non conosci la circonferenza calcolala utilizzando la lunghezza del lato: p=5s, dove s è la lunghezza del lato.

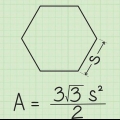
2. Usa la lunghezza del lato. Se conosci solo la lunghezza dei lati, usa la seguente formula:

3. Scegli una formula che utilizzi solo il raggio. Puoi persino trovare l`area se conosci solo il raggio. Usa la seguente formula:
Consigli
- I pentagoni irregolari o i pentagoni con lati disuguali sono più difficili da studiare. L`approccio migliore è di solito dividere il pentagono in triangoli e sommare le aree di tutti i triangoli. Potrebbe anche essere necessario disegnare una forma più grande attorno al pentagono, calcolarne l`area e quindi sottrarre l`area dello spazio extra.
- Se possibile, usa sia un metodo geometrico che una formula e confronta i risultati per verificare la tua risposta. Le risposte possono differire leggermente se si compila la formula completamente in una volta (perché mancano i passaggi in cui si completa), ma dovrebbero essere molto vicini l`uno all`altro.
- Gli esempi forniti qui utilizzano valori arrotondati per semplificare i calcoli. Se hai un vero poligono con le lunghezze dei lati specificate, otterrai risultati leggermente diversi per le altre lunghezze e aree.
- Le formule sono derivate da metodi geometrici, simili a quelli qui descritti. Cerca di capire come distrarli tu stesso. La formula del raggio è più difficile da ricavare rispetto alle altre (suggerimento: è necessaria l`identità del doppio angolo).
Articoli sull'argomento "Calcola l'area di un pentagono"
Condividi sui social network:
Popolare