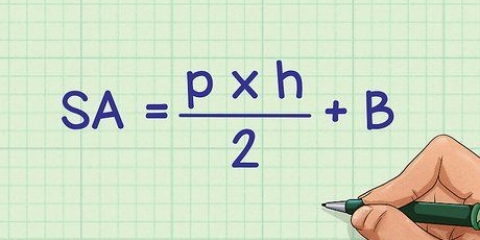Come Calcolare l'Area di un Quadrilatero

Contenuto

Passi

Quindi per i tuoi compiti devi calcolare l`area di un quadrilatero...ma non hai nemmeno la più pallida idea di cosa sia un quadrilatero. Niente panico: il salvataggio è vicino! Un quadrilatero è qualsiasi figura composta da 4 lati/angoli. Tutto quello che devi fare è determinare il tipo quadrilatero del problema e utilizzare la formula corrispondente per calcolare l`area.

Passi

Metodo 1 di 4: quadrati, rettangoli e altri parallelogrammi

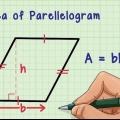
1. Scopri come determinare cos`è un parallelogramma. Un parallelogramma è qualsiasi quadrilatero con 2 coppie di lati paralleli, dove i lati paralleli sono di uguale lunghezza. Quadrati, rettangoli e rombi sono tutti parallelogrammi.

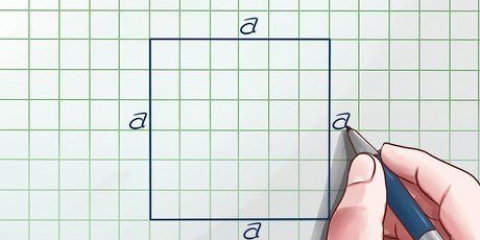
2. Trova l`area di un quadrato. Poiché ogni lato di un quadrato ha la stessa lunghezza, tutto ciò che devi fare è misurare la lunghezza di 1 lato (chiamalo "T"), per trovare l`area di un quadrato. Questo equivale a moltiplicare la base del quadrato per la sua altezza; la base e l`altezza sono sempre le stesse. Usa la seguente formula:

K = t

Questo è lo stesso di K = t * t

Se un lato di un quadrato ha una lunghezza di 4, (t = 4), allora l`area è t, o 4 x 4 = 16.

3. Trova l`area di un rettangolo. Per trovare l`area di un rettangolo è necessario conoscere la lunghezza e la larghezza del rettangolo. La formula è la seguente:

K = b*h

Se la lunghezza è 10 e la larghezza è 5, l`area del rettangolo è 10 x 5 (l * w) = 50.

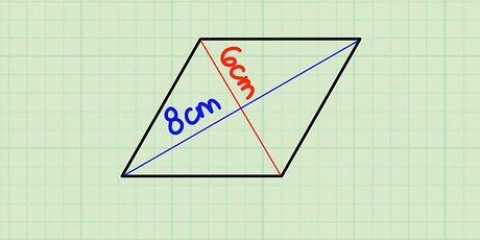
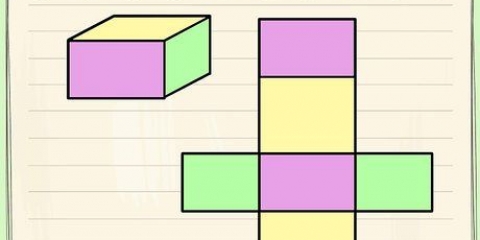
4. Trova l`area di un quadrato. Questo può essere complicato: non puoi semplicemente moltiplicare un lato per l`altro qui. Ora dovrai disegnare linee da ogni punto e misurare le diagonali della forma, se non date. Quindi moltiplica le diagonali in questo modo:

K = (b*h)/2, per cui b = diagonale 1 e h = diagonale 2

Se un quadrato ha diagonali di lunghezza 6 allora 8, allora l`area è (6 x 8)/2 = 48/2 = 24

Metodo 2 di 4: L`area di un trapezio

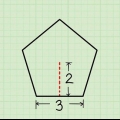
1. Determina se si tratta di un trapezio. Un trapezio è un quadrilatero con almeno 2 lati paralleli. Ciascuno dei quattro lati di un trapezio può avere una lunghezza diversa. Esistono due modi diversi per trovare l`area di un trapezio, a seconda delle informazioni fornite.

2. Determina l`altezza del trapezio. L`altezza di un trapezio è la linea perpendicolare che collega la linea di base superiore e la linea di base inferiore e sono necessarie entrambe per calcolare l`area. Questo è non della stessa lunghezza di uno dei lati, perché ogni lato è diagonale. Ecco come trovare l`altezza:

Determina qual è la base più breve. Posiziona la matita nell`angolo tra la linea di base e traccia una linea verso l`alto o verso il basso fino all`altra linea di base. Ora dovresti aver disegnato un triangolo con un angolo di 90 gradi.

Usa la trigonometria per determinare l`altezza. Ad esempio, se conosci la lunghezza di un lato e l`angolo adiacente è noto e c`è un angolo di 90 gradi nel triangolo, l`altezza è la lunghezza del lato moltiplicata per il seno dell`angolo.

Supponiamo che l`altezza del trapezio sia 10.

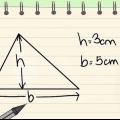
3. Determina l`area del trapezio usando l`altezza e la lunghezza della base. Se conosci l`altezza del trapezio e la lunghezza di entrambi i lati della base, usa la seguente formula:

K = (a+b)/2 * h

Se l`altezza è 10 e la base ha una lunghezza di 7 e 9, puoi trovare l`area calcolando: (7 + 9)/2 * 10 = (16/2) * 10 = 8 * 10 = 80

4. Trova l`area di un trapezio usando il segmento medio. Questo segmento medio è una linea che corre parallela alle linee inferiore e superiore del trapezio e ha una lunghezza esattamente nel mezzo. Ecco come lavori:

Determina il segmento centrale. Per determinare la lunghezza del segmento medio m, prendiamo la media delle lunghezze dei lati un e B (o la linea inferiore e superiore del trapezio).Usa la formula: m = (a+b)/2.Ora che conosci la lunghezza del segmento centrale, puoi moltiplicarla per l`altezza per trovare l`area. Usa la seguente formula:

K = m*h

Questa è essenzialmente la stessa formula dell`originale, ma ora la sostituisce "m" il termine (a + b)/2.

Supponiamo di conoscere il segmento centrale di questo trapezio. Supponiamo che questo sia 8, quindi l`area del trapezio sia 8 x 10 = 80, proprio come con il metodo precedente.

Metodo 3 di 4: Determinazione della superficie di un aquilone

1. Cos`è un aquilone. Un aquilone è definito come una forma geometrica in cui 2 paia di lati di uguale lunghezza sono collegati tra loro, che assomiglia a un normale aquilone. Esistono due modi diversi per trovare l`area di questa figura, a seconda delle informazioni fornite.

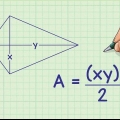
2. Trova l`area di un aquilone usando la lunghezza dei suoi lati. Se conosci la lunghezza di due lati diversi di un aquilone e conosci l`angolo tra quei lati, usa la seguente formula in cui l`angolo è uguale a theta (θ):

K =(a*b) * peccato θ

3. Trova l`area di un aquilone usando le diagonali. Una diagonale è la linea retta tra due angoli opposti dell`aquilone. Ogni aquilone ha 2 diagonali.

Determina la lunghezza di ciascuna diagonale. Disegna una linea da un angolo di un aquilone a quello opposto. Ora dovresti avere 2 triangoli. Determina l`utilizzo Questo articolo, qual è la lunghezza della diagonale (i tre angoli di un triangolo sommano fino a 180 gradi).

Una volta determinata la prima diagonale, utilizzare gli stessi principi per determinare la lunghezza dell`altra. Quindi utilizzare questa formula per determinare l`area, dove P e Q rappresentare la lunghezza delle diagonali:

K = (p*q)/2

Se le diagonali hanno lunghezze 4 e 6, allora puoi trovare l`area dell`aquilone come segue: (4 x 6)/2 = 24/2 = 12

Nota che questa formula funziona anche per l`area di un rombo, poiché si tratta di un tipo speciale di aquilone, in cui tutti i lati hanno la stessa lunghezza.

Metodo 4 di 4: una formula generale

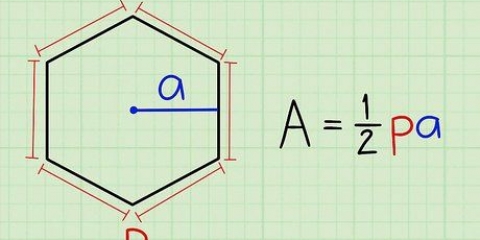
1. La formula generale per determinare l`area di un quadrilatero. Esistono formule per determinare l`area di qualsiasi quadrilatero, indipendentemente dalla sua forma. Ecco la forma più generale, utilizzando i principi trigonometrici:

Se K è l`area totale del quadrilatero, un, B, C e D rappresentano le lunghezze dei 4 lati, un è l`angolo (in gradi) tra i lati un e D e C è l`angolo (in gradi) tra i lati B e C, poi:
K = 0.5*a*d * sin A + 0.5*b*c * peccato C
Se stai cercando di trovare l`area di un parallelogramma in cui gli angoli opposti sono uguali, la formula diventa più semplice: K = 0.5*(ad + bc) * sin A.