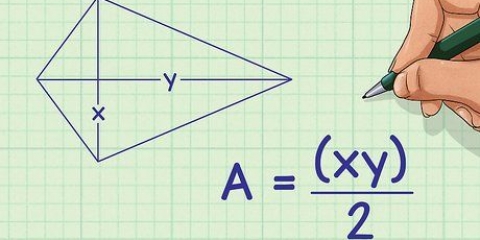Istruzioni passo passo gratis 
Area = 1/2 x (3 cm x 5 cm) 
Area = 1/2 x (3 cm x 5 cm) Superficie = 1/2 x 15 cm Area = 7.5 cm 
Area = √{6 (6 - 3)(6 - 4)(6 - 5)} 
6 - 3 = 3 6 - 4 = 2 6 - 5 = 1 Area = √{6 (3)(2)(1)} 
Area = 1/2(b)(c) x sin A Area = 1/2(150)(231) x sin A 
Area = 1/2(150)(231) x sin A Area = 1/2(34.650) x sin A Area = 17.325 x sin A Area = 17.325 x .8386705 Superficie = 14.530 cm
Calcola l'area di un triangolo
Contenuto
Sebbene il metodo più comune per calcolare l`area di un triangolo sia moltiplicare la sua metà base per la sua altezza, esistono numerosi altri modi per calcolare l`area di un triangolo, a seconda dei dati disponibili. Ciò include la lunghezza di tutti e tre i lati, la lunghezza di un lato di un triangolo equilatero e la lunghezza di due lati insieme all`angolo incluso. Leggi qui come puoi calcolare l`area di un triangolo usando questi dati.
Passi
Metodo 1 di 4: con la base e l`altezza
1. Determina la base e l`altezza del tuo triangolo. La base del triangolo è la lunghezza di un lato, che di solito è il lato inferiore del triangolo. L`altezza è la lunghezza dalla base all`angolo superiore del triangolo, che è perpendicolare alla base. In un triangolo rettangolo, la base e l`altezza sono i due lati che si incontrano ad un angolo di 90 gradi. Ma, in un altro triangolo, come si vede sotto, la linea dell`altitudine taglierà proprio attraverso la forma.
- Dopo aver determinato la base e l`altezza del triangolo, sei pronto per iniziare a utilizzare la formula.
2. Scrivi la formula per trovare l`area di un triangolo. La formula per questo tipo di problema è Area = 1/2 (base x altezza), o 1/2 (reggiseno). Dopo aver annotato tutto, puoi iniziare a riempire la lunghezza dell`altezza e la base.
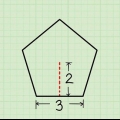
3. Immettere i valori di base e altezza. Trova la base e l`altezza del triangolo e usa questi valori nell`equazione. In questo esempio, l`altezza del triangolo è 3 cm e la base del triangolo è 5 cm. Ecco come apparirà la formula dopo aver inserito questi valori:
4. Risolvi l`equazione. Puoi moltiplicare prima l`altezza per la base perché quei valori sono tra parentesi. Quindi moltiplichi il risultato per 1/2. Ricorda che darai la risposta in metri quadrati perché stai lavorando in uno spazio bidimensionale. Ecco come risolvere questo problema per la risposta finale:
Metodo 2 di 4: utilizzo della lunghezza di ciascun lato (formula di Heron)
1. Calcola il semiperimetro (semiperimetro) del triangolo. Per trovare il mezzo perimetro del triangolo non devi fare altro che sommare tutti i lati e dividere il risultato per due. La formula per trovare il semiperimetro di un triangolo è la seguente: semiperimetro = (lunghezza lato a + lunghezza lato b + lunghezza lato c) / 2, o s = (a + b + c) / 2. Poiché sono date tutte e tre le lunghezze del triangolo rettangolo, 3 cm, 4 cm e 5 cm, puoi inserirle direttamente nelle formule e risolvere il problema per il semi perimetro:
- s = (3 + 4 + 5)/2
- s = 12/2
- s = 6
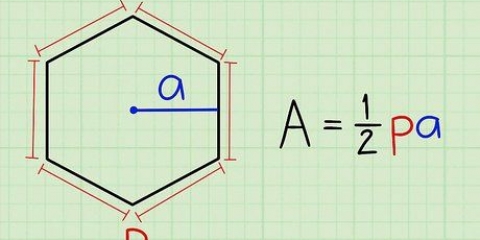
2. Inserisci i valori corretti nella formula per trovare l`area di un triangolo. Questa formula per trovare l`area di un triangolo è anche chiamata formula di Heron e funziona così: Area = √{s (s - a)(s - b)(s - c)}. Ripetiamo il passaggio precedente dove S la mezza circonferenza è e un, B, e C i tre lati del triangolo. Utilizza la seguente sequenza di operazioni: inizia risolvendo tutto tra parentesi, poi tutto sotto il segno radicale e infine la radice quadrata stessa. Ecco come apparirà questa formula dopo aver inserito tutti i valori noti:
3. Sottrarre i valori tra parentesi. Quindi: 6 - 3, 6 - 4 e 6 - 5. Ecco il risultato sulla carta:
4. Moltiplica i risultati di queste operazioni. Moltiplica 3 x 2 x 1 per ottenere 6 come risposta. Devi moltiplicare questi numeri insieme prima di moltiplicarli per 6 perché sono tra parentesi.
5. Moltiplica il risultato precedente per metà della circonferenza. Quindi moltiplica il risultato, 6, per la mezza circonferenza, che è anche 6. 6 x 6 = 36.
6. Calcola la radice quadrata. 36 è un quadrato perfetto e √36 = 6. Non dimenticare l`unità con cui hai iniziato: centimetri. Esprimi la risposta finale in centimetri quadrati. L`area del triangolo con i lati 3, 4 e 5 è di 6 cm.
Metodo 3 di 4: utilizzo di un lato di un triangolo rettangolare
1. Trova il lato del triangolo equilatero. Un triangolo equilatero ha i lati di uguale lunghezza e angoli uguali. Sai che hai a che fare con un triangolo equilatero, o perché è un dato di fatto, o perché sai che tutti gli angoli e tutti i lati hanno lo stesso valore. Il valore di uno dei lati di questo triangolo è 6 cm. Nota questo.
- Se sai di avere a che fare con un triangolo equilatero ma solo il perimetro è noto, dividi semplicemente questo valore per 3. Ad esempio, la lunghezza di un lato di un triangolo equilatero con perimetro 9 è molto semplicemente 9/3, o 3.
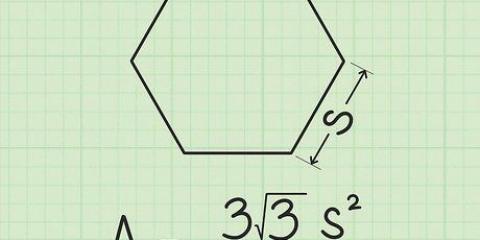
2. Annota la formula per trovare l`area di un triangolo equilatero. La formula per questo tipo di problema è area = (s^2)(√3)/4. Notare che S "seta" significa.
3. Applicare il valore di un lato all`equazione. Per prima cosa calcola il quadrato del lato con valore 6, per ottenere 36. Quindi trova il valore di √3, se la risposta deve essere data in decimali. Ora inserisci √3 nella calcolatrice per ottenere 1.732 per ottenere. Dividi questo numero per 4. Nota che puoi anche dividere 36 per 4 e poi moltiplicare per √3 -- l`ordine delle operazioni non ha effetto sulla risposta.
4. Risolvere. Ora si tratta principalmente di contare. 36 x √3/4 = 36 x .433 = 15.59 cm L`area di un triangolo equilatero con un lato lungo 6 cm è 15.59 cm.
Metodo 4 di 4: utilizzo della lunghezza di due lati e dell`angolo incluso
1. Trova il valore delle lunghezze di due lati e l`angolo incluso. L`angolo incluso è l`angolo tra i due lati noti del triangolo. Devi conoscere questi valori per trovare l`area di un triangolo usando questo metodo. Assumiamo un triangolo con le seguenti dimensioni:
- angolo A = 123º
- lato b = 150 cm
- lato c = 231 cm
2. Annota la formula per trovare l`area del triangolo. La formula per trovare l`area di un triangolo con due lati noti e un angolo incluso noto è la seguente: Area = 1/2(b)(c) x sin A. In questa equazione rappresentare "B" e "C" le lunghezze dei lati e "un" l`angolo. Dovresti sempre prendere il seno dell`angolo in questa equazione.
3. Compila i valori nell`equazione. Ecco come appare l`equazione dopo aver inserito questi valori:
4. Risolvere. Per risolvere questa equazione, moltiplica prima i lati e dividi il risultato per due. Quindi moltiplica questo risultato per il seno dell`angolo. Il valore del seno può essere trovato con la calcolatrice. Non dimenticare di dare la tua risposta in unità cubiche. Ecco come farlo:
Consigli
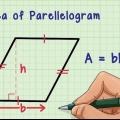
- Se non capisci perché la formula base - altezza funziona in questo modo, ecco una breve spiegazione. Se crei un secondo triangolo identico e lo metti uno accanto all`altro, formerà un rettangolo (due triangoli rettangoli) o un parallelogramma (due triangoli non rettangoli). Per trovare l`area di un rettangolo o di un parallelogramma basta moltiplicare la base per l`altezza. Poiché un triangolo è uguale a metà rettangolo o parallelogramma, ne consegue che l`area di un triangolo è uguale a metà base per la sua altezza.
Articoli sull'argomento "Calcola l'area di un triangolo"
Condividi sui social network:
Popolare
