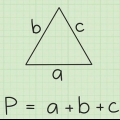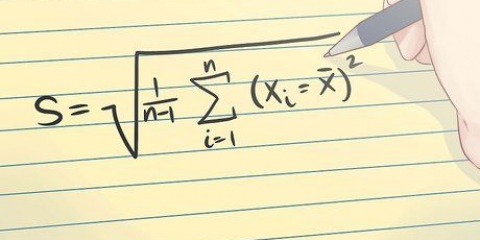Qualsiasi lato del triangolo può essere la base, indipendentemente da come viene disegnato il triangolo. Per immaginarlo, ruota il triangolo nella tua mente finché il lato troppo familiare non è diventato il fondo. Ad esempio, se sai che l`area di un triangolo è 20 e uno dei suoi lati è 4, allora: A = 20 e b = 4. 
Nell`esempio: 20 = 1/2(4)h 20 = 2 ore 10 = h 

Quindi nell`esempio:c =8 e a = 4. 
4 + b = 8 16 + b = 64 b = 48 
b = Sqrt (48) = 6.93
Calcolo dell'altezza di un triangolo
Contenuto
Per calcolare l`area di un triangolo è necessaria la sua altezza. Se queste informazioni non vengono fornite, puoi facilmente calcolarle in base a ciò che sai! Questo articolo ti insegnerà due modi diversi per trovare l`altezza di un triangolo, a seconda delle informazioni che ti sono state fornite.
Passi
Metodo 1 di 2: Determinazione dell`altezza quando l`area e la base sono note

1. La formula per l`area di un triangolo. Questo èLA=1/2bh.
- un = Area del triangolo
- B = Lunghezza della base del triangolo
- h = Altezza della base del triangolo

2. Osserva il triangolo e determina quali variabili sono note. In questo caso conosci già la zona, quindi un è uguale a quel valore.Dovresti anche conoscere il valore di uno dei lati; indicare quel valore "`B`".Se non conosci entrambi i valori o uno di essi, hai bisogno di un altro metodo.

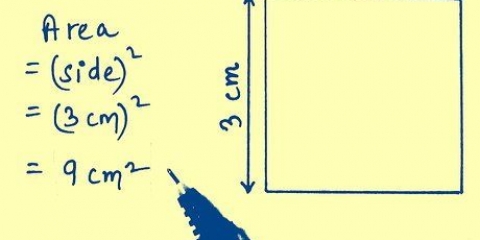
3. Usa i tuoi valori nell`equazioneLA=1/2bh e calcola. Moltiplicare prima la base (b) per 1/2, quindi dividere l`area (A) per il prodotto.Il valore risultante è l`altezza del tuo triangolo!
Metodo 2 di 2: Trovare l`altezza di un triangolo equilatero

1. Le proprietà di un triangolo equilatero. Un triangolo equilatero ha tre lati uguali e tre angoli uguali di 60 gradi ciascuno. Se dividi a metà un triangolo equilatero, otterrai due triangoli rettangoli congruenti.
- In questo esempio useremo un triangolo equilatero con i lati che hanno una lunghezza di 8.
2. Il teorema di Pitagora. Il teorema di Pitagora afferma che per un triangolo rettangolo con i lati di lunghezza un e B, e un`ipotenusa di lunghezza C: a + b = c.Possiamo usare questo teorema per trovare l`altezza del nostro triangolo equilatero!

3. Dividi a metà il triangolo equilatero e assegna valori alle variabiliun, B eC.Lato un è uguale alla metà della lunghezza di un lato, e lato B è l`altezza del triangolo che vogliamo risolvere.

4. Completa i valori del teorema di Pitagora e risolvi b. Per prima cosa calcola il quadrato di C e un moltiplicandolo per se stesso. Quindi sottrarre a da c.

5. Trova la radice quadrata di b per trovare l`altezza del triangolo! Usa la radice quadrata sulla calcolatrice per trovare Sqrt(. La risposta è l`altezza del tuo triangolo equilatero!
Articoli sull'argomento "Calcolo dell'altezza di un triangolo"
Condividi sui social network:
Popolare