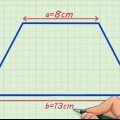
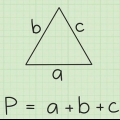Ad esempio, se hai un trapezio con una parte superiore di 2 cm, una parte inferiore di 3 cm e due lunghezze laterali di 1 cm, la tua formula sarebbe simile a questa:


Ad esempio:


La circonferenza del trapezio è quindi di 7 cm. 

Ad esempio, se hai un trapezio con un`altezza di 6 cm, devi tracciare una linea da ciascun vertice superiore verso il basso. Nota 6 cm per riga. 
Ad esempio, se la parte superiore del trapezio misura 6 cm, anche la parte centrale del fondo misura 6 cm. 

Ad esempio, se sai che l`altezza del trapezio è 6 cm e la lunghezza del lato (ipotenusa) è 9 cm, la tua equazione sarebbe simile a questa:


Ad esempio: è l`equazione  , poi fai il quadrato 6 e 9 e sottrai il quadrato di 6 dal quadrato di 9:
, poi fai il quadrato 6 e 9 e sottrai il quadrato di 6 dal quadrato di 9:




Ad esempio:




Quindi prendi nota come base del primo triangolo.
come base del primo triangolo. 
Ad esempio, se il secondo lato del trapezio è 7 cm, calcola come segue:





Quindi prendi nota come base del secondo triangolo.
come base del secondo triangolo. 
Ad esempio: 
Dopo aver convertito le radici quadrate in decimali, hai
Quindi, la circonferenza approssimativa del tuo trapezio è 38,314 cm.. 

Ad esempio, se hai un trapezio con un`altezza di 6 cm, traccia una linea da ciascun vertice superiore verso il basso. Nota 6 cm ad ogni riga. 
Ad esempio, se la parte superiore del trapezio misura 6 cm, anche la parte centrale del fondo misura 6 cm. 
Con questo rapporto puoi trovare la lunghezza dell`ipotenusa del triangolo, che è anche il primo lato del trapezio. L`ipotenusa è il lato opposto all`angolo di 90 gradi di un triangolo rettangolo. 
Supponiamo che l`angolo interno dato sia 35 gradi e l`altezza del triangolo sia 6 cm, quindi la tua formula sarà simile a questa:


Ad esempio, utilizzando una calcolatrice scoprirai che il seno di un angolo di 35 gradi è 0,5738 (arrotondato). Quindi la tua formula ora è:


Ad esempio:




Pertanto, la lunghezza dell`ipotenusa e del primo lato mancante del trapezio è di circa 10,4566 cm. 
Ad esempio, se l`angolo interno specificato è di 45 gradi, calcola:





Quindi la lunghezza dell`ipotenusa e del secondo lato mancante del trapezio è di circa 8,4854 cm. 

Ad esempio, se il primo triangolo rettangolo ha un`ipotenusa di 10,4566 e un`altezza di 6, la tua formula è:


Ad esempio:






Quindi la base del triangolo e la prima parte mancante del fondo del trapezio è di circa 8,5639 cm. 
Ad esempio, se il secondo triangolo rettangolo ha un`ipotenusa di 8,4854 e un`altezza di 6, dovresti calcolare come segue:






Quindi la base del secondo triangolo, e la seconda parte mancante del fondo del trapezio, è pari a 6 cm. 
Ad esempio: 
Quindi la circonferenza approssimativa del trapezio è 45,5059 cm.
Calcolo del perimetro di un trapezio
Contenuto
Un trapezio è definito come un quadrilatero con due lati paralleli. Come con qualsiasi poligono, è necessario sommare tutti e quattro i lati per trovare il perimetro di un trapezio (o trapezio). Spesso, tuttavia, ti mancheranno le lunghezze laterali, ma hai altri dati, come l`altezza del trapezio o le misurazioni dell`angolo. Usando questi dati, puoi trovare le lunghezze sconosciute dei lati usando le regole della geometria e della trigonometria.
Passi
Metodo 1 di 3: se conosci la lunghezza di entrambi i lati e la base

1. Imposta la formula per la circonferenza di un trapezio. La formula è  , per cui
, per cui  è uguale al perimetro del trapezio e alla variabile
è uguale al perimetro del trapezio e alla variabile  è uguale alla lunghezza della sommità del trapezio,
è uguale alla lunghezza della sommità del trapezio,  è uguale alla lunghezza del fondo,
è uguale alla lunghezza del fondo,  è uguale alla lunghezza del lato sinistro e
è uguale alla lunghezza del lato sinistro e  è uguale alla lunghezza del lato destro.
è uguale alla lunghezza del lato destro.
 , per cui
, per cui  è uguale al perimetro del trapezio e alla variabile
è uguale al perimetro del trapezio e alla variabile  è uguale alla lunghezza della sommità del trapezio,
è uguale alla lunghezza della sommità del trapezio,  è uguale alla lunghezza del fondo,
è uguale alla lunghezza del fondo,  è uguale alla lunghezza del lato sinistro e
è uguale alla lunghezza del lato sinistro e  è uguale alla lunghezza del lato destro.
è uguale alla lunghezza del lato destro.
2. Usa le lunghezze laterali nella formula. Se non conosci la lunghezza di tutti e quattro i lati del trapezio, non puoi usare questa formula.


3. Aggiungi le lunghezze dei lati insieme. Questo ti darà la circonferenza del tuo trapezio.


La circonferenza del trapezio è quindi di 7 cm.
Metodo 2 di 3: se conosci l`altezza, entrambe le lunghezze dei lati e la lunghezza superiore

1. Dividi il trapezio in un rettangolo e due triangoli rettangoli. Per fare ciò, disegna l`altezza da entrambi gli angoli superiori.
- Se non riesci a formare i due triangoli rettangoli perché un lato del trapezio è perpendicolare alla base, assicurati che questo lato abbia la stessa lunghezza dell`altezza e dividi il trapezio in un rettangolo e un triangolo rettangolo.

2. Indica la lunghezza di ciascuna linea di contorno. Poiché questi sono i lati opposti di un rettangolo, avranno la stessa lunghezza.

3. Nota la lunghezza della parte centrale del fondo. (Questa è la parte inferiore del rettangolo.) La lunghezza sarà uguale alla lunghezza della parte superiore (la parte superiore del rettangolo), perché i lati opposti di un rettangolo hanno la stessa lunghezza. Se non conosci la lunghezza della parte superiore, non puoi utilizzare questo metodo.

4. Imposta il teorema di Pitagora per il primo triangolo rettangolo. La formula è  , per cui
, per cui  è la lunghezza dell`ipotenusa del triangolo rettangolo (il lato opposto all`angolo retto),
è la lunghezza dell`ipotenusa del triangolo rettangolo (il lato opposto all`angolo retto),  è l`altezza del triangolo rettangolo e
è l`altezza del triangolo rettangolo e  è la lunghezza della base del triangolo.
è la lunghezza della base del triangolo.
 , per cui
, per cui  è la lunghezza dell`ipotenusa del triangolo rettangolo (il lato opposto all`angolo retto),
è la lunghezza dell`ipotenusa del triangolo rettangolo (il lato opposto all`angolo retto),  è l`altezza del triangolo rettangolo e
è l`altezza del triangolo rettangolo e  è la lunghezza della base del triangolo.
è la lunghezza della base del triangolo.
5. Usa i valori noti del primo triangolo nella formula. Assicurati di inserire la lunghezza laterale del trapezio per  . Immettere l`altezza del trapezio per
. Immettere l`altezza del trapezio per  .
.
 . Immettere l`altezza del trapezio per
. Immettere l`altezza del trapezio per  .
.

6. Al quadrato i valori noti nell`equazione. Quindi sottrai i valori al quadrato l`uno dall`altro per ottenere  isolare.
isolare.
 isolare.
isolare. , poi fai il quadrato 6 e 9 e sottrai il quadrato di 6 dal quadrato di 9:
, poi fai il quadrato 6 e 9 e sottrai il quadrato di 6 dal quadrato di 9:



7. Prendi la radice quadrata per ottenere il valore di B  trovare. (Per istruzioni complete sulla semplificazione delle radici quadrate, leggi questo articolo sull`argomento). Il risultato ti darà il valore della base mancante del tuo primo triangolo rettangolo. Scrivi questa lunghezza alla base del tuo triangolo.
trovare. (Per istruzioni complete sulla semplificazione delle radici quadrate, leggi questo articolo sull`argomento). Il risultato ti darà il valore della base mancante del tuo primo triangolo rettangolo. Scrivi questa lunghezza alla base del tuo triangolo.
 trovare. (Per istruzioni complete sulla semplificazione delle radici quadrate, leggi questo articolo sull`argomento). Il risultato ti darà il valore della base mancante del tuo primo triangolo rettangolo. Scrivi questa lunghezza alla base del tuo triangolo.
trovare. (Per istruzioni complete sulla semplificazione delle radici quadrate, leggi questo articolo sull`argomento). Il risultato ti darà il valore della base mancante del tuo primo triangolo rettangolo. Scrivi questa lunghezza alla base del tuo triangolo.



Quindi prendi nota
 come base del primo triangolo.
come base del primo triangolo.
8. Trova la lunghezza mancante del secondo triangolo rettangolo. Per fare ciò, imposta il teorema di Pitagora per il secondo triangolo e segui i passaggi per trovare la lunghezza del lato mancante. Se stai lavorando con un trapezio isoscele (quello in cui i due lati non paralleli hanno la stessa lunghezza), allora i due triangoli rettangoli sono congruenti, quindi il valore del primo triangolo è uguale a quello del secondo triangolo.





Quindi prendi nota
 come base del secondo triangolo.
come base del secondo triangolo.
9. Somma tutte le lunghezze laterali del trapezio. Il perimetro di ogni poligono è la somma di tutti i lati:  . Per il fondo, aggiungi il lato inferiore del rettangolo, più le basi dei due triangoli. Probabilmente avrai radici quadrate nella tua risposta. Per le istruzioni complete sull`aggiunta di radici quadrate, leggi l`articolo su questo argomento. Puoi anche usare una calcolatrice per convertire le radici quadrate in decimali.
. Per il fondo, aggiungi il lato inferiore del rettangolo, più le basi dei due triangoli. Probabilmente avrai radici quadrate nella tua risposta. Per le istruzioni complete sull`aggiunta di radici quadrate, leggi l`articolo su questo argomento. Puoi anche usare una calcolatrice per convertire le radici quadrate in decimali.
 . Per il fondo, aggiungi il lato inferiore del rettangolo, più le basi dei due triangoli. Probabilmente avrai radici quadrate nella tua risposta. Per le istruzioni complete sull`aggiunta di radici quadrate, leggi l`articolo su questo argomento. Puoi anche usare una calcolatrice per convertire le radici quadrate in decimali.
. Per il fondo, aggiungi il lato inferiore del rettangolo, più le basi dei due triangoli. Probabilmente avrai radici quadrate nella tua risposta. Per le istruzioni complete sull`aggiunta di radici quadrate, leggi l`articolo su questo argomento. Puoi anche usare una calcolatrice per convertire le radici quadrate in decimali.
Dopo aver convertito le radici quadrate in decimali, hai

Quindi, la circonferenza approssimativa del tuo trapezio è 38,314 cm..
Metodo 3 di 3: Se conosci l`altezza, la lunghezza degli angoli interni superiore e inferiore

1. Dividi il trapezio in un rettangolo e due triangoli rettangoli. Per questo, indica l`altezza da entrambi gli angoli superiori.
- Se non riesci a formare due triangoli rettangoli perché un lato del trapezio è perpendicolare alla base, assicurati che questo lato abbia le stesse dimensioni dell`altezza e dividi il trapezio in un rettangolo e un triangolo rettangolo.

2. Etichetta ogni contorno. Poiché questi sono lati opposti di un rettangolo, avranno la stessa lunghezza.

3. Nota la lunghezza della parte centrale del fondo. (Questa è la parte inferiore del rettangolo.) Questa lunghezza sarà uguale alla lunghezza della parte superiore, perché i lati opposti di un rettangolo hanno la stessa lunghezza.

4. Imposta la formula del seno per il primo triangolo rettangolo. La formula è  , per cui
, per cui  l`angolo interno è,
l`angolo interno è,  l`altezza del triangolo e
l`altezza del triangolo e  è la lunghezza dell`ipotenusa.
è la lunghezza dell`ipotenusa.
 , per cui
, per cui  l`angolo interno è,
l`angolo interno è,  l`altezza del triangolo e
l`altezza del triangolo e  è la lunghezza dell`ipotenusa.
è la lunghezza dell`ipotenusa.
5. Usa i valori noti nel rapporto seno. Assicurati di utilizzare l`altezza del triangolo come lunghezza del lato opposto nella formula. lo risolvi per H.


6. Determina il seno dell`angolo. Fallo usando il pulsante SIN su una calcolatrice scientifica. Utilizzare questo valore nella formula.


7. Risolvi questo per H. Per fare ciò, moltiplica ogni lato per H, quindi dividi ogni lato per l`angolo seno. Oppure dividi l`altezza del triangolo per l`angolo seno.




Pertanto, la lunghezza dell`ipotenusa e del primo lato mancante del trapezio è di circa 10,4566 cm.

8. Trova la lunghezza dell`ipotenusa del secondo triangolo rettangolo. Imposta la formula del seno ( ) per il secondo angolo interno dato. Questo ti darà la lunghezza dell`ipotenusa, che è anche il primo lato del trapezio.
) per il secondo angolo interno dato. Questo ti darà la lunghezza dell`ipotenusa, che è anche il primo lato del trapezio.
 ) per il secondo angolo interno dato. Questo ti darà la lunghezza dell`ipotenusa, che è anche il primo lato del trapezio.
) per il secondo angolo interno dato. Questo ti darà la lunghezza dell`ipotenusa, che è anche il primo lato del trapezio.




Quindi la lunghezza dell`ipotenusa e del secondo lato mancante del trapezio è di circa 8,4854 cm.

9. Imposta il teorema di Pitagora per il primo triangolo rettangolo. Il teorema di Pitagora è forte  , dove la lunghezza dell`ipotenusa è uguale a
, dove la lunghezza dell`ipotenusa è uguale a  , e l`altezza del triangolo
, e l`altezza del triangolo  .
.
 , dove la lunghezza dell`ipotenusa è uguale a
, dove la lunghezza dell`ipotenusa è uguale a  , e l`altezza del triangolo
, e l`altezza del triangolo  .
.
10. Usa i valori noti nel teorema di Pitagora per il primo triangolo rettangolo. Assicurati di inserire il valore corretto per l`ipotenusa  e l`altezza
e l`altezza  .
.
 e l`altezza
e l`altezza  .
.

11. Risolvi questo per B  . Questo ti darà la lunghezza della base del primo triangolo rettangolo e la prima parte mancante della base del trapezio.
. Questo ti darà la lunghezza della base del primo triangolo rettangolo e la prima parte mancante della base del trapezio.
 . Questo ti darà la lunghezza della base del primo triangolo rettangolo e la prima parte mancante della base del trapezio.
. Questo ti darà la lunghezza della base del primo triangolo rettangolo e la prima parte mancante della base del trapezio.





Quindi la base del triangolo e la prima parte mancante del fondo del trapezio è di circa 8,5639 cm.

12. Trova la lunghezza della base mancante del secondo triangolo rettangolo. Usa il teorema di Pitagora ( ). Usa la lunghezza dell`ipotenusa per
). Usa la lunghezza dell`ipotenusa per  e l`altezza per
e l`altezza per  . Risolvi questo per
. Risolvi questo per  e ottieni la lunghezza della seconda parte mancante del fondo il trapezio.
e ottieni la lunghezza della seconda parte mancante del fondo il trapezio.
 ). Usa la lunghezza dell`ipotenusa per
). Usa la lunghezza dell`ipotenusa per  e l`altezza per
e l`altezza per  . Risolvi questo per
. Risolvi questo per  e ottieni la lunghezza della seconda parte mancante del fondo il trapezio.
e ottieni la lunghezza della seconda parte mancante del fondo il trapezio.





Quindi la base del secondo triangolo, e la seconda parte mancante del fondo del trapezio, è pari a 6 cm.

13. Aggiungi tutti i lati del trapezio insieme. Il perimetro di ogni poligono è la somma di tutti i lati:  . Per il fondo, aggiungi la parte inferiore del rettangolo alla base dei due triangoli.
. Per il fondo, aggiungi la parte inferiore del rettangolo alla base dei due triangoli.
 . Per il fondo, aggiungi la parte inferiore del rettangolo alla base dei due triangoli.
. Per il fondo, aggiungi la parte inferiore del rettangolo alla base dei due triangoli.
Quindi la circonferenza approssimativa del trapezio è 45,5059 cm.
Consigli
- Usa le leggi dei triangoli speciali per trovare le lunghezze mancanti dei triangoli speciali, senza usare la formula del seno o il teorema di Pitagora. Le leggi si applicano a un triangolo 30-60-90 o a un triangolo 90-45-45.
- Utilizzare una calcolatrice scientifica per determinare il seno di un angolo, inserendo l`angolo e quindi premendo il pulsante `SIN`. Puoi anche usare una tavola trigonometrica.
Necessità
- Calcolatrice
- Matita
- Carta
Articoli sull'argomento "Calcolo del perimetro di un trapezio"
Condividi sui social network:
Simile
Popolare