Ora stai lavorando su un triangolo equilatero perché tutti e tre i lati della figura hanno esattamente la stessa lunghezza. Ma ricorda che questa formula si applica a tutti i triangoli. 
Altro esempio: Se a = 4, b = 3, e c=5, allora la circonferenza è 3+4+5, in altre parole 12. 
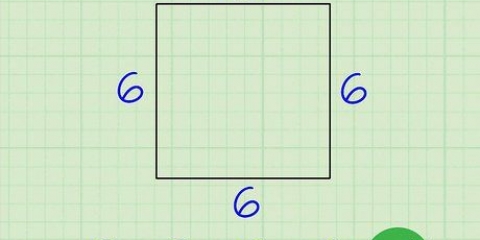
In questo esempio, i lati sono tutti 5 cm, quindi la risposta corretta è 15 cm. 



Ad esempio, se conosci quella seta a = 3 e seta b = 4, quindi scrivilo nella formula in questo modo: 3 + 4 = c. Un secondo esempio: se sai che la lunghezza del latoa = 6, e l`ipotenusa c = 10, quindi lo metti nell`equazione in questo modo: 6 + b = 10. 
Nel primo esempio moltiplichi i valori in 3 + 4 = c e lo scopri e 25= c. Quindi calcola la radice quadrata di 25 in modo da arrivare a c = 25. Nel secondo esempio moltiplichi i valori in 6 + b = 10 e lo scopri 36 + b = 100.Sottrarre 36 da 100 per ottenere b = 64, e poi calcola la radice quadrata di 64, in modo da ottenere b = 8. 
Nel primo esempio che è X = 3 + 4 + 5 o 12. Nel secondo esempio, cioè X = 6 + 8 + 10 o 24. 

Ad esempio, immagina un triangolo con un lato di 10 e uno di 12 e un angolo di 97° tra di loro. Scriviamo quindi le variabili come segue:a = 10, b = 12, C = 97°. 
c = 10 + 12 - 2 × 10 × 12 × cos(97). c = 100 + 144 – (240 × -0,12187)(Arrotonda il coseno a 5 cifre dopo la virgola) c = 244 – (-29,25) c = 244 + 29,25(Prendi il segno meno se cos(C) è negativo!) c = 273,25 c = 16.53 
Nel nostro esempio: 10 + 12 + 16.53 = 38.53, questo è il perimetro del nostro triangolo!
Calcolo del perimetro di un triangolo
Contenuto
Il perimetro di un triangolo è la lunghezza di una linea che può essere tracciata lungo i lati del triangolo. Il modo più semplice è sommare le lunghezze di tutti i lati, ma se non conosci tutte le lunghezze devi prima calcolarle. Questo articolo ti insegna innanzitutto come calcolare il perimetro di un triangolo se conosci le lunghezze di tutti e tre i lati; questo è il metodo più semplice e più utilizzato. Quindi imparerai a calcolare il perimetro se conosci solo le lunghezze di due dei tre lati. Infine, spiega come calcolare il perimetro se conosci le lunghezze di due lati e l`angolo tra di loro, usando la legge dei coseni.
Passi
Metodo 1 di 3: Calcolare il perimetro di un triangolo se sono fornite le lunghezze di tutti i lati

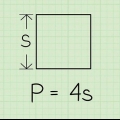
1. Impara la formula per trovare il perimetro. La formula è: A + B + C = X per cui un, B, e C rappresentano le lunghezze dei lati e X la circonferenza.
- Questa formula in pratica significa che per trovare il perimetro di un triangolo, devi sommare le lunghezze dei tre lati.

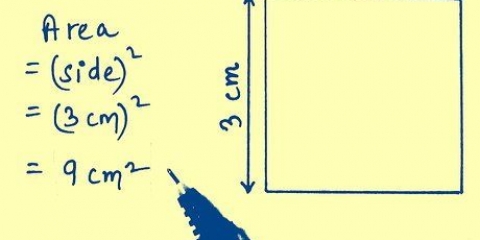
2. Determina le lunghezze di tutti e tre i lati. In questo esempio: un = 5, B = 5, C = 5.

3. Aggiungi le lunghezze dei tre lati insieme. In questo esempio: 5 + 5 + 5 = 15. Quindi il perimetro del triangolo (X) è 15.

4. Ricorda di includere sempre le unità nella tua risposta. Se i lati sono espressi in centimetri, anche la tua risposta finale deve essere espressa in centimetri. Se i lati sono dati in termini di una variabile, ad esempio x, anche la risposta deve essere in termini di x.
Metodo 2 di 3: Calcolo del perimetro se sono dati solo due lati del triangolo

1. Scopri cos`è un triangolo rettangolo. Un triangolo rettangolo è un triangolo con un angolo retto (90 gradi). Il lato del triangolo opposto all`angolo retto è sempre il lato più lungo, chiamato ipotenusa o ipotenusa. I triangoli ad angolo retto spuntano regolarmente nei test di matematica, ma fortunatamente esiste una formula molto utile per calcolare la lunghezza del lato sconosciuto!

2. Conosci il teorema di Pitagora. Il teorema di Pitagora si applica a qualsiasi triangolo rettangolo e si legge: a² + b² = c².

3. Guarda il tuo triangolo e scrivi ai lati un, B e C. Ricorda che il lato più lungo è chiamato ipotenusa. Si trova di fronte all`angolo retto e devi andare da questo lato C scrivere. Ai due lati più corti scrivi un e B. Non importa quale metti dove, il risultato sarà lo stesso!

4. Prendi le lunghezze dei lati nel teorema di Pitagora. Ricordati che a + b = c. Inserisci le lunghezze al posto delle lettere corrispondenti.

5. Risolvi l`equazione per trovare la lunghezza mancante. Devi prima moltiplicare i lati conosciuti per loro stessi (ad esempio, 3 = 3 * 3 = 9).Se stai cercando l`ipotenusa, puoi semplicemente sommare i due valori e calcolare la radice quadrata del risultato per trovare la lunghezza. Se ti manca un altro lato devi sottrarre i due e poi calcolare la radice quadrata del risultato per trovare la lunghezza.

6. Somma le lunghezze dei tre lati per calcolare il perimetro. Ricorda l`equazione: X = a + b + c. Ora che conosci le lunghezze dei latiun, B e C sappi che puoi sommarli insieme per ottenere la circonferenza.
Metodo 3 di 3: Trovare il perimetro di un triangolo usando la legge dei coseni

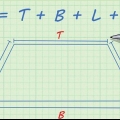
1. Impara la legge dei coseni. Usando la legge dei coseni, puoi risolvere qualsiasi triangolo se conosci le lunghezze di due lati e l`angolo tra di loro. Funziona per qualsiasi triangolo ed è una formula molto utile. La legge dei coseni afferma che, per ogni triangolo con lati un, B, e C, con angoli oppostiun, B, e C vale la seguente formula:c = a + b - 2ab cos(C).

2. Guarda il tuo triangolo e metti le lettere nelle diverse parti. La prima parte che sai che devi un chiamalo, e allora c`è l`angolo opposto un. Il secondo lato che sai che devi B chiama l`angolo opposto B. L`angolo che sai che devi C chiamalo, e il terzo lato, quello che vuoi risolvere, è quindi C.

3. Inserisci le tue informazioni nell`equazione e risolvi per il lato c. Devi prima moltiplicare aeb per loro stessi e sommarli. Quindi calcola il coseno di C con il cos-funzione sulla calcolatrice o su una calcolatrice online. Moltiplicare cos(C) di 2ab e sottrarre il risultato dalla somma di a + b.La risposta è C.Calcola la radice quadrata di questo e conosci la lunghezza del lato C.Nel nostro esempio:

4. Usa la lunghezza diC per calcolare il perimetro del tuo triangolo. Ricorda che la formula per la circonferenza è: X = a + b + c, quindi devi solo sommare tutte le lunghezze perché un e B Lo sapevate.Pezzo di torta!
Articoli sull'argomento "Calcolo del perimetro di un triangolo"
Condividi sui social network:
Popolare