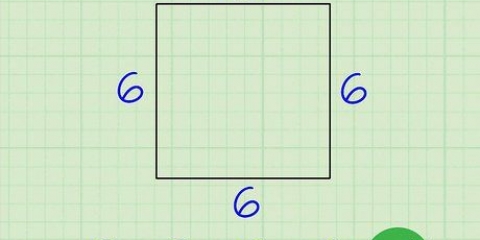
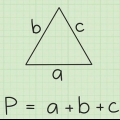Se il quadrato ha un lato di lunghezza 4:Circonferenza = 4 * 4, in altre parole 16. Se il quadrato ha un lato di lunghezza 6: Circonferenza = 4 * 6, in altre parole 24. 

Se l`area del quadrato è 20, allora lo è la lunghezza del lato S: =√20 o 4.472 Se l`area del quadrato è 25, allora lo è la lunghezza del lato s = √25 o 5. 
Per un quadrato di area 20 e lato 4.473, il perimetro è: Circonferenza = 4 * 4,472 o 17.888. Per un quadrato di area 25 e lato 5, il perimetro è: Circonferenza = 4 * 5 o 20. 


a + a = (2r), ora possiamo semplificare: 2a = 4(r), ora dividi entrambi i membri per 2: (a) = 2(r), ora prendi la radice quadrata di ogni lato: a = √(2)r.La nostra lunghezza di un lato S del quadrato inscritto = √(2)r. 

Nota: potevi farlo anche in questo modo: moltiplica il raggio (10) per il numero 5.567. 10*5.567 = 56.57, ma poiché potrebbe essere difficile da ricordare, è meglio che attraversi l`intero processo.
Calcolo del perimetro di un quadrato
Contenuto
Il perimetro di una figura bidimensionale è la distanza totale attorno alla figura, ovvero la somma delle lunghezze dei lati. La definizione di quadrato è una figura con quattro lati uguali e quattro angoli retti (90°) tra quei lati. Poiché tutti i lati hanno la stessa lunghezza, è molto facile determinare il perimetro di un quadrato! Questo articolo spiega innanzitutto come calcolare il perimetro di un quadrato se conosci la lunghezza di uno dei suoi lati. Quindi ti mostreremo come calcolare il perimetro se conosci solo l`area e nell`ultima sezione ti insegneremo come calcolare il perimetro di un quadrato inscritto in un cerchio di cui è nota la lunghezza del raggio.
Passi
Metodo 1 di 3: Trovare il perimetro di un quadrato se conosci la lunghezza di un lato

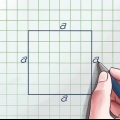
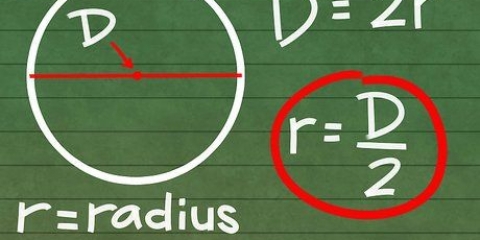
1. Pensa alla formula per il perimetro di un quadrato. Per un quadrato dove troviamo la lunghezza del lato S il perimetro è semplicemente quattro volte la lunghezza di quel lato: Circonferenza = 4 s (nota: nelle immagini la lettera P è usata per il contorno, dall`inglese `Perimeter`).

2. Trova la lunghezza di un lato e moltiplicala per 4 per trovare il perimetro. A seconda del compito, potrebbe essere necessario misurare con un righello o guardare altre informazioni per determinare la lunghezza di un lato. Ecco alcuni esempi di calcolo della circonferenza:
Metodo 2 di 3: Determinare il perimetro di un quadrato se ne conosci l`area

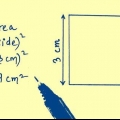
1. Conosci la formula per l`area di un quadrato. L`area di qualsiasi rettangolo (ricordate che i quadrati sono rettangoli speciali) può essere definita come base per altezza.Poiché base e altezza sono uguali nel caso di un quadrato, l`area di un quadrato con lato S: s*s. In altre parole: area = s.

2. Prendi la radice quadrata dell`area. La radice quadrata dell`area ti dà la lunghezza di uno dei lati del quadrato. Per la maggior parte dei numeri è necessaria una calcolatrice per calcolare la radice quadrata. Digitare prima il numero, quindi premere il tasto radice quadrata (√).

3. Moltiplica la lunghezza del lato per 4 per trovare la circonferenza. Usa il valore della lunghezza del lato che hai appena trovato nella formula Circonferenza = 4 s. Il risultato è il perimetro del tuo quadrato!
Metodo 3 di 3: Calcolare il perimetro di un quadrato inscritto in un cerchio se conosci il raggio

1. Comprendi cos`è un quadrato inscritto. Un quadrato inscritto in un cerchio è un quadrato disegnato in un cerchio con tutti gli angoli del quadrato che toccano il cerchio.

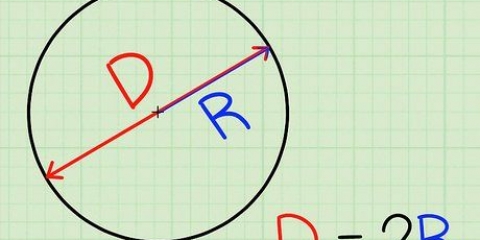
2. Comprendere la relazione tra il raggio del cerchio e la lunghezza dei lati del quadrato. La distanza dal centro di un quadrato inscritto a qualsiasi angolo è uguale al raggio del cerchio. Alla lunghezza laterale S per trovarlo, dobbiamo prima immaginare di tagliare il quadrato a metà in diagonale, in modo da formare due triangoli equilateri. Questi triangoli hanno lati uguali un e B e un`ipotenusa C, che sappiamo essere uguale al doppio del raggio del cerchio, cioè 2r.

3. Usa il teorema di Pitagora per trovare la lunghezza del lato del quadrato. Il teorema di Pitagora è il seguente: in un triangolo rettangolo, la somma dei quadrati delle lunghezze dei lati rettangolari (a,b) è uguale al quadrato della lunghezza dell`ipotenusa (c), a + b = c. Perché i lati un e B sono uguali (siamo ancora a che fare con un quadrato!) e lo sappiamo c=2r ora possiamo scrivere l`equazione e semplificarla per trovare la lunghezza di un lato:

4. Moltiplica la lunghezza di un lato del quadrato per quattro per trovare il perimetro. In questo caso il perimetro del quadrato è: Circonferenza = 4√(2)r. La circonferenza di un quadrato inscritto in una circonferenza è quindi sempre uguale a 4√(2)r, ovvero circa 5,657r

5. Risolvi una domanda di esempio. Prendiamo un quadrato inscritto in una circonferenza di raggio 10. Ciò significa che la diagonale del quadrato = 2(10) o 20. Il teorema di Pitagora ci insegna che: 2(a) = 20, Così 2a = 400. Ora dividi entrambi i lati per due, lo vediamo a = 200. Prendi la radice quadrata di ciascun lato e lo vediamo a = 14.142. Moltiplica questo per 4 per trovare il perimetro del tuo quadrato: Circonferenza = 56,57.
Articoli sull'argomento "Calcolo del perimetro di un quadrato"
Condividi sui social network:
Popolare